1. he time constant of a series RC circuit (τ) is given by
a) R/C
b) C/R
c) RC
d) 1/RC
Explanation: For a series RC circuit, τ = RC.
2. A circuit is so formed such that source-R-L-diode-switch are all in series. Consider the initial current in L to be zero. The diode is so connected that it is forward biased when switch is closed.
When the switch is closed,
a) the current will decay exponentially & the voltage will increase exponentially
b) the current will increase exponentially & the voltage will decay exponentially
c) the current will fall to zero & the voltage both will decay exponentially
d) the voltage and the current both remain constant
Explanation: Instant switch is closed, the current is minimum zero than starts to increase till it reaches a constant value Vs/R, whereas voltage starts to reduce from Vs to 0 (Inductor Charging).
3. For a diode circuit the voltage across the capacitor is given by
Vc(t)= Vs(1-e(-t/RC))
Then the initial rate of change of capacitor voltage is given by
a) 0
b) ∞
c) Vs x RC
d) Vs/RC
Explanation: Find d(Vc)/dt and put t = 0.
4. The time constant of a series RL circuit (τ) is given by
a) R/L
b) L/R
c) RC
d) 1/RL
Explanation: The time constant τ for a series RL circuit is R/L.
5. For the initially relaxed circuit shown below, KVL with switch in the closed position gives a certain equation. The Laplace of this equation will have the right hand side (RHS) as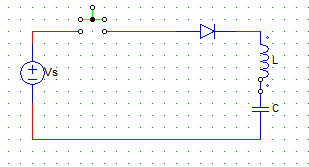
a) Vs
b) (Vs x s)/RC
c) Vs/s
d) RC/s
Explanation: When switch is closed,
Ldi/dt + 1/C ∫ idt = Vs
Laplace of the above gives,
L[sI(s)] + 1/C [I(s)/s] = Vs/s.
6. For the initially relaxed circuit shown below, the Laplace transform of the KVL when the switch is closed is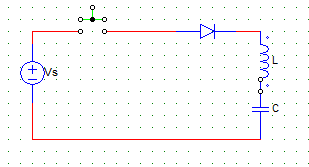
I(s) [ X ] = Vs/s
The value of X is
a) sL + 1/C
b) Cs + 1/sL
c) sL + 1/sC
d) Vs/CLs
Explanation: When switch is closed,
Ldi/dt + 1/C ∫ idt = Vs
Laplace of the above gives,
L[sI(s)] + 1/C [I(s)/s] = Vs/s.
7. For the initially relaxed circuit shown below, if Ω=1/√LC. Then the current is a function of ___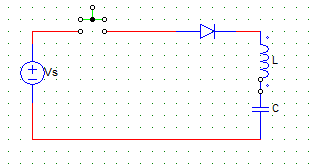
a) cos Ωt
b) sin Ωt
c) tan Ωt
d) cos Ωt.sin Ωt
Explanation: When switch is closed,
Ldi/dt + 1/C ∫ idt = Vs
Laplace of the above gives,
L[sI(s)] + 1/C [I(s)/s] = Vs/s
I(s) = Vs/(LΩ) * (Ω/Ω2 + s2)
Taking the inverse lapace gives,
I(t) = Vs * √ (L/C) * sin Ωt.
8. For the circuit shown below, the capacitor is initially charged to a voltage of Vo with the upper plate positive. After the switch (shown in green) is closed, the current through the load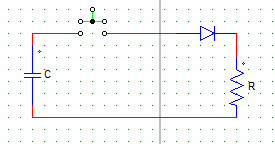
a) increases from zero to Vo/R
b) decreases from Vo/R to zero
c) increases from zero to Vo/C
d) decreases from Vo/C to zero
Explanation:The capacitor acts as a source. At instant switch is closed the current is maximum and than discharges till zero value through the load R.
9. For the circuit shown below, the capacitor is initially charged to a voltage of Vo with the upper plate positive. Switch is closed at t=0. The peak value of the current through the diode is
a) Vo/C
b) Vo/R
c) Vo
d) Vo/(RC)
Explanation: When switch is closed, the equation is
Ri + 1/C ∫idt = 0 (Voltage across capacitor cannot change instantaneously)
Solution of the above equation gives, Vo/R at t= 0.
10. When the switch (shown in green) is closed, the average current through the diode in the positive cycle is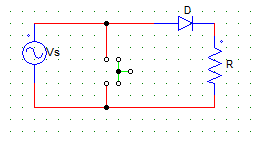
a) 0
b) Vs/R
c) Vs/(R+Rd)
d) none of the mentioned
Explanation: The switch S.C’s the source.