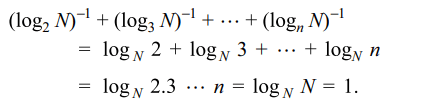1. If \[S_{n}=\sum_{r=1}^{n} t_{r}=\frac{1}{6}n\left(n+1\right)\left(n+2\right) \forall n\geq 1\]
then
\[\lim_{n \rightarrow \infty}\sum_{r=1}^{n} \frac{1}{t_{r}}\] is
a) 1
b) 3/2
c) 2
d) 5/2
Explanation:
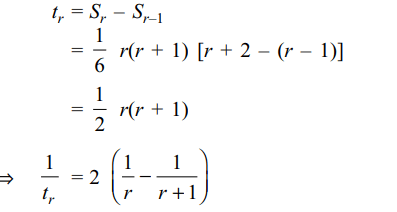
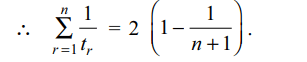
2. If unit’s digit of \[1^{2}+2^{2}+....+n^{2}\] is 5, then unit’s
digit of \[1^{10}+2^{10}+....+n^{10}\] is
a) 1
b) 3
c) 5
d) 7
Explanation: Use the fact that n10 and n2 have the same unit’s digit
3. Four geometric means are inserted between \[2^{11}-1\]
and \[2^{11}+1\] . The product of these geometric means
is
a) \[2^{44}-1\]
b) \[2^{44}-2^{23}+1\]
c) \[2^{44}-2^{22}+1\]
d) \[2^{45}-1\]
Explanation:
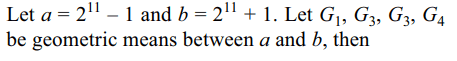
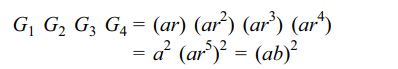
4. Let \[S_{n}=\frac{1}{2^{2}-1}+\frac{1}{4^{2}-1}+....+\frac{1}{\left(2n\right)^{2}-1}\] then value
of \[S_{25}\] is
a) 25/54
b) 25/53
c) 25/51
d) 1/2
Explanation:
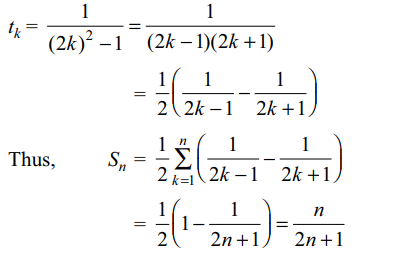
5. Suppose \[t_{r}=1^{2}+2^{2}+....+r^{2}\] . Let
\[t_{1}+t_{2}+....+t_{n}=\frac{1}{12}n\left(n+1\right)\left(n+2\right)k\]
then value of k is
a) n+1
b) 2n+1
c) 3n-1
d) n
Explanation:
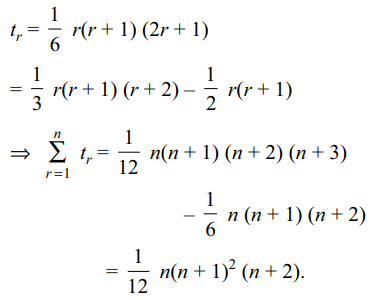
6. Let a, b, c > 0 and a, b, c be in A.P. If \[a^{2},b^{2},c^{2}\] are
in G.P., then
a) a = b = c
b) \[a^{2}+b^{2}=c^{2}\]
c) \[a^{2}+c^{2}=3b^{2}\]
d) none of these
Explanation: Use a, b, c are in G.P
7. Sum of the infinite series \[\frac{1}{3}+\frac{3}{\left(3\right)\left(7\right)}+\frac{5}{\left(3\right)\left(7\right)\left(11\right)}+\frac{7}{\left(3\right)\left(7\right)\left(11\right)\left(15\right)}+....\]
is
a) 1/2
b) 1/3
c) 1/6
d) 1/4
Explanation:
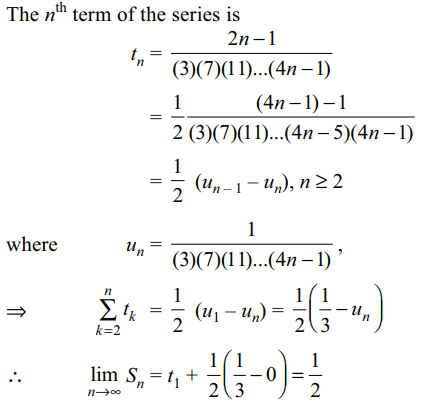
8. Let S = \[\frac{4}{19}+\frac{44}{19^{2}}+\frac{444}{19^{3}}+.... \infty\]
Then S is equal to
a) 40/9
b) 38/81
c) 36/171
d) none of these
Explanation:

9. If a, b, c, ... are in G.P., and \[a^{1/x}=b^{1/y}=c^{1/z}...,\] , then
x, y, z, ... are in
a) H.P
b) G.P
c) A.P
d) none of these
Explanation:
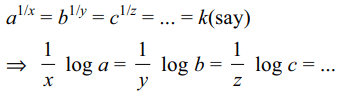
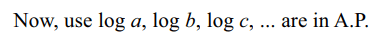
10. If \[a^{x}=b^{y}=c^{z}=d^{u}\] and a, b, c, d are in G.P., then
x, y, z, u are in
a) A.P
b) G.P
c) H.P
d) none of these
Explanation: H.P
11. Let N = 2 + 22 + 222 + ... upto 30000 terms.
a) last digit of N is 0
b) last four digits of N are 580
c) last four digits of N are 9580
d) All of the Above
Explanation:

12. Let \[\left(1+x\right)^{2}\left(1+\frac{x}{2}\right)^{2}\left(1+\frac{x}{2^{2}}\right)^{2}\left(1+\frac{x}{2^{3}}\right)^{2}... \infty\]
\[=a_{0}+a_{1}x+a_{2}x_{2}+... \infty\]
then
a) \[a_{1}=4\]
b) \[a_{2}=20/3\]
c) \[a_{2}=16/3\]
d) Both a and b
Explanation:

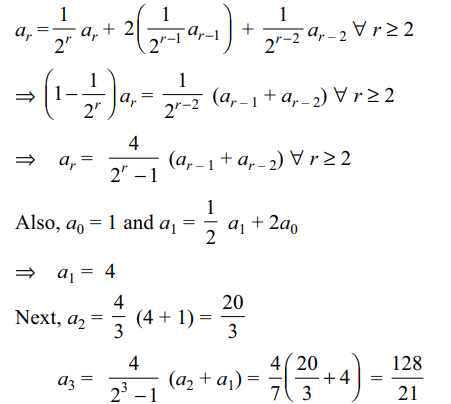
13. If a, b, c, d are in G.P., then value of
\[\left(a – c\right)^{2} + \left(c – b\right)^{2} + \left(b – d\right)^{2} –\left(d – a\right)^{2}\]
is independent of
a) a
b) b
c) c
d) All of the Above
Explanation: Let common ratio be r. Given expression equals
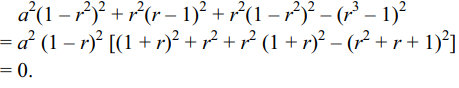
14. If sum of the infinite G.P. p, 1, 1/p, 1/p2, .... is 9/2, then value of then value of p is
a) 2
b) 3/2
c) 3
d) Both b and c
Explanation:
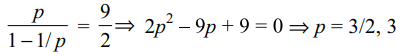
15. If a, b, c are in A.P., and \[a^{2} , b^{2} , c^{2} \] are in H.P., then
a) a = b = c
b) – a, 2b, 2c are in G.P.
c) a, b, c are in G.P.
d) All of the Above
Explanation:

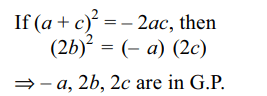
16. Let \[\log x=\log_{10}x\forall x>0\]
suppose x,y,z>1, then least value of
\[E=\log\left(xyz\right)=\left[\frac{\log x}{\log y \log z}+\frac{\log y}{\log z \log x}+\frac{\log z}{\log x \log y}\right]\]
is
a) 3
b) 6
c) 9
d) 18
Explanation:
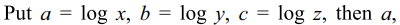
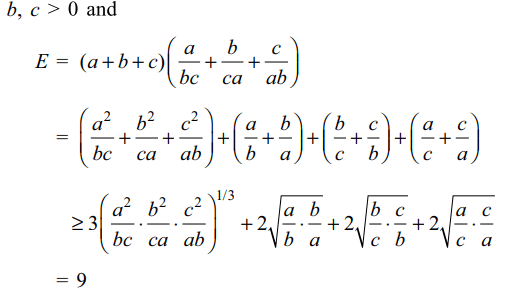
17. Number of solution of \[e\log_{e}x=x\]
is
a) 0
b) 1
c) 2
d) infinite
Explanation: It is defined for x > 0
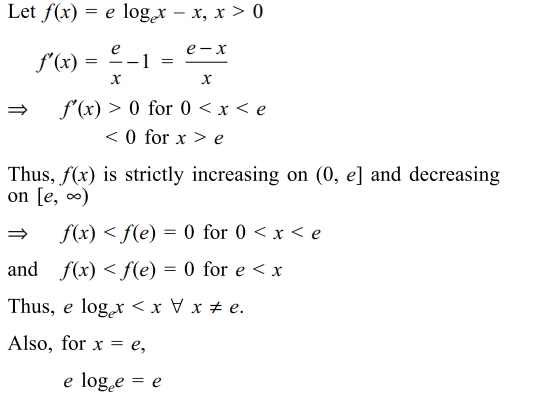
It has exactly one solution
18. If a,b \[\geq\] 1, a+b=10 ,then minimum value of \[\log_{3}a+\log_{3}b\] is
a) 2
b) \[2\log_{3}5\]
c) \[\frac{1}{2}\log_{3}5\]
d) 1
Explanation:
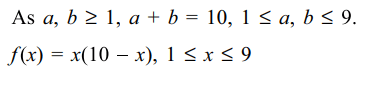
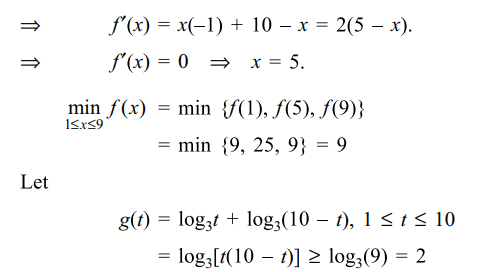
19. If \[5^{x}=7^{x+1}\] , then x is equal to
a) \[\frac{1}{\log_{5}7+1}\]
b) \[\frac{1}{\log_{7}5-1}\]
c) \[\log_{7}5\]
d) \[\log_{5}7\]
Explanation:
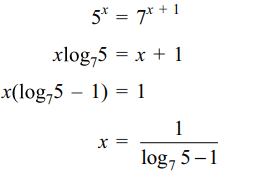
20. Let \[\left(x_{0},y_{0}\right)\] be the solution of the following system of equations
\[\left(2x\right)^{ln2}=\left(3y\right)^{ln3}\]
\[3^{lnx}=2^{lny}\]
then \[x_{0}\] is equals to
a) 1/6
b) 1/3
c) 1/2
d) 2
Explanation:
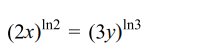
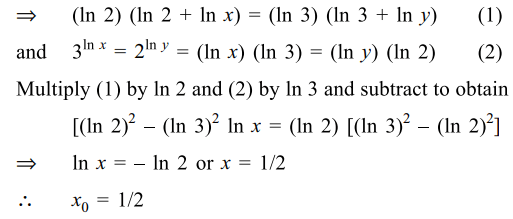
21. Solutons set of the inequality \[\log_{x}\left(2x^{2}+x-1\right)>\log_{x}\left(2\right)-1\]
is
a) \[\left(1/2 ,1\right)\]
b) \[\left(1/2 ,1\right)\cup\left(1,\infty\right)\]
c) \[\left(1,\infty\right)\]
d) \[\left(0,1\right)\]
Explanation: It holds for 1/2 < x < 1, x > 1
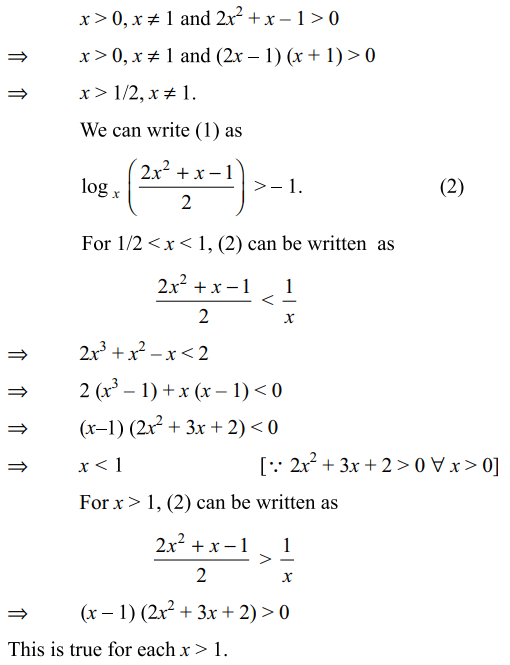
22. The value of of x stisfying \[\log_{2}\left(3x-2\right)=\log_{1/2}x\]
is
a) -1/3
b) 2
c) 1/2
d) 1
Explanation:
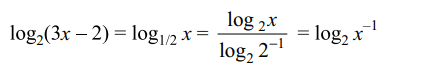

23. The solutions of the equations \[4^{\log_{2}\log x}=\log x-\left(\log x\right)^{2}+1\]
is
a) x = 1
b) x = 4
c) x = e
d) \[x = e^{2}\]
Explanation:
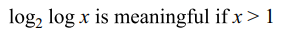
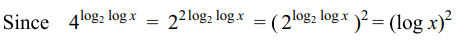
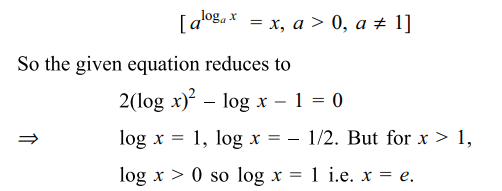
24. The set of all x satisfying the equations \[x^{\log_{3}x^{2}+\left(\log_{3} x\right)^{2}-10} =1/x^{2}\]
is
a) \[\left\{ 1,9\right\}\]
b) \[\left\{ 1,9,1/81\right\}\]
c) \[\left\{ 1,4, 1/81\right\}\]
d) \[\left\{ 9,1/81 \right\}\]
Explanation: Taking log of both the sides with base 3, we have
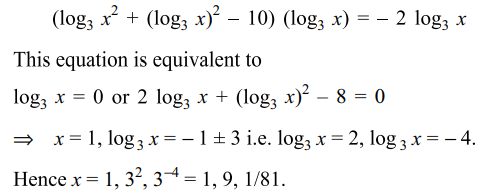
25.The set of all solutions of the inequality \[\left(1/2\right)^{x^{2}-2x}< 1/4\] contains the sets
a) \[\left(-\infty ,0\right)\]
b) \[\left(-\infty ,1\right)\]
c) \[\left(1,\infty \right)\]
d) \[\left(3,\infty \right)\]
Explanation:

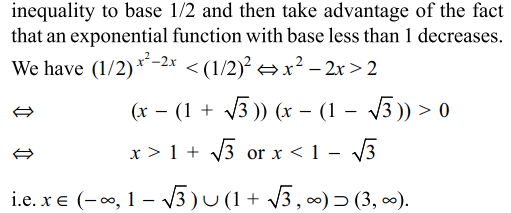
26. The set of all the solutions of the inequality \[\log_{1-x}\left(x-2\right)\geq -1\] is
a) \[\left(-\infty ,0\right)\]
b) \[\left(2,\infty \right)\]
c) \[\left(-\infty ,1\right)\]
d) \[\phi\]
Explanation:
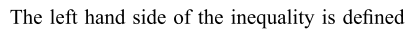

27. If \[\log_{3}x+\log_{3}y = 2+\log_{3}2\] and \[\log_{3}\left(x+y\right)=2\] then
a) x = 1, y = 8
b) x = 8, y = 1
c) x = 3, y = 6
d) x = 9, y = 3
Explanation:
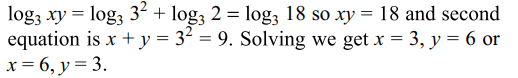
28. The set of all solutions of the equations \[\log_{3}x\log_{4}x\log_{5}x=\log_{3}x\log_{4}x+\log_{4}x\log_{5}x+\log_{5}x\log_{3}x\]
is
a) {1}
b) {1,60}
c) {1,5,10,60}
d) {1,4,8,60}
Explanation:
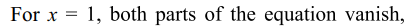
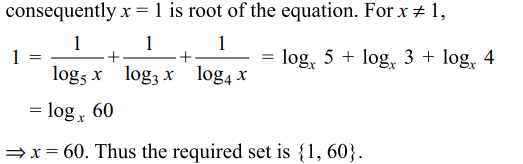
29. If \[\log_{30}3=c,\log_{30}5=d\] then the value of \[\log_{30}8\]
a) 2(1-c-d)
b) 3(1+c+d)
c) 3(1+c-d)
d) 3(1-c-d)
Explanation:
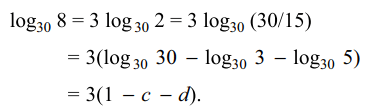
30. if \[a=\log_{12}18,b=\log_{24}54\] then the value of ab+5(a-b) is
a) 0
b) 4
c) 1
d) 8
Explanation:
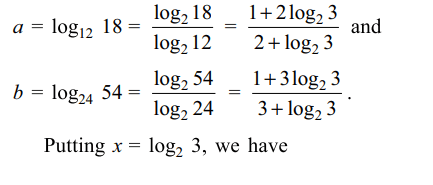

31. The value of \[\frac{\log_{2}24}{\log_{96}2}-\frac{\log_{2}192}{\log_{12}2}\]
is
a) 3
b) 0
c) 2
d) 1
Explanation:
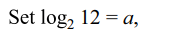
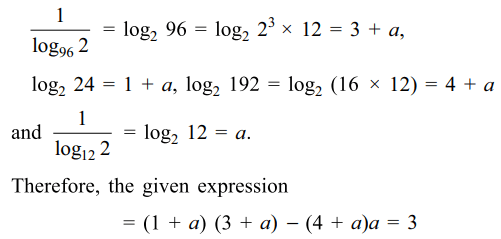
32. The set of all value of x satisfying \[x^{\log_{x}\left(1-x\right)^{2}}=9\]
is
a) a subset of R containing N
b) a subset of R containing 1
c) is a finite set containg at least two elements
d) a finite set .
Explanation: Note that x > 0, x \[\neq\] 1
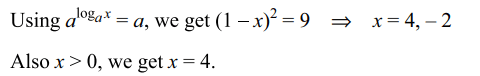
33. The set \[\left\{x: \mid 1-\log_{1/5}x\mid +2=\mid 3-\log_{1/5}x\mid\right\}\] is equal to
a) \[\left( 0,\infty\right)\]
b) \[\left[ 1/5,\infty\right)\]
c) \[\left[ 1/5,5\right)\]
d) \[\left(0,1/5\right]\]
Explanation:
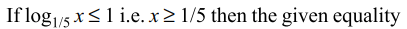
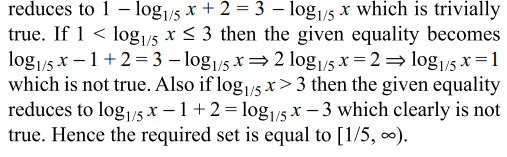
34. The set of \[\left\{x: \log_{1/3}\log_{4}\left(x^{2}-5\right)>0\right\}\] is equal to
a) \[\left(3,\infty\right)\]
b) \[\left(\sqrt{6},3\right)\]
c) \[\left(-3,-\sqrt{6}\right)\cup\left(\sqrt{6},3\right)\]
d) \[\left(\sqrt{6},\infty\right)\]
Explanation:
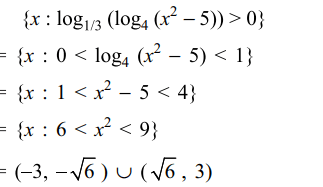
35. The number of solutions of \[\log_{4}\left(x-1\right)=\log_{2}\left(x-3\right)\]
is
a) 3
b) 1
c) 2
d) 0
Explanation:

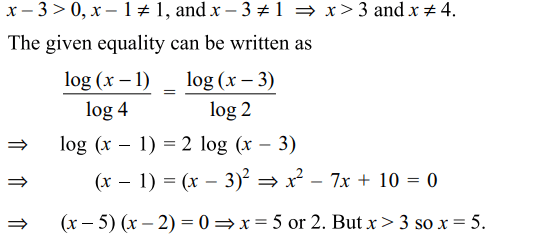
36. Solutions set of the inequality
\[\log_{3}\left(x+2\right)\left(x+4\right)+\log_{1/3}\left(x+2\right)<\frac{1}{2}\log_{\sqrt{3}}7\]
is
a) \[\left(-2,-1\right)\]
b) \[\left(-2,3\right)\]
c) \[\left(-1,3\right)\]
d) \[\left(3,\infty\right)\]
Explanation:
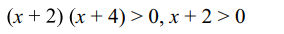
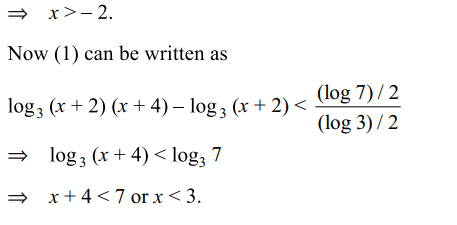
37. The solution set of \[\log_{\mid\sin x\mid}\left(x^{2}-8x+23\right)>\frac{3}{\log_2{\mid\sin x\mid}}\] contains
a) \[x\epsilon \left(3,\pi\right)\cup\left(\pi,\frac{3\pi}{2}\right)\cup\left(\frac{3\pi}{2},5\right)\]
b) \[x\epsilon \left(3,\pi\right)\cup\left(\pi,5\right)\]
c) \[x\epsilon \left(3,\frac{5\pi}{2}\right)\]
d) \[x\epsilon \left(2,5\pi/2\right)\]
Explanation:
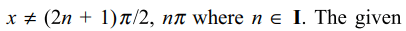
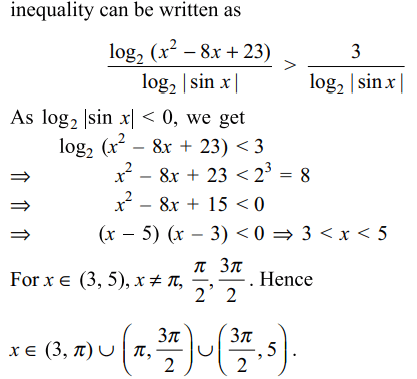
38. If n>1, the value of \[\frac{1}{\log_{2}n}+\frac{1}{\log_{3}n}+....+\frac{1}{\log_{53}n}\]
is
a) \[\frac{1}{\log_{53!}n}\]
b) 1
c) \[\frac{1}{\log_{n!}53}\]
d) \[\frac{1}{53}\]
Explanation:
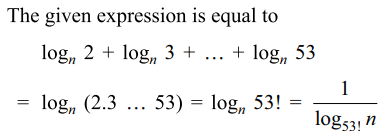
39. The number of values of \[x \epsilon \left[0,n\pi\right],n \epsilon I\] that satisfy
\[\log_{\mid \sin x\mid}\left(1+\cos x\right)=2\] is
a) 0
b) n
c) 2n
d) 1
Explanation:
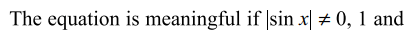
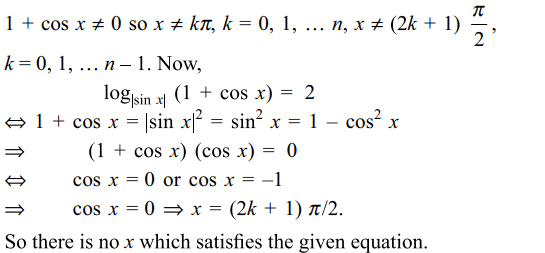
40. Let \[\triangle=\begin{bmatrix}\log \left(7/15\right) & \log \left(49\right) & \log \left(49\right) \\\log \left(25\right) &\log \left(5/21\right) & \log \left(25\right) \\\log \left(9\right) & \log \left(9\right) &\log \left(3/35\right)\end{bmatrix}\]
then \[\triangle\] is equal to
a) \[\left(\log \left(105\right)\right)^{2}\]
b) \[\left(\log \left(105\right)\right)^{3}\]
c) \[\left(\log \left(35/3\right)\right)^{3}\]
d) \[\left(\log \left(21/5\right)\right)^{3}\]
Explanation:
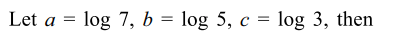
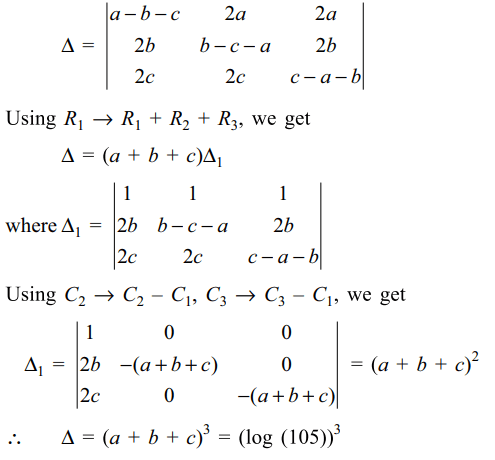
41. Suppose p,q,r,\[s\epsilon N\] and \[p\geq q\geq r\] . If \[5^{\log_{5}\left(2^{p}\right)}+7^{\log_{7}\left(2^{q}\right)}+11^{\log_{11}\left(2^{r}\right)}=2^{s}\]
a) q=p-1
b) r=p-1
c) s=p+1
d) All of the Above
Explanation: As for a > 0, a \[\neq\] 1,
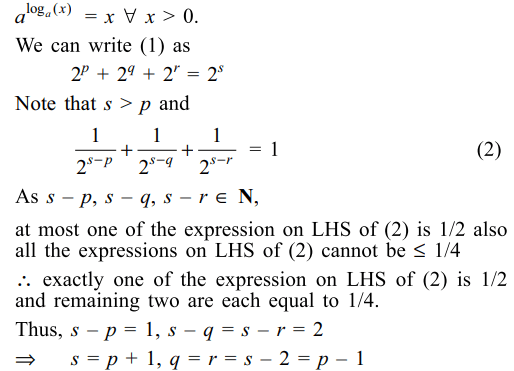
42. Suppose a,b,c,\[d\epsilon \left(1,\infty\right)\] and let
\[\alpha =\log_{abc}\left(10\right)+\log_{acd}\left(10\right)+\log_{abd}\left(10\right)+\log_{bcd }\left(10\right)\]
and \[\beta =\log_{a}\left(10\right)+\log_{b}\left(10\right)+\log_{c}\left(10\right)+\log_{d }\left(10\right)\]
a) \[\alpha\leq\beta\]
b) \[2\alpha\leq\beta\]
c) \[3\alpha\leq\beta\]
d) All of the Above
Explanation:
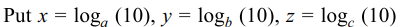
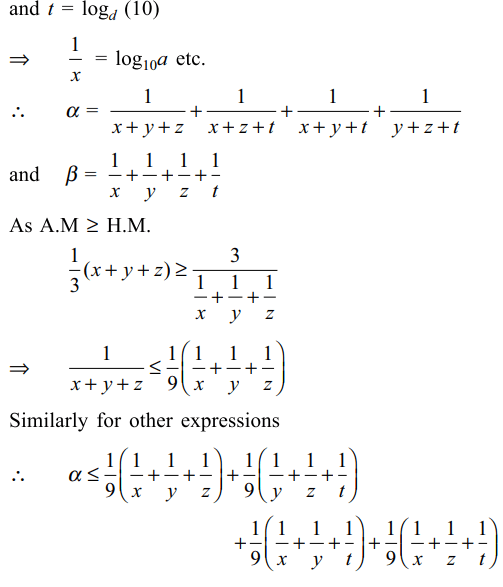
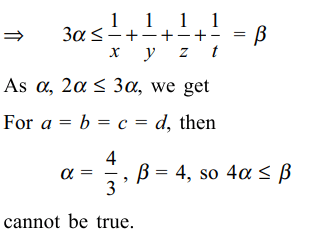
43. The set of all x satisfying \[4^{x^{2}+2}-\left(9\right)2^{x^{2}+2}+8=0\]
consists of
a) infinitely many points
b) exactly two integers
c) finitely many points from the set of all integers
d) Both b and c
Explanation:
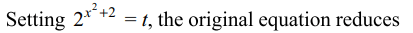
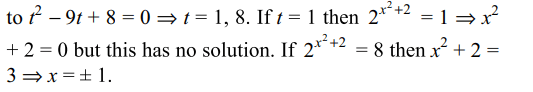
44. The equations \[x^{\left[\left(\log_{5}x\right)^{2}-\frac{9}{2}\log_{5}x+5\right]}=5\sqrt{5}\]
has
a) exactly three real solution
b) at least one real solution
c) exactly one irrational solution
d) All of the Above
Explanation: Taking logarithm of both sides, we get
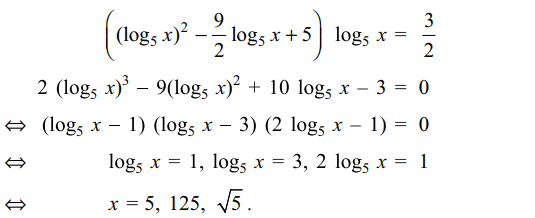
45. if \[\log_{2}\left(3^{2x-2}+7\right)=2+\log_{2}\left(3^{x-1}+1\right)\]
then x equals
a) 0
b) 1
c) 2
d) Both b and c
Explanation:
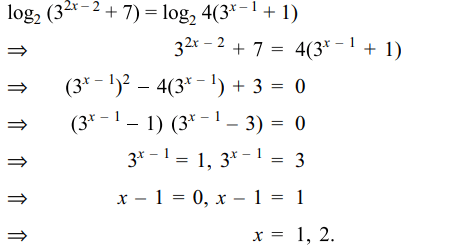
46. Solution of \[\log_{x^{2}+6x+8}\log_{2x^{2}+2x+3}\left(x^{2}-2x\right)=0\]
is
a) a natural number
b) a negative integer
c) -1
d) Both b and c
Explanation:
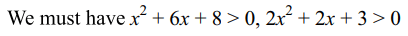
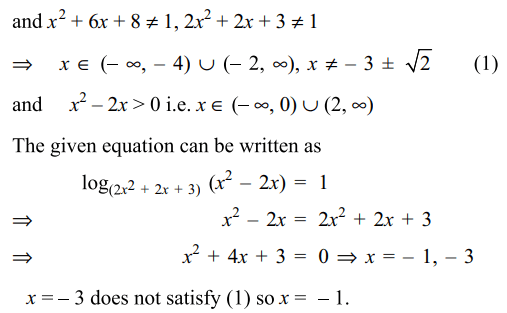
47. \[x^{\log_{5}x}>5\] implies
a) \[ x\epsilon \left(0, \infty\right)\]
b) \[ x\epsilon \left(0, 1/5\right) \cup \left(5,\infty\right)\]
c) \[ x\epsilon \left(1, \infty\right)\]
d) \[ x\epsilon \left(1, 2\right)\]
Explanation: Clearly x > 0, Taking logarithm with base 5,
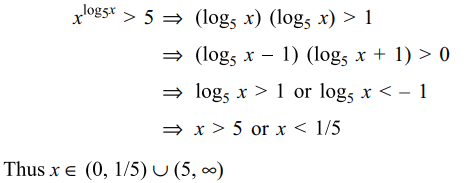
48. If \[\log x^{2} -\log 2x=3\log3-\log6\] then x equals
a) 9
b) 3
c) 4
d) 5
Explanation: Clearly x > 0
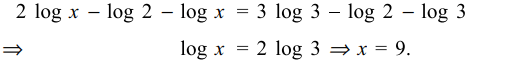
49. If \[\log_{0.5}\left(x-1\right)<\log_{0.25}\left(x-1\right)\] then x lies in the interval
a) \[\left(2,\infty\right)\]
b) \[\left(3,\infty\right)\]
c) \[\left(-\infty,0\right)\]
d) \[\left(0,3\right)\]
Explanation:
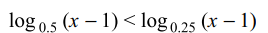
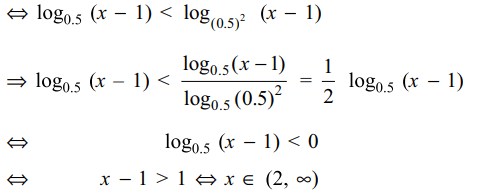
50. If \[N=n!\left(n \epsilon N,n>2\right)\] then \[\lim_{N \rightarrow\infty}\left[\left(\log_{2}N\right)^{-1}+\left(\log_{3}N\right)^{-1}+....+\left(\log_{n}N\right)^{-1}\right]\]
is
a) 2
b) 3
c) 4
d) 1
Explanation: