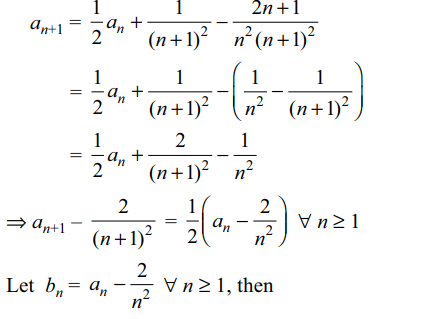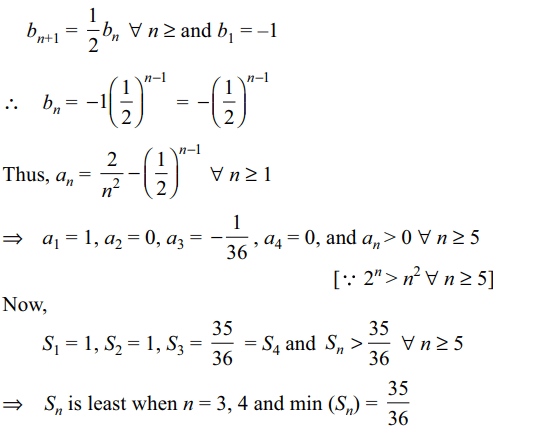1. Value of \[\lim_{n \rightarrow \infty}\sum_{r=1}^{n}\tan^{-1}\left(\frac{1}{2r^{2}}\right)\]
is
a) \[\pi/2\]
b) \[\pi/4\]
c) 1
d) \[\pi/8\]
Explanation:
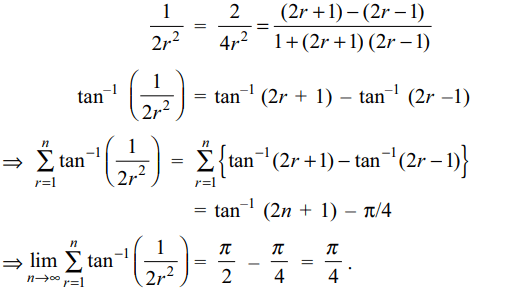
2. Let \[I_{n}=\int_{0}^{\pi/4} \tan^{n}x dx \] . then \[I_{2}+I_{4},I_{3}+I_{5},I_{4}+I_{6},I_{5}+I_{7},....\]
are in
a) A.P.
b) G.P.
c) H.P.
d) none of these
Explanation: We have for r ≥ 1,

3.If \[\sum_{r=1}^{n} t_{r}=\frac{1}{6}n \left(n+1\right) \left(n+2\right) \forall n\geq 1\]
then
\[\lim_{n \rightarrow \infty}\sum_{r=1}^{n} \frac{1}{t_{r}}\] is
a) 2
b) 3
c) 3/2
d) 6
Explanation: We have, for n ≥ 1,
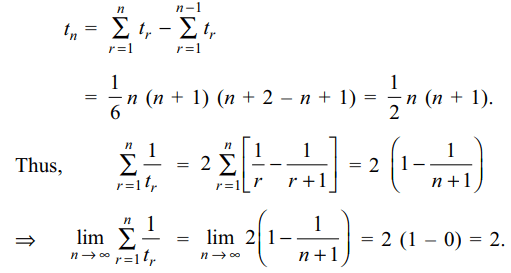
4. If \[H_{n}=1+\frac{1}{2}+...+\frac{1}{n}\] , then value of
\[S_{n}=1+\frac{3}{2}+\frac{5}{3}+...+\frac{2n-1}{n}\] is
a) \[H_{n}+n\]
b) \[2n-H_{n}\]
c) \[\left(n-1\right)+H_{n}\]
d) \[H_{n}+2n\]
Explanation:
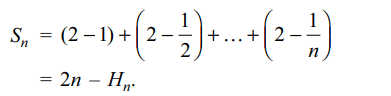
5. Sum to n terms of \[S_{n}=1+\frac{3}{2}+\frac{7}{4}+\frac{15}{8}+\frac{31}{16}+....\]
is
a) \[2\left(n-1\right)+\frac{1}{2^{n-1}}\]
b) \[2n-\frac{1}{2^{n}}\]
c) \[2+\frac{1}{2^{n}}\]
d) \[2n-1+\frac{1}{2^{n}}\]
Explanation:
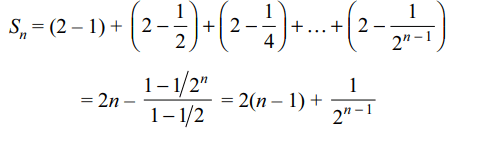
6. Let \[a_{k}=\frac{\sqrt{\left(k-1\right)k}}{\sqrt{2k-1+2\sqrt{k\left(k-1\right)}}}\]
\[k\epsilon N\] ,then
a) \[a_{k}<\frac{1}{2}\sqrt{k} \forall k\epsilon N\]
b) \[\sum_{k=1}^{n}a_{k}<\frac{1}{2}\int_{0}^{n} \sqrt{x} dx\]
c) \[\sum_{k=1}^{n}a_{k}<\frac{1}{3}n \sqrt{n}\]
d) All of the Above
Explanation:
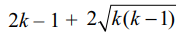
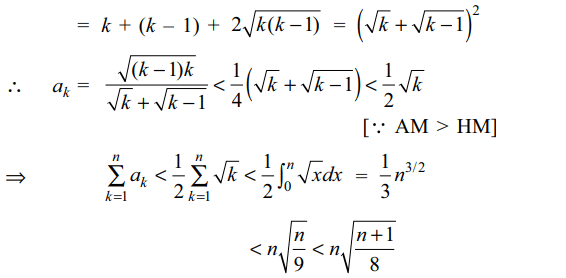
7. For 0 < x < 1, x > 1, let
\[a_{k}= \frac{kx^{k-1}}{1+x+...+x^{k-1}}\]
then \[\sum_{k=1}^{n}a_{k}\]
connot exceed
a) \[\frac{\left(\sqrt{x}\right)^{n}-1}{\sqrt{x}-1}\]
b) \[\frac{2\left(x^{n}-1\right)}{x-1}\]
c) \[2\left(1+x+..+x^{n-1}\right)\]
d) All of the Above
Explanation:
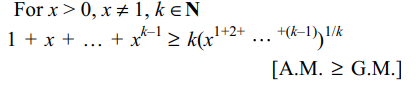
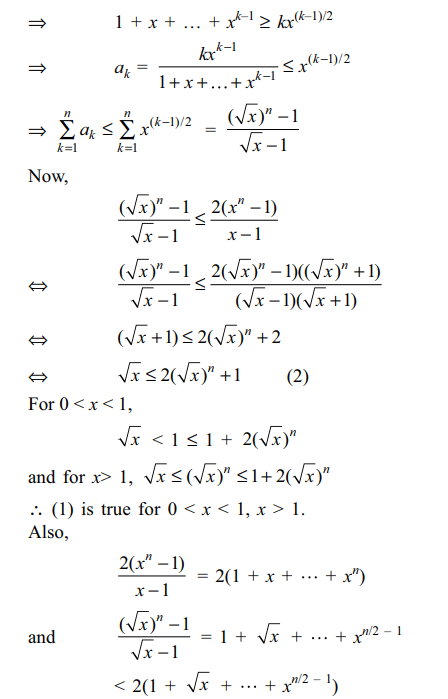
8. If a, b, c are in H.P., then
a) \[\frac{a}{b+c-a},\frac{b}{c+a-b},\frac{c}{a+b-c}\] are in H.P
b) \[\frac{2}{b}=\frac{1}{b-a}+\frac{1}{b-c}\]
c) \[a-\frac{b}{2},\frac{b}{2},c-\frac{b}{2}\] are in G.P
d) All of the Above
Explanation:
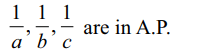
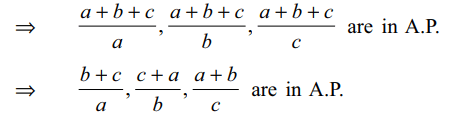
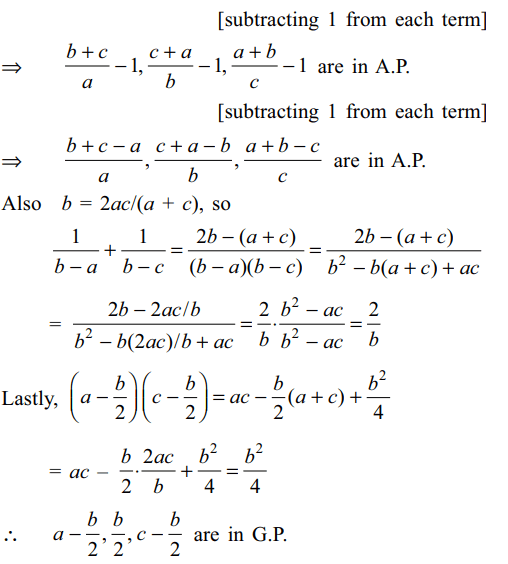
9. Let \[a_{n}=2n+5,b_{n}=\left(\frac{1}{3}\right)^{n}\forall n\epsilon N\] . If
\[\sum_{k=1}^{n}a_{k}b_{k}c_{k}=\frac{1}{3}\left(n+1\right)\left(n+2\right)\left(n+3\right)\] , then
a) \[c_{1}=24/7\]
b) \[c_{n}=\frac{\left(n+1\right)\left(n+2\right)3^{n}}{2n+5} \forall n \geq 2\]
c) \[\sum_{n=1}^{\infty}\frac{1}{c_{n}}=\frac{29}{72}\]
d) All of the Above
Explanation:
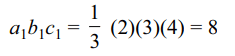
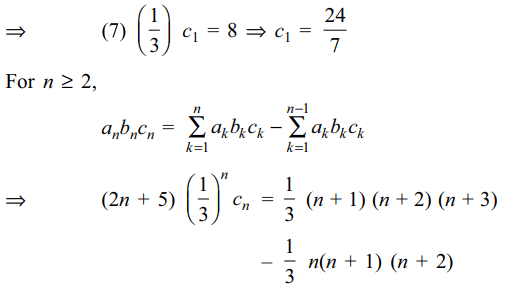
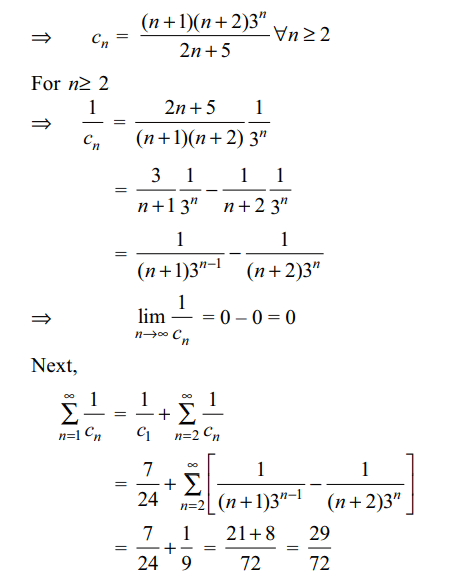
10.Let \[a_{1}=1 , a_{n+1}=\frac{1}{2}a_{n}+\frac{n^{2}-2n-1}{n^{2}\left(n+1\right)^{2}} \forall n\geq 1\]
and \[S_{n}=a_{1}+a_{2}+...+a_{n} \]
a) \[a_{n}=\frac{2}{n^{2}}-\left(\frac{1}{2}\right)^{n-1}\forall n\geq 1\]
b) \[S_{n}\] is minimum for n = 3
c) \[S_{n}\] is minimum for n = 4
d) All of the Above
Explanation: For n ≥ 1,