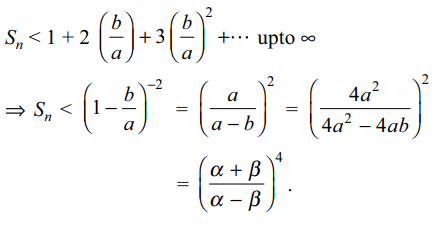1. If the first and (2n+1)th terms of an
A.P.; G.P. and H.P. of positive terms are equal and their
(n + 1)th terms are a, b and c respectively, then
a) \[a \geq b \geq c\]
b) \[ac=b^{2}\]
c) a, b, c are in G.P.
d) All of the Above
Explanation: Let A be the first term, D be the common difference and B be the (2n + 1)th term of the A.P., then
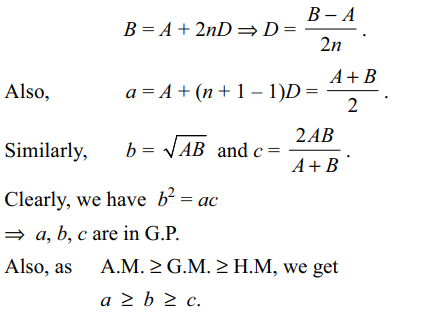
2. For a positive integer n, let
\[a\left(n\right)=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+....+\frac{1}{\left(2^{n}\right)-1}\]
Then
a) a(n) < n
b) \[a\left(n\right)>\frac{n}{2}\]
c) a(2n) > n
d) All of the Above
Explanation:
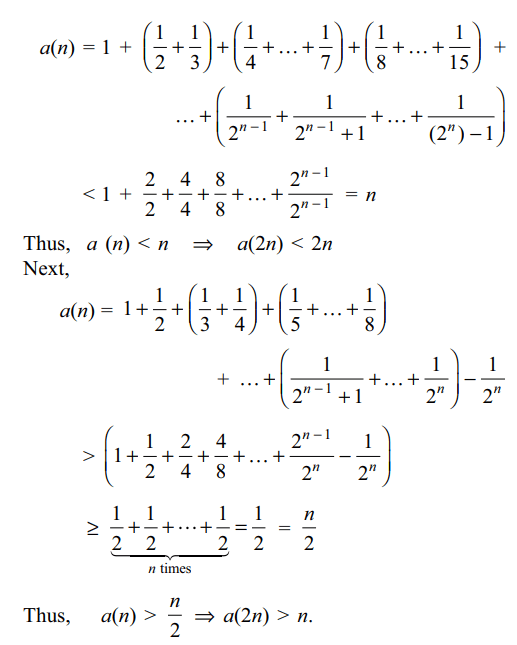
3. Given a sequence of four numbers such that the first three are in G.P. and the last three are in A.P. with common difference 6. If the
first and the fourth number are equal, then common ratio of the G.P. is
a) -2
b) 2
c) 3
d) -3
Explanation:
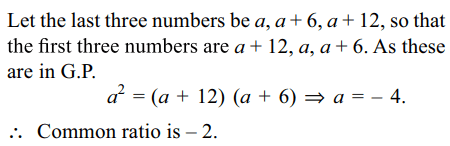
4.The sum of the series
\[\frac{7}{1^{3}.2^{3}}+\frac{19}{2^{3}.3^{3}}+\frac{37}{3^{3}.4^{3}}+.... \] ∞
is
a) 3
b) 2
c) 1
d) 1.5
Explanation:
5. \[\lim_{n \rightarrow \infty}[\frac{1^{2}+2^{2}+...+n^{2}}{5n^{3}}+\frac{4(1^{3}+2^{3}+...+n^{3})}{3n^{4}}+\frac{1+2+...+n}{n^{2}}]\]
equals
a) 9/10
b) 1/10
c) 1/2
d) 1/3
Explanation: 9/10
6. \[\lim_{n \rightarrow \infty}\left(\frac{1}{n^{100}}\sum_{r=1}^{n}r^{99}\right)\]
equals
a) \[\frac{1}{99}\]
b) \[\frac{1}{100}\]
c) \[\frac{1}{101}\]
d) 0
Explanation:
7. Let \[S_{k}\left(n\right)=\sum_{r=1}^{n}r^{k}\] , then \[\lim_{n \rightarrow \infty}\frac{S_{1}\left(n\right)S_{5}\left(n\right)-S_{3}\left(n\right)^2}{S_{7}\left(n\right)}\]
a) 1/3
b) -1/3
c) 1/6
d) -1/6
Explanation:
8. If x, y, z are real and
\[4x^{2}+9y^{2}+16z^{2}-6xy-12yz-8zx=0\]
then x, y, z are
a) A.P.
b) G.P.
c) H.P.
d) A.G.P.
Explanation:

9. If a, b, c are three distinct numbers such that a, b,
c are in A.P. and a, c – b, b – a are in G.P. then the
ratio a : b : c equals
a) 1 : 2 : 4
b) 1 : 3 : 5
c) 1 : 2 : 3
d) 1 : 3 : 8
Explanation:
10. Let \[\alpha,\beta\] be two positive roots of
\[x^{2}-2ax+ab=0\] where 0 < a < b, then for \[n\epsilon N\]
\[S_{n}=1+2\left(\frac{b}{a}\right)+3\left(\frac{b}{a}\right)^{2}+...+n\left(\frac{b}{a}\right)^{n}\]
cannot exceed
a) \[\frac{\alpha}{\beta}\]
b) \[|\frac{\alpha+\beta}{\alpha-\beta}|\]
c) \[\frac{\beta}{\alpha}\]
d) \[(\frac{\alpha+\beta}{\alpha-\beta})^{4}\]
Explanation: