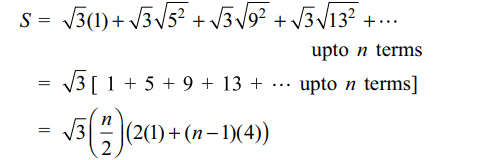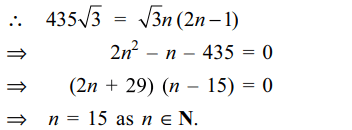PrepBharat

1. If \[1^{2}+2^{2}+3^{2}+...+2003^{2}=\left(2003\right)\left(4007\right)\left(334\right)\]
and \[\left(1\right)\left(2003\right)+\left(2\right)\left(2002\right)+\left(3\right)\left(2001\right)+...+\left(2003\right)\left(1\right)=\left(2003\right)\left(334\right)\left(x\right)\]
then x equals
a) 2005
b) 2004
c) 2003
d) 2001

View Answer

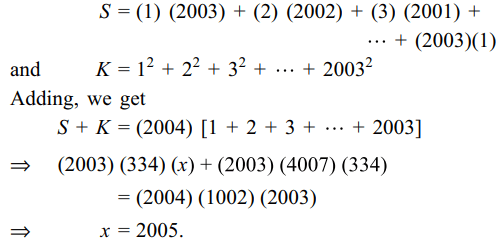
2. Sum of the series \[\frac{1}{2^{2}-1}+\frac{1}{4^{2}-1}+\frac{1}{6^{2}-1}+....\]       upto 2n terms is
a) \[\frac{n}{2n+1}\]
b) \[\frac{1}{2n+1}\]
c) \[\frac{1}{n+1}\]
d) \[\frac{4}{2n-1}\]

View Answer

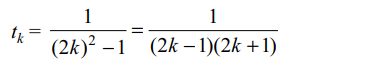
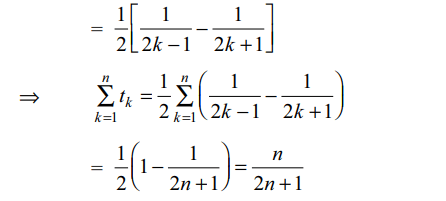
3. Let \[a_{1},a_{2},....,a_{10}\]   be in A.P. and \[h_{1},h_{2},....,h_{10}\]   be in H.P. If \[a_{1}=h_{1}=2\]   and \[a_{10}=h_{10}=3\]   , then a₅ h₆ is
a) 2
b) 3
c) 5
d) 6

View Answer

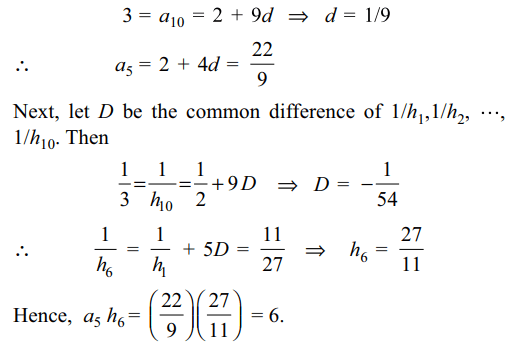
4. Suppose a, b, c are in A.P. and \[a^{2},b^{2},c^{2}\]   are in G.P. If a < b < c and a + b + c = 3/2, then the value of a is
a) \[\frac{1}{2\sqrt{2}}\]
b) \[\frac{1}{2\sqrt{3}}\]
c) \[\frac{1}{2}-\frac{1}{\sqrt{3}}\]
d) \[\frac{1}{2}-\frac{1}{\sqrt{2}}\]

View Answer

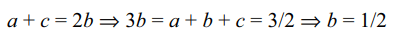
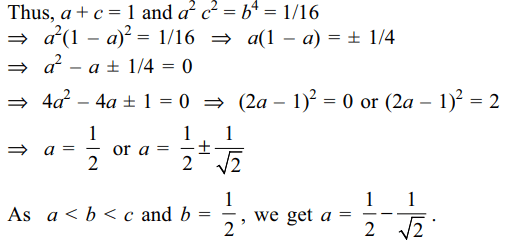
5. Let \[S_{1},S_{2},....\]   be squares such that for each n ≥ 1, the length of a side of \[S_{n}\] equals the length of a diagonal of \[S_{n+1}\] . If the length of a side of \[S_{1}\] is 10 cm, then the smallest value of n for which Area \[\left(S_{n}\right)< 1\]   is
a) 7
b) 8
c) 9
d) 10

View Answer

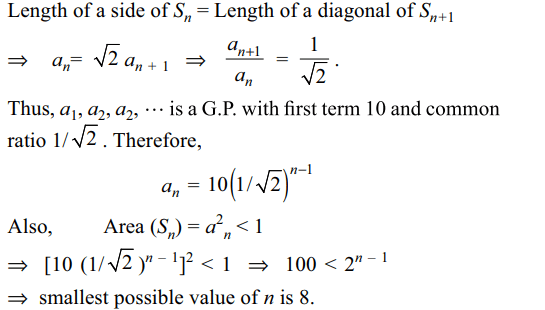
6. If a, b, c are in G.P., and log a – log 2b, log 2b – log 3c and log 3c – log a are in A.P., then a, b, c are the lengths of the sides of a triangle which is
a) acute-angled
b) obtuse-angled
c) right-angled
d) equilateral.

View Answer

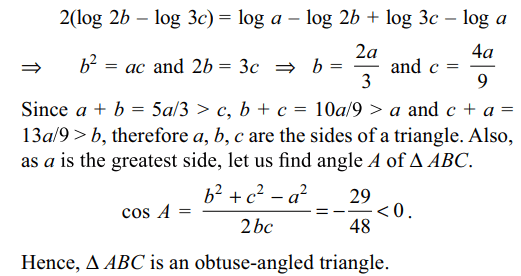
7. If \[x_{1},x_{2}...x_{n}\]   are n non-zero real numbers such that \[\left(x_2^1+x_2^2+...+x_{n-1}^{2}\right)\left(x_2^2+x_3^2+...+x_{n}^{2}\right)\leq \left(x_{1}x_{2}+x_{2}x_{3}+...+x_{n-1}x_{n}\right)^{2}\]
then \[x_{1},x_{2},...,x_{n}\]   are in
a) A.P
b) G.P
c) H.P
d) A.G.P

View Answer

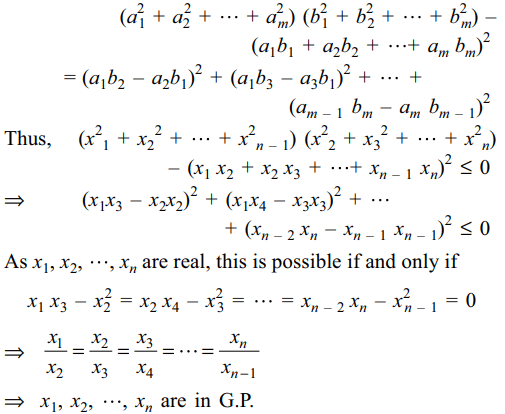
8. If three positive real numbers a, b, c (c > a) are in H.P., then log (a + c) + log (a – 2b + c) is equal to
a) 2 log (c – b)
b) 2 log (a + c)
c) 2 log (c – a)
d) log a + log b + log c.

View Answer

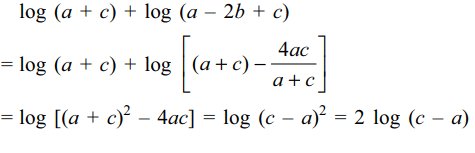
9. If \[a_{1},a_{2},...,a_{n}\]   are in A.P. with common difference \[d\neq 0\] , then the sum of the series
sin d [cosec a₁ cosec a₂ + cosec a₂ cosec a₃+....+cosec a_n-1cosec a_n] is
a) \[\sec a_{1}-\sec a_{n}\]
b) cosec a₁ - cosec a_n
c) \[\cot a_{1}-\cot a_{n}\]
d) \[\tan a_{1}-\tan a_{n}\]

View Answer

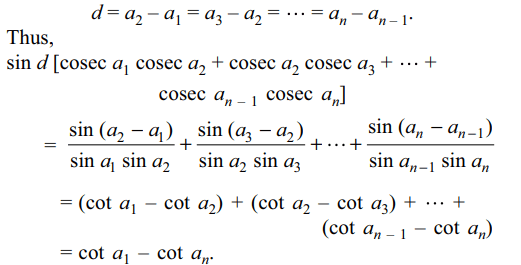
10. If sum of first n terms of the series \[S=\sqrt{3}+\sqrt{75}+\sqrt{243}+\sqrt{507}+....\]       is \[435\sqrt{3}\] , then n is equal to
a) 14
b) 15
c) 19
d) 21

View Answer