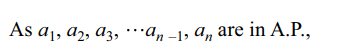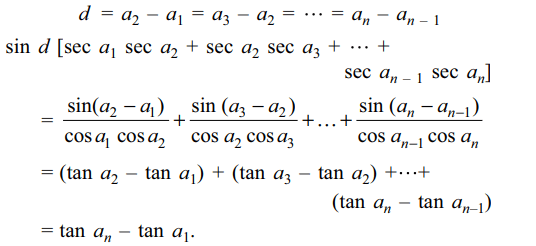1. If the ratio of sums to n terms of two A.P’s
is (5n + 3) :(3n+4) then the ratio of their 17th terms is
a) 172 : 99
b) 168 : 103
c) 175 : 99
d) 171 : 103
Explanation: Let two A.P.’s be
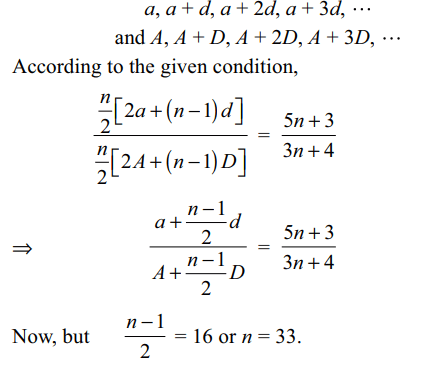
2. If \[H_{1},H_{2},....,H_{n}\] are n harmonic means
between a and \[b\left(\neq a\right)\] , then value of \[\frac{H_{1}+a}{H_{1}-a}+\frac{H_{n}+b}{H_{n}-b}\] is
equal to
a) n + 1
b) n - 1
c) 2n
d) 2n + 3
Explanation: As a, H1, H2, .... , Hn, b are in H.P
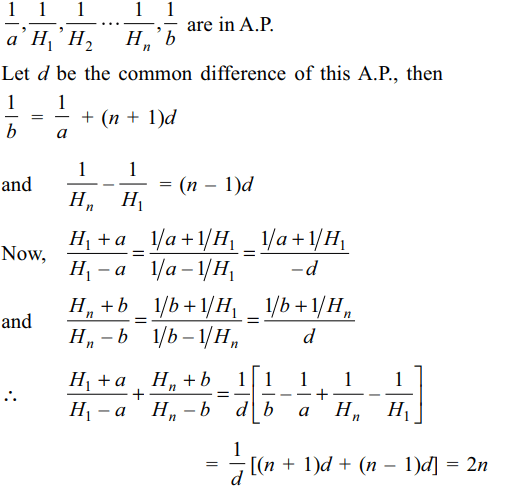
3. Let \[a_{1},a_{2},....,a_{n}\] be n positive real numbers
such that \[a_{1}a_{2}....a_{n}=c\] , where c number. The
expression \[a_{1}+2a_{2}+3a_{3}+....+na_{n}\] cannot be less than
a) n! c
b) \[n\left(n! c\right)^{1/n}\]
c) \[C^{1/n}\]
d) \[\left(2n\right)C^{1/n}\]
Explanation:
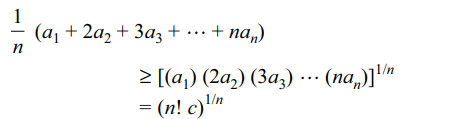
4. The sum upto (2n + 1) terms of the series
\[a^{2}-\left(a+d\right)^{2}+\left(a+2d\right)^{2}-\left(a+3d\right)^{2}+....\]
is
a) \[a^{2}+3nd ^{2}\]
b) \[a^{2}+2nad +n\left(n-1\right)d^{2}\]
c) \[a^{2}+3nad +n\left(n-1\right)d^{2}\]
d) \[a^{2}+2nad +n\left(2n+1\right)d^{2}\]
Explanation: We can write the sum upto (2n + 1) terms as
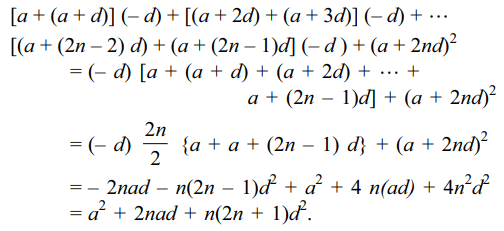
5. Value of
y=\[(0.64)^{\log_{0.25}\left(\frac{1}{3}+\frac{1}{3^{2}}+\frac{1}{3^{3}}+.... \infty\right)} \]
is
a) 0.9
b) 0.8
c) 0.6
d) 0.25
Explanation:
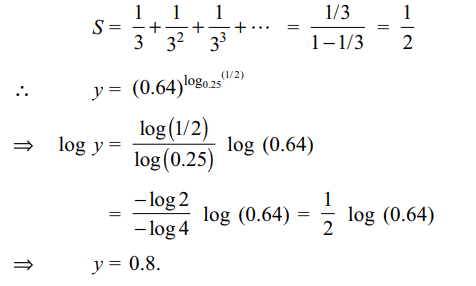
6. Let \[ax^{2}+\frac{b}{x}\geq c\] for all positive x, where
a > 0 and b>0. The value of the expression \[27 ab^{2}\] cannot
be less than
a) \[4c^{3}\]
b) \[4c^{2}\]
c) \[8c^{3}\]
d) \[c^{3}\]
Explanation: As A.M. ≥ G.M., we get
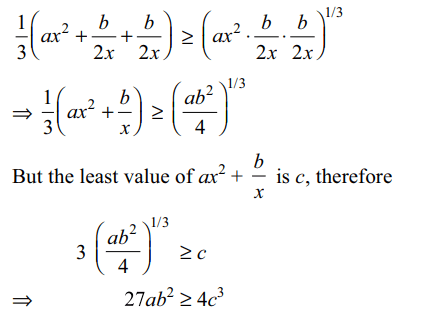
7.Let \[b_{i}>1\] for i = 1, 2, …, 101. Suppose
\[\log_{e}b_{1},\log_{e}b_{2},.....,\log_{e}b_{101}\] are in Arithmetic Progression
(A.P.) with the common difference \[log_{e} 2\] . Suppose \[a_{1},a_{2},....,a_{101}\]
are in A.P. such that \[a_{1}=b_{1}\] and \[a_{51}=b_{51}\] . If \[t= b_{1}+b_{2}+....+b_{51}\]
and \[S= a_{1}+a_{2}+....+a_{51}\] , then
a) \[S> t\] and \[a_{101}>b_{101}\]
b) \[S> t\] and \[a_{101}< b_{101}\]
c) \[S< t\] and \[a_{101}>b_{101}\]
d) \[S< t\] and \[a_{101}< b_{101}\]
Explanation: logeb1, logeb2, .…, logeb101 are in A.P. with
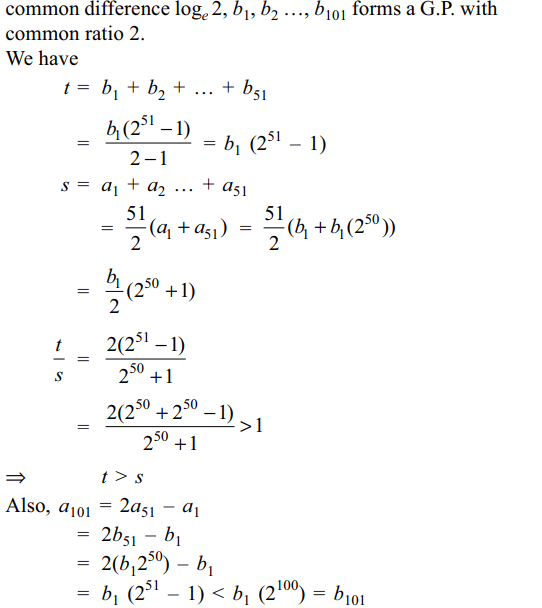
8.If \[S_{n}=\sum_{r=1}^{n}t_{r}=\frac{1}{6}n\left(2n^{2}+9n+13\right)\] , then
\[\sum_{r=1}^{n}\sqrt{t_{r}}\]
equals
a) \[\frac{1}{2}n\left(n+1\right)\]
b) \[\frac{1}{2}n\left(n+2\right)\]
c) \[\frac{1}{2}n\left(n+3\right)\]
d) \[\frac{1}{2}n\left(n+5\right)\]
Explanation:
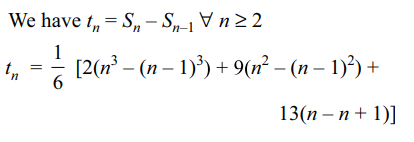
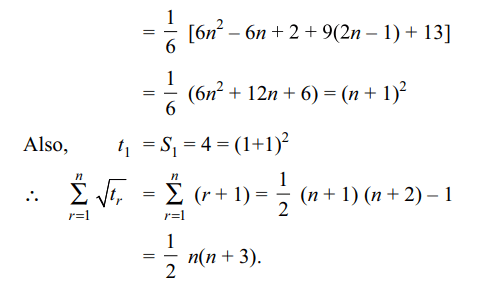
9. If 0< \[\theta\] , \[\phi < \pi/2\] and \[x=\sum_{n=0}^{\infty} \sin^{2n}\theta,y=\sum_{n=0}^{\infty} \cos^{2n}\phi,\]
and \[z=\sum_{n=0}^{\infty} \cos^{n}\left(\theta+\phi\right)\cos^{n}\left(\theta-\phi\right)\]
a) xyz + 1 = yz – zx
b) xyz – 1 = yz + zx
c) xyz – xy = yz – zx
d) xyz + 1 = yz + zx
Explanation:
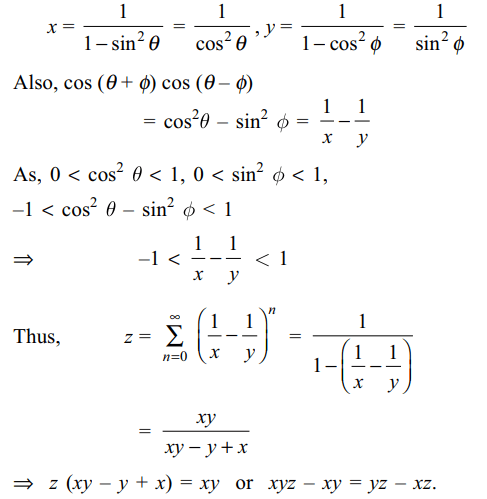
10. If \[a_{1},a_{2},....,a_{n}\] are in A.P. with common
difference d \[\neq\] 0, then sum of the series \[\sin d\left[\sec a_{1}\sec a_{2}+\sec a_{2}\sec a_{3}+....+\sec a_{n-1}\sec a_{n}\right]\]
is
a) \[\tan a_{n}-\tan a_{1}\]
b) \[\cot a_{n}-\cot a_{1}\]
c) \[\sec a_{n}-\sec a_{1}\]
d) cosec an - cosec a1
Explanation: