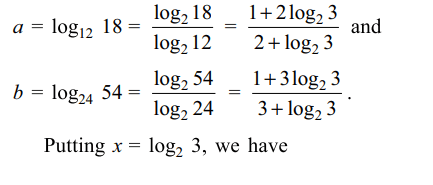1. Solutons set of the inequality \[\log_{x}\left(2x^{2}+x-1\right)>\log_{x}\left(2\right)-1\]
is
a) \[\left(1/2 ,1\right)\]
b) \[\left(1/2 ,1\right)\cup\left(1,\infty\right)\]
c) \[\left(1,\infty\right)\]
d) \[\left(0,1\right)\]
Explanation: It holds for 1/2 < x < 1, x > 1
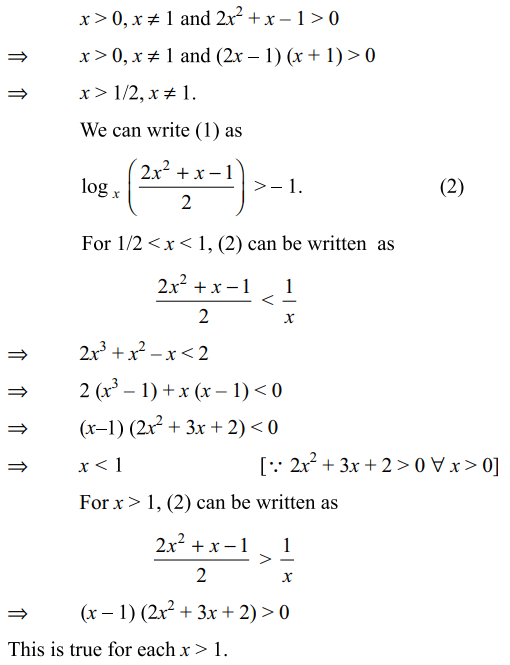
2. The value of of x stisfying \[\log_{2}\left(3x-2\right)=\log_{1/2}x\]
is
a) -1/3
b) 2
c) 1/2
d) 1
Explanation:
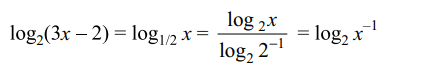

3. The solutions of the equations \[4^{\log_{2}\log x}=\log x-\left(\log x\right)^{2}+1\]
is
a) x = 1
b) x = 4
c) x = e
d) \[x = e^{2}\]
Explanation:
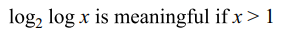
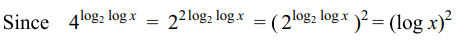
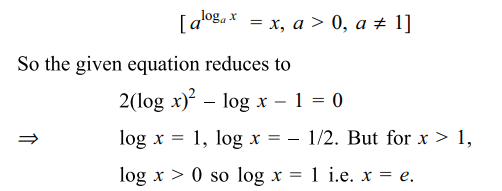
4. The set of all x satisfying the equations \[x^{\log_{3}x^{2}+\left(\log_{3} x\right)^{2}-10} =1/x^{2}\]
is
a) \[\left\{ 1,9\right\}\]
b) \[\left\{ 1,9,1/81\right\}\]
c) \[\left\{ 1,4, 1/81\right\}\]
d) \[\left\{ 9,1/81 \right\}\]
Explanation: Taking log of both the sides with base 3, we have
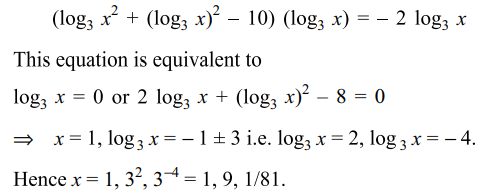
5.The set of all solutions of the inequality \[\left(1/2\right)^{x^{2}-2x}< 1/4\] contains the sets
a) \[\left(-\infty ,0\right)\]
b) \[\left(-\infty ,1\right)\]
c) \[\left(1,\infty \right)\]
d) \[\left(3,\infty \right)\]
Explanation:

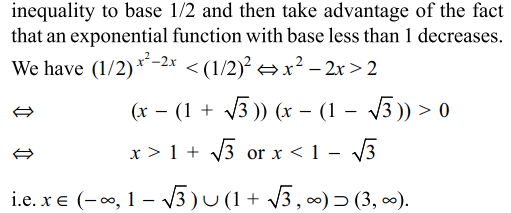
6. The set of all the solutions of the inequality \[\log_{1-x}\left(x-2\right)\geq -1\] is
a) \[\left(-\infty ,0\right)\]
b) \[\left(2,\infty \right)\]
c) \[\left(-\infty ,1\right)\]
d) \[\phi\]
Explanation:
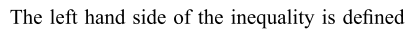

7. If \[\log_{3}x+\log_{3}y = 2+\log_{3}2\] and \[\log_{3}\left(x+y\right)=2\] then
a) x = 1, y = 8
b) x = 8, y = 1
c) x = 3, y = 6
d) x = 9, y = 3
Explanation:
8. The set of all solutions of the equations \[\log_{3}x\log_{4}x\log_{5}x=\log_{3}x\log_{4}x+\log_{4}x\log_{5}x+\log_{5}x\log_{3}x\]
is
a) {1}
b) {1,60}
c) {1,5,10,60}
d) {1,4,8,60}
Explanation:
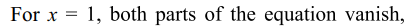
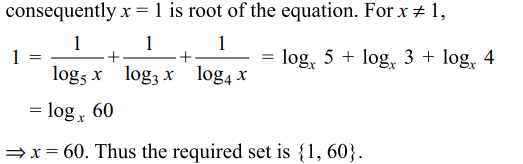
9. If \[\log_{30}3=c,\log_{30}5=d\] then the value of \[\log_{30}8\]
a) 2(1-c-d)
b) 3(1+c+d)
c) 3(1+c-d)
d) 3(1-c-d)
Explanation:
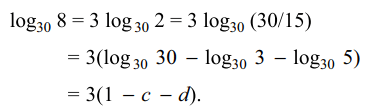
10. if \[a=\log_{12}18,b=\log_{24}54\] then the value of ab+5(a-b) is
a) 0
b) 4
c) 1
d) 8
Explanation: