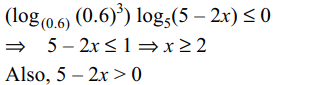1. If x satisfies \[\log_{3}\left(2x+1\right)<\log_{3}5\] then x contains the intervals (s)
a) \[\left(-\frac{1}{2},0\right)\]
b) \[\left[0,2\right)\]
c) \[\left[1,2\right)\]
d) All of the Above
Explanation:
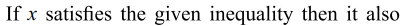
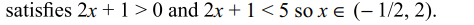
2. If \[x\epsilon R\] satisfies \[\left(\log_{10}\left(100\right)x\right)^{2}+\left(\log_{10}10x\right)^{2}+\log_{10}x \leq 14\]
then x contains the interval.
a) \[\left(1,10\right]\]
b) \[\left[10^{-9/2},1\right)\]
c) \[\left(0,\infty\right)\]
d) Both a and b
Explanation:
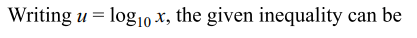
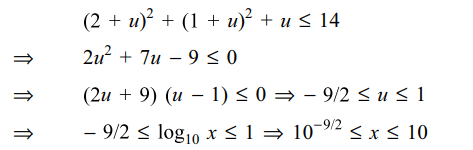
3. For x, y, z>1, let
\[\alpha=\frac{ln\left(xy\right)}{ln\left(xye\right)}+\frac{ln\left(yz\right)}{ln\left(yze\right)}+\frac{ln\left(zx\right)}{ln\left(zxe\right)}\]
and \[\beta=\frac{ln\left(x\right)}{ln\left(xe\right)}+\frac{ln\left(y\right)}{ln\left(ye\right)}+\frac{ln\left(z\right)}{ln\left(ze\right)}\]
a) \[\alpha >\beta\]
b) \[\alpha < 2\beta\]
c) \[\alpha =\beta\]
d) Both a and b
Explanation:
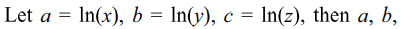
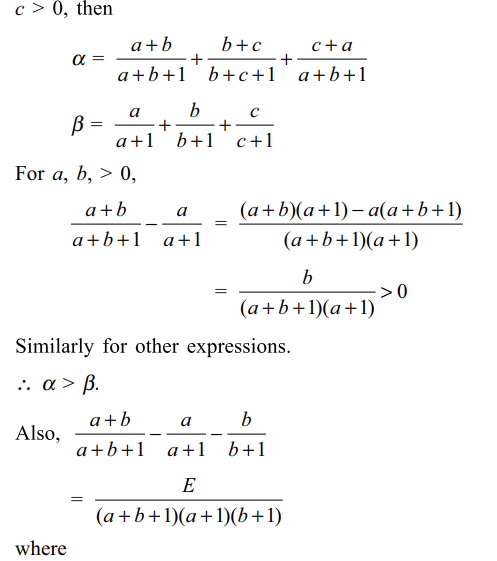
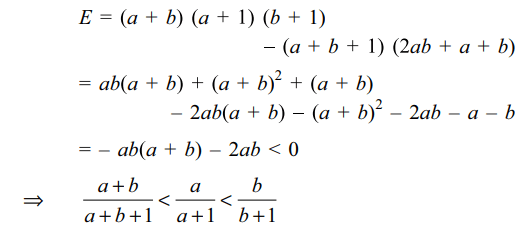
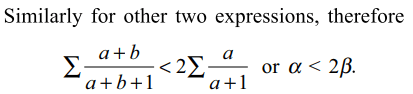
4. Let S be solution set of \[\left(\frac{1}{2}\right)^{x+1}=3^x\] and T be solution set of \[\left(\frac{1}{3}\right)^{x+1}=2^x\] then
a) S contains exactly one element
b) T contains exactly one element
c) \[S\cap T=\phi\]
d) All of the Above
Explanation:
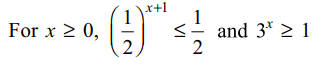
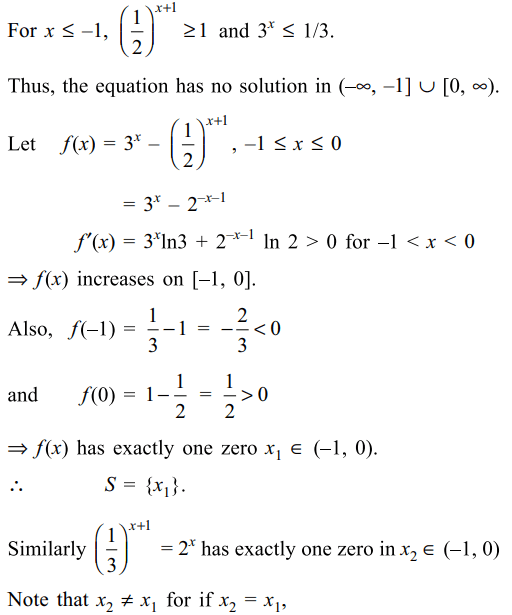
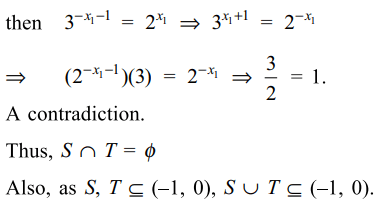
5. Let \[\log x=\log_{10}x\] and suppose x,y,z>1 , then least value of the expression
\[E=\log \left(xyz\right)\sum\left(\frac{\log x}{\log y\log z}+\frac{\log y}{\log x\log z}\right)\]
a) 9
b) 18
c) 27
d) 36
Explanation:
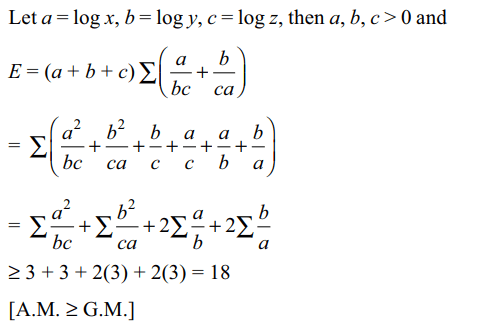
6. Number of real value of x for which \[2017^{x}+2018^{x}+2019^{x}=3018^{x}\]
is
a) 0
b) 1
c) 2
d) infinite
Explanation:
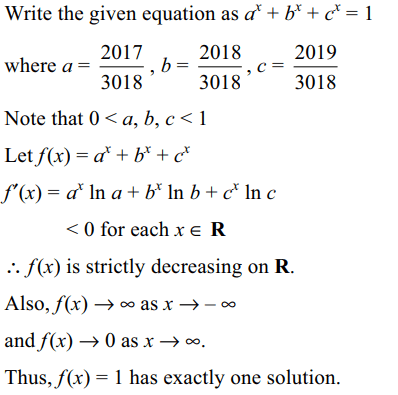
7. Number of solutions of \[e^{x} = x^{e}\] is
a) 0
b) 1
c) 2
d) infinite
Explanation:
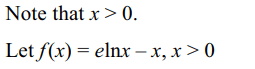
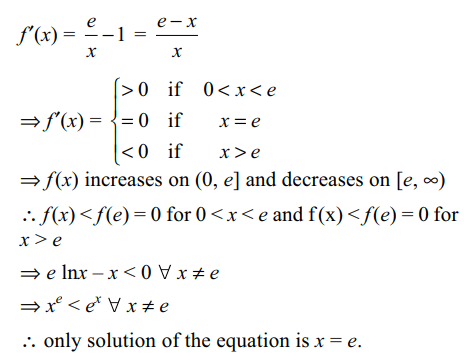
8. If 0< x,y< 1 and \[\log_{x}\left(a\right)+\log_{y}\left(a\right)=4\log_{xy}\left(a\right)\] for some
a>0, \[a\neq1\] then
a) x + y = 2
b) x + y = 1
c) x=y
d) \[xy=a^{2}\]
Explanation:
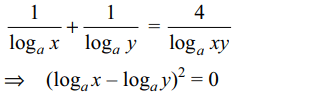
9. The value of x satisfying
\[\log_{3}\left(5x-2\right)-2\log_{3}\sqrt{3x+1}=1-\log_{3}4\]
is
a) 2
b) 1
c) 3
d) 4
Explanation: 1
10. If \[S=\left\{x\epsilon R:\left(\log_{0.6}0.216\right)\log_{5}\left(5-2x\right)\leq 0\right\}\]
then S is equal to
a) \[\left[2.5,\infty\right)\]
b) \[\left[2,2.5\right)\]
c) \[\left(2,2.5\right)\]
d) \[\left[0,2.5\right)\]
Explanation: