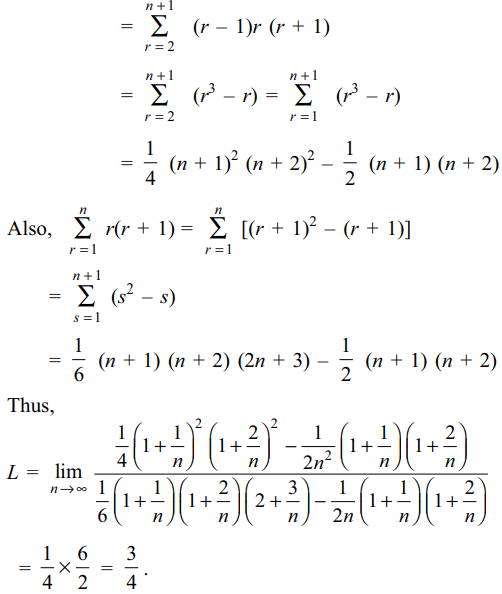PrepBharat

1. Sum to n terms of the series \[\frac{1}{1.2.3.4}+\frac{1}{2.3.4.5}+\frac{1}{3.4.5.6}+....\]
is
a) \[\frac{n^{3}}{3\left(n+1\right)\left(n+2\right)\left(n+3\right)}\]
b) \[\frac{n^{3}+6n^{2}-3n}{6\left(n+2\right)\left(n+3\right)\left(n+4\right)}\]
c) \[\frac{15n^{2}+7n}{4n\left(n+1\right)\left(n+5\right)}\]
d) \[\frac{n^{3}+6n^{2}+11n}{18\left(n+1\right)\left(n+2\right)\left(n+3\right)}\]

View Answer

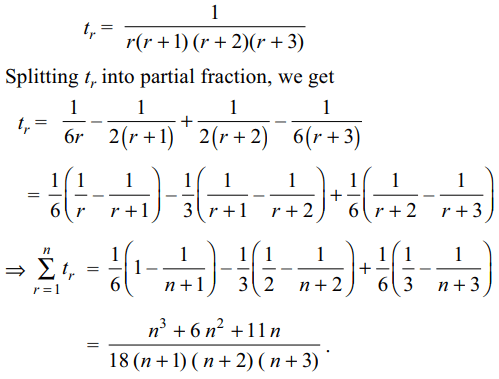
2. Sum of all the products of the first n positive integers taken two at a time is
a) \[\frac{1}{24}\left(n-1\right)n\left(n+1\right)\left(3n+2\right)\]
b) \[\frac{1}{48}\left(n-2\right)\left(n-1\right)n^{2}\]
c) \[\frac{1}{6}n\left(n+1\right)\left(n+2\right)\left(n+5\right)\]
d) \[\frac{1}{3}n\left(n+1\right)\left(n+2\right)\]

View Answer

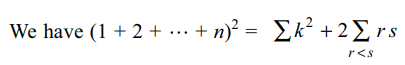
3. For a positive integer n, let \[a\left(n\right)=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+....+\frac{1}{\left(2^{n}\right)-1}\]
a) a(100) < 100
b) a(100) > 100
c) a(200) < 100
d) a(2000) > 1000

View Answer

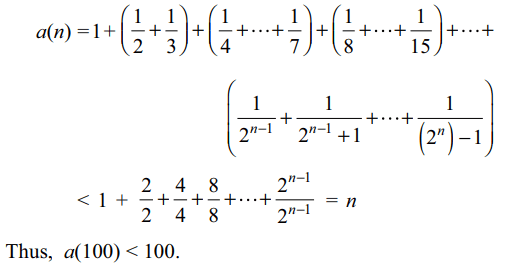
4. \[S_{n}\] , the sum to n terms of the series \[\left(n^{2}-1^{2}\right)+2\left(n^{2}-2^{2}\right)+3\left(n^{2}-3^{2}\right)+....\]
is
a) \[\frac{1}{4}n^{2}\left(n^{2}-1\right)\]
b) \[\frac{1}{4}n\left(n+1\right)^{2}\]
c) 0
d) \[2n\left(n^{2}-1\right)\]

View Answer

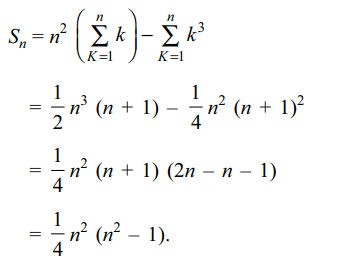
5. Let x be the arithmetic mean and y, z be the two geometric means between any two positive numbers. Then value of \[\frac{y^{3}+z^{3}}{xyz}\]   is
a) 2
b) 3
c) 1/2
d) 3/2

View Answer

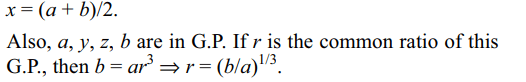
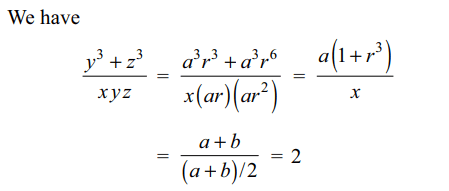
6. Let \[H_{n}=1+\frac{1}{2}+....+\frac{1}{n}\]    , then the sum to n terms of the series \[\frac{1^{2}}{1^{3}}+\frac{1^{2}+2^{2}}{1^{3}+2^{3}}+\frac{1^{2}+2^{2}+3^{2}}{1^{3}+2^{3}+3^{3}}+....\]
is
a) \[\frac{4}{3}H_{n}-1\]
b) \[\frac{4}{3}H_{n}+\frac{1}{n}\]
c) \[\frac{4}{3}H_{n}\]
d) \[\frac{4}{3}H_{n}-\frac{2}{3}\frac{n}{n+1}\]

View Answer

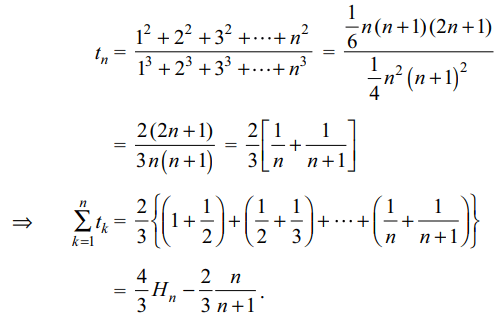
7. If the sum of first n terms of an A.P. is \[cn^{2}\], then sum of squares of these n terms is
a) \[\frac{1}{6}n\left(4n^{2}-1\right)c^{2}\]
b) \[\frac{1}{3}n\left(4n^{2}+1\right)c^{2}\]
c) \[\frac{1}{3}n\left(4n^{2}-1\right)c^{2}\]
d) \[\frac{1}{6}n\left(4n^{2}+1\right)c^{2}\]

View Answer

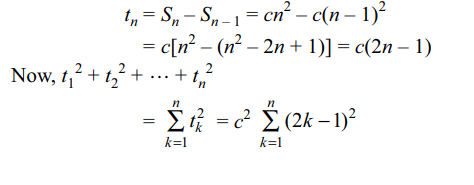
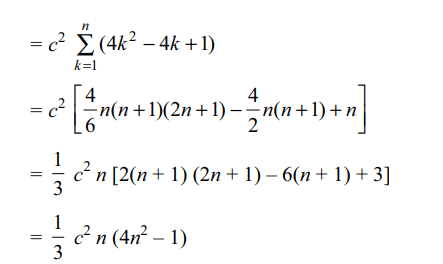
8. The sum of first n terms of the series \[1^{2}+2\times 2^{2}+3^{2}+2 \times4^{2}+5^{2}+2\times 6^{2}+....\]
is \[n\left(n+1\right)^{2}/2\]    when n is even. When n is odd the sum of the series is
a) \[n^{2}\left(3n+1\right)/4\]
b) \[n^{2}\left(n+1\right)/2\]
c) \[n^{3}\left(n-1 \right)/2\]
d) \[n\left(n+2\right)/2\]

View Answer

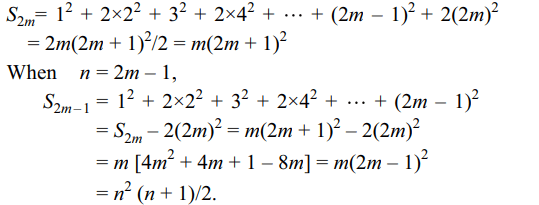
9. The interior angles of a polygon are in A.P. If the smallest angle is 120° and the common difference is 5°, then number of sides in the polygon is.
a) 7
b) 8
c) 9
d) 16

View Answer

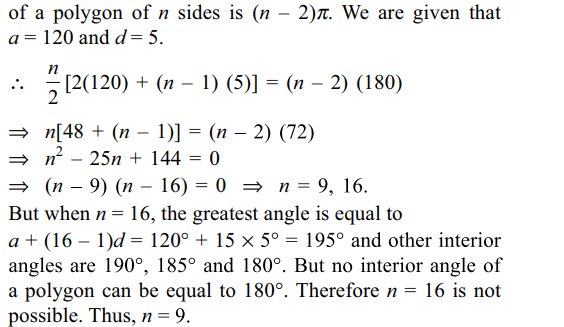
10. Let \[A_{n}=\frac{1.2.3+2.3.4+3.4.5+.... + n }{n\left(1.2+2.3+3.4+...+ n \right)}\]
then \[\lim_{n \rightarrow \infty} A_{n}\]   is
a) \[\frac{3}{4}\]
b) \[\frac{1}{4}\]
c) \[\frac{1}{2}\]
d) \[\frac{5}{4}\]

View Answer