PrepBharat

1. \[A=\begin{bmatrix}1 & 2 & 3 \\1 & 2 & 3 \\-1 & -2 & -3\end{bmatrix}\]     then A is a nilpotent matrix of index
a) 2
b) 3
c) 4
d) 5

View Answer

2. If \[A=\begin{bmatrix}\frac{1}{2}\left(e^{ix}+e^{-ix}\right) & \frac{1}{2}\left(e^{ix}-e^{-ix}\right) \\\frac{1}{2}\left(e^{ix}-e^{-ix}\right) & \frac{1}{2}\left(e^{ix}+e^{-ix}\right) \end{bmatrix}\]       then \[A^{-1}\] exists
a) for all real x
b) for positive real x only
c) for negative real x only
d) none of these

View Answer

3. If \[A=\begin{bmatrix}ab & b^{2} \\-a^{2} & -ab \end{bmatrix}\]     then \[A^{2}\] is equal
a) O
b) I
c) -I
d) None of the above

View Answer

4.If A is \[2 \times2\]  matrix such that \[A^{2}=O\]  , then tr (A) is
a) 1
b) -1
c) 0
d) none of these

View Answer

5. If \[A=\begin{bmatrix}a & b \\c & d \end{bmatrix}\]     such that A satisfies the relation \[A^{2}-\left(a+d\right)A=O\]     , then inverse of A is
a) I
b) A
c) (a+d) A
d) does not exist

View Answer

6. If \[A=\begin{bmatrix}3 & 2 \\0 & 1 \end{bmatrix}\]     , then \[A^{-3}\] is
a) \[\frac{1}{27}\begin{bmatrix}1 & -26 \\0 & -27 \end{bmatrix}\]
b) \[\frac{1}{27}\begin{bmatrix}-1 & -26 \\0 & -27 \end{bmatrix}\]
c) \[\frac{1}{27}\begin{bmatrix}1 & -26 \\0 & 27 \end{bmatrix}\]
d) \[\frac{1}{27}\begin{bmatrix}-1 & 26 \\0 & -27 \end{bmatrix}\]

View Answer

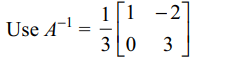
7. If A is a skew Hermitian matrix, then the main diagonal elements of A are all
a) zero
b) positive
c) negative
d) none of these

View Answer

8. If \[A=\begin{bmatrix}1 & 2 & 1 \\0 & 1 & -1 \\3 & -1 & 1\end{bmatrix}\]     then \[A^{3}-3A^{2}-A-9I\]     is equal to
a) O
b) I
c) A
d) \[A^{2}\]

View Answer

9.If \[A=\begin{bmatrix}\omega & -\omega \\-\omega & \omega \end{bmatrix}\]     and \[B=\begin{bmatrix}1 & -1 \\-1 & 1 \end{bmatrix}\]     ,then \[A^{9}\] equals
a) 64 B
b) 32 B
c) 16 B
d) 256 B

View Answer

10. If \[A=\begin{bmatrix}2 & 3-i & -i \\3+i & -5 & 7+i \\i & 7-i & e\end{bmatrix}\]      then A is
a) symmetric
b) Hermitian
c) skew Hermitian
d) none of these

View Answer