1. if \[f\left(x\right)=\begin{bmatrix}\sec^{2}x & 1 & 1 \\\cos^{2} x & \cos^{2} x & cosec^{2} x \\1 & \cos^{2} x & \cot^{2} x\end{bmatrix}\]
then
a) \[\int_{-\pi/4}^{\pi/4} f\left(x\right)dx=\frac{1}{32}\left(3\pi+8\right)\]
b) \[f'\left(\pi/2\right)=0\]
c) minimun value of \[f\left(x\right)\] is 1
d) All of the above
Explanation:
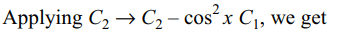
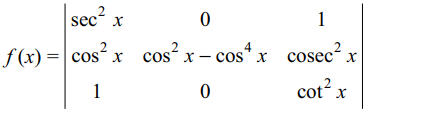
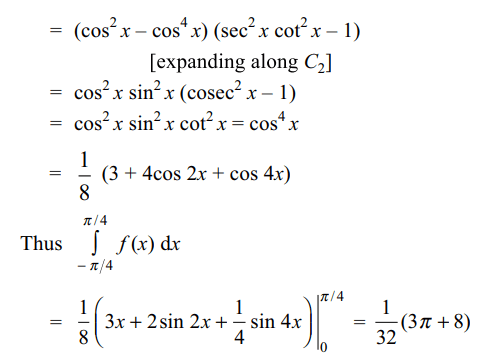
2. Let \[\triangle\left(x\right)=\begin{bmatrix}3 & 3x & 3x^{2}+2a^{2} \\3x & 3x^{2}+2a^{2} & 3x^{3}+6a^{2} x \\3x^{2}+2a^{2} & 3x^{3}+6a^{2} x & 3x^{4}+12a^{2}x^{2}+2a^{4} \end{bmatrix}\]
then
a) \[\triangle\]'(x) = 0
b) \[\triangle\](x) is independent of x
c) \[\int_{0}^{1} \triangle \left(x\right)dx=4a^{6}\]
d) All of the above
Explanation:
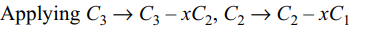
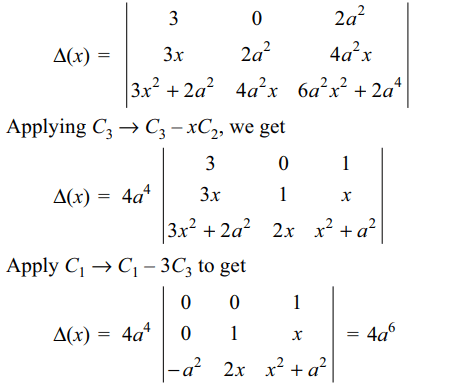
3. Let \[\lambda\] and \[\alpha\] be real. Let S denote the set
of all values of \[\lambda\] for which the system of linear equations
\[\lambda x+\left(\sin \alpha\right)y+\left(\cos \alpha\right)z=0\]
\[ x+\left(\cos \alpha\right)y+\left(\sin \alpha\right)z=0\]
\[ -x+\left(\sin \alpha\right)y-\left(\cos \alpha\right)z=0\]
has a non-trivial solution then S contains
a) (– 1, 1)
b) \[\left[-\sqrt{2},-1\right]\]
c) \[\left[1,\sqrt{2}\right]\]
d) All of the above
Explanation: The given system of linear equations will have a non-trivial solution if
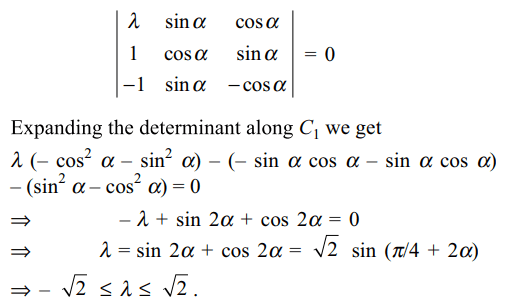
4. Consider the system of linear equations
in x, y and z:
(sin 3 \[\theta\] ) x – y + z = 0
(cos 2 \[\theta\] ) x + 4y + 3z = 0
2x + 7y + 7z = 0
The values of \[\theta\] for which the system of equations has a
non-trivial solution are
a) \[\left\{{n\pi : n\epsilon I}\right\}\]
b) \[\left\{{m\pi +\left(-1\right)^{m}\pi/6 : m\epsilon I}\right\}\]
c) \[\left\{{n\pi +\left(-1\right)^{n}\pi/3 : n\epsilon I}\right\}\]
d) Both a and b
Explanation: The given system of equations will have a non-trivial solution if
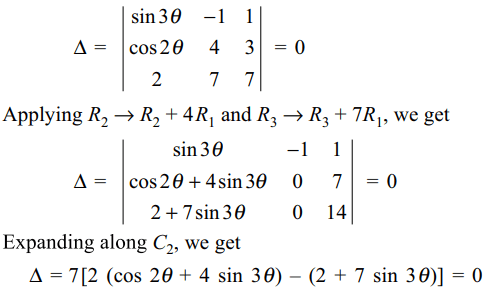
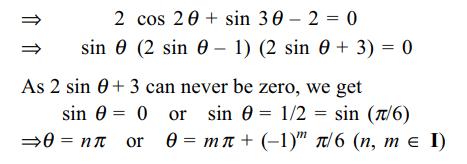
5. Let a, b, c, d be four real numbers and let
\[\triangle=\begin{bmatrix}2 & a+b+c+d & ac+cd \\a+b+c+d & 2\left(a+b\right)\left(c+d\right) & ab\left(c+d\right)+cd\left(a+b\right) \\ab+cd & ab\left(c+d\right)+cd\left(a+b\right) & 2abcd\end{bmatrix}\]
then \[\triangle\] is equal to
a) 2abcd (a + b) (c + d)
b) 2abcd (a + b + c + d)
c) (a + b) (c + d)
d) 0
Explanation:
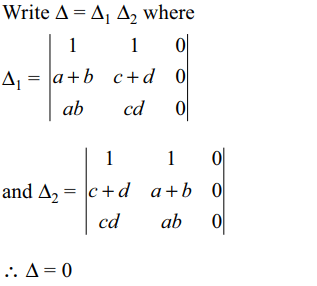
6. If \[\theta\epsilon R\] maximum value of \[\triangle=\begin{bmatrix}1 & 1 & 1\\1 & 1+\sin\theta & 1 \\1 & 1 & 1+\cos\theta\end{bmatrix}\]
is
a) 1/2
b) \[\sqrt{3}/2\]
c) \[\sqrt{2}\]
d) \[3\sqrt{2}/4\]
Explanation:
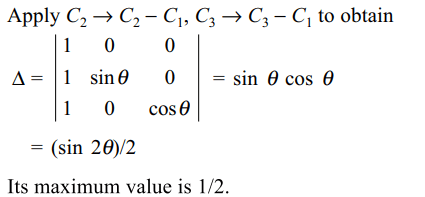
7. if \[\triangle=\begin{bmatrix}x+a& b & c\\a & x+b & c \\a & b & x+c\end{bmatrix}=0\]
then x equals
a) a + b + c
b) – (a + b + c)
c) 0, a + b + c
d) 0, – (a + b + c)
Explanation: Use C1 \[\rightarrow\] C1 + C2 + C3
8. The determinant \[\triangle=\begin{bmatrix}\sec^{2} \theta& \tan^{2}\theta & 1\\\tan^{2}\theta & \sec^{2}\theta & -1 \\12 & 10 & 2\end{bmatrix}\]
equals
a) \[2\sin^{2} \theta\]
b) \[12\sec^{2} \theta-10\tan^{2} \theta\]
c) \[12\sec^{2} \theta-10\tan^{2} \theta+5\]
d) 0
Explanation: Use C1 \[\rightarrow\] C1 - C2
9.Let f and g be two function defined on R such that
f(x + y) = f(x) g(y) + g(x) f(y) for each x, \[y\epsilon R\] . Let
\[\triangle=\begin{bmatrix}f\left(\theta+\alpha\right)& f\left(\alpha\right) & g\left(\alpha\right)\\f\left(\theta+\beta\right)& f\left(\beta\right) & g\left(\beta\right) \\f\left(\theta+\gamma\right) & f\left(\gamma\right) & g\left(\gamma\right)\end{bmatrix}\]
then \[\triangle\] equal
a) \[f(\alpha) f(\beta) f(\gamma)\]
b) \[g(\alpha) g(\beta) g(\gamma)\]
c) \[f(\alpha) g(\alpha) + f(\beta) g(\beta) + f(\gamma) g(\gamma)\]
d) 0
Explanation:
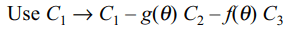
10. If a, \[b\epsilon R\] and \[\triangle=\begin{bmatrix}a & a+bi & bi \\a+bi & bi & a \\bi & a & a+bi \end{bmatrix}\]
then \[\triangle\] equals
a) \[a^{3}+b^{3}i\]
b) \[2\left(a^{3}+b^{3}\right)\]
c) \[a^{3}-b^{3}i\]
d) \[-2\left(a^{3}-b^{3}i\right)\]
Explanation: Use C1 \[\rightarrow\] C1 + C2 + C3