1.If A is matrix of size \[n \times n\] such that \[A^{2}+A+2I=O\] , then
a) A is non-singular
b) \[ A\neq O\]
c) \[\mid A\mid\neq 0\]
d) All of the above
Explanation: We have A(A + I) = – 2I
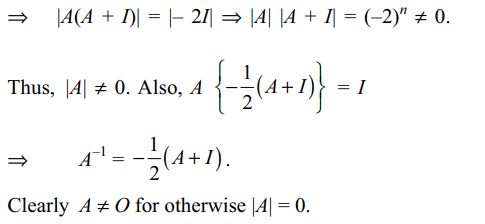
2. Let \[\alpha=\pi/5\] and \[A=\begin{bmatrix}\cos\alpha & \sin\alpha \\-\sin\alpha & \cos\alpha \end{bmatrix}\]
then \[B=A+A^{2}+A^{3}+A^{4}\]
is
a) singular
b) non-singular
c) skew-symmetric
d) Both b and c
Explanation:
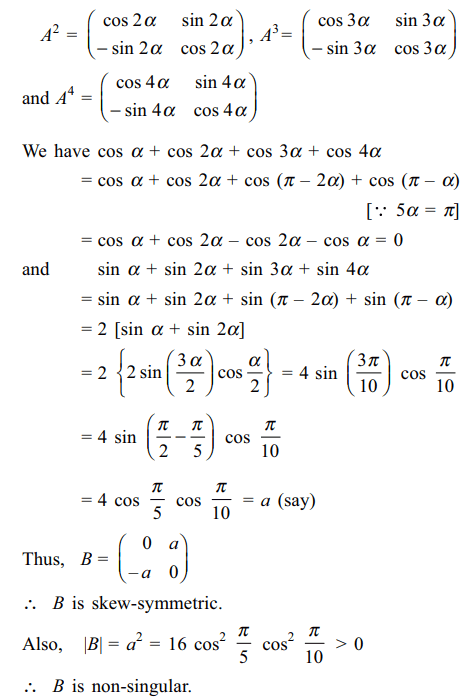
3. Let A, B be two \[2 \times2\] matrices.
Let \[\alpha= det\left(A\right) + det\left(B\right) – det\left(A + B\right)\]
and \[\beta= tr\left(AB\right) -\left(trA\right)\left(trB\right)\] , then
a) \[\alpha= \beta\]
b) \[\alpha+ \beta=0\]
c) \[\alpha^{2}= \beta\]
d) \[\alpha= \beta^{2}\]
Explanation:
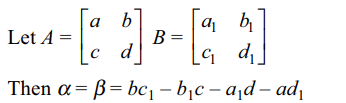
4. Let A be a \[3 \times3\] matrix with real entries such that
sum of the entries in each column of A is 1, then sum
of the entries of \[A^{2018}\] is
a) 1
b) 3
c) 2018
d) 6054
Explanation:
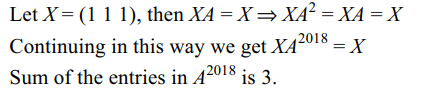
5. If \[A=\begin{bmatrix}0 & -1 & 2 \\1 & 0 & 3 \\-2 & -3 & 0\end{bmatrix}\]
then A + 2A' equals
a) A
b) A'
c) -A'
d) 2A
Explanation: Use A = - A'
6. Let \[A_{t}=\begin{bmatrix}1 & 3 & 2 \\2 & 5 & t \\4 & 7-t & -6\end{bmatrix}\]
then the value(s) of t for
which inverse of \[A_{t}\] does not exist.
a) -2,1
b) 3,2
c) 2,-3
d) 3,-1
Explanation: Set |At| = 0
7. Let a, b, \[c\epsilon R\] be such that a + b + c > 0 and abc = 2. Let
\[A=\begin{bmatrix}a & b & c \\b & c & a \\c & a & b\end{bmatrix}\]
If \[A^{2}=I\] , then value of \[a^{3}+b^{3}+c^{3}\] is
a) 7
b) 2
c) 0
d) -1
Explanation:
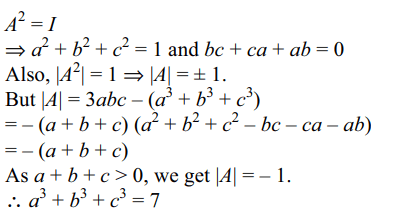
8. If a is a \[3 \times3\] skew summertic matrix with real
entries and trace of \[A^{2}\] equals zero, then
a) A = O
b) 2A = I
c) A is orthogonal
d) none of these
Explanation:
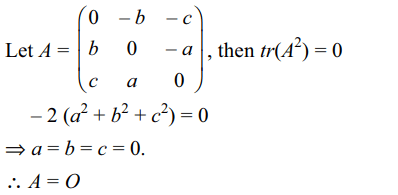
9. If \[\begin{bmatrix}i & 0 \\3 & -i \end{bmatrix}+X=\begin{bmatrix}i & 2 \\3 & 4+i \end{bmatrix}\]
– X, then X is equal to
a) \[\begin{bmatrix}0 & -1 \\3 & i \end{bmatrix}\]
b) \[\begin{bmatrix}0 & 1 \\0 & 2+i \end{bmatrix}\]
c) \[\begin{bmatrix}1 & 0 \\0 & 2-i \end{bmatrix}\]
d) none of these
Explanation:
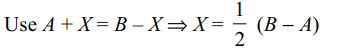
10. If \[A=\begin{bmatrix}0 & -i \\i & 0 \end{bmatrix},B=\begin{bmatrix}1 & 0 \\0 & -1 \end{bmatrix}\] ,
then AB + BA is
a) null matrix
b) unit matrix
c) invertible matrix
d) none of these
Explanation: Calculate directly