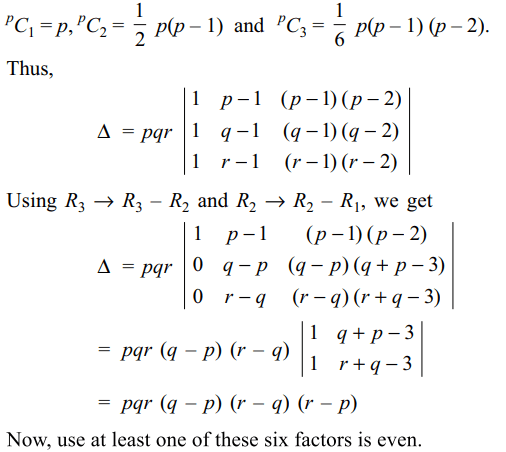1. Suppose a, b, c, x, y, z > 0 and satisfy the
system of linear equations
cy + bz = a
cx + az = b
bx + ay = c
then
a) a, b, c are sides of an acute angled triangle
b) x, y, z are cosines of the angles of an acute
angled triangle
c) Each of x, y, z < 1
d) All of the above
Explanation:

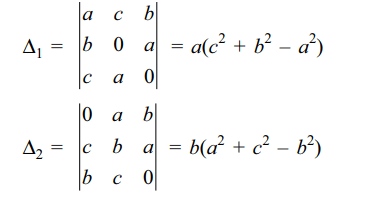
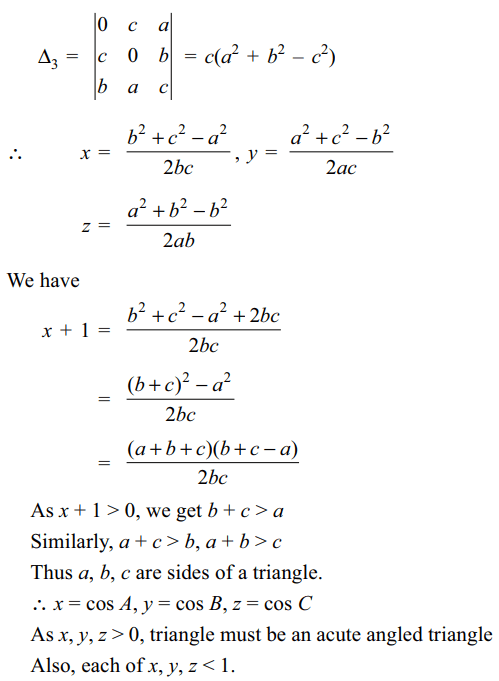
2. For \[\theta\epsilon\left[0,2\pi\right]\] , let \[\triangle\left(\theta\right)=\begin{bmatrix}\cos\theta & \cos2\theta & \cos3\theta \\\cos2\theta & \cos3\theta & \cos4\theta \\\cos3\theta & \cos4\theta & \cos5\theta\end{bmatrix}\]
then
a) \[\triangle\left(\frac{5\pi}{12}\right)=0\]
b) \[\triangle\left(\frac{7\pi}{12}\right)=-1\]
c) \[\triangle\left(\frac{2\pi}{3}\right)=0\]
d) Both a and c
Explanation: Put z = cos \[\theta\] + isin \[\theta\] , then
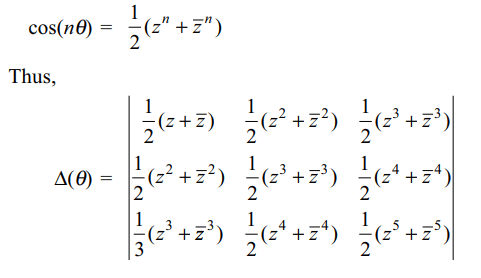
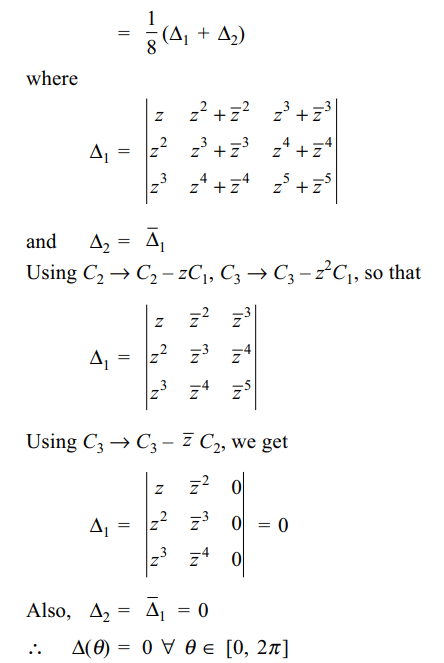
3. The determinant
\[\triangle=\begin{bmatrix}a & b & a\alpha+b \\b & c & b\alpha+c \\a\alpha+b & b\alpha+c & 0\end{bmatrix}\]
is equal to zero if
a) a, b, c are in A.P
b) a, b, c are in G.P.
c) \[\alpha\] is a root of \[ax^{2}+2bx+c=0\]
d) Both b and c
Explanation:
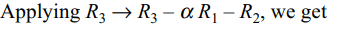
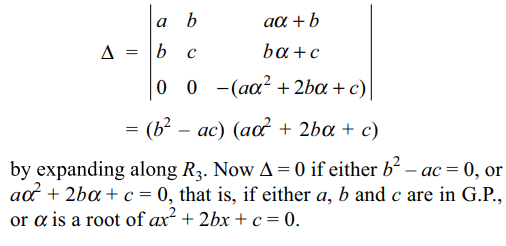
4. If \[\triangle(x)=\begin{bmatrix}x^{2}-5x+3 &2x-5 & 3 \\3x^{2}+x+4 & 6x+1 & 9 \\7x^{2}-6x+9 & 14x-6 & 21\end{bmatrix}=ax^{3}+bx^{2}+cx+d\]
then
a) a = 0
b) b = 0
c) c = 0
d) All of the above
Explanation: Differentiate both the sides with respect to x
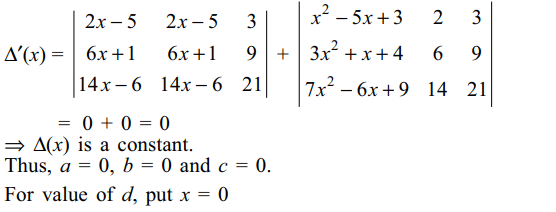
5. If \[\triangle=\begin{bmatrix}1/z & 1/z & -\left(x+y\right)/z^{2} \\-\left(y+z\right)/x^{2} & 1/x & 1/x \\-y\left(y+z\right)/x^{2}z & \left(x+2y+z\right)/xz & -\left(x+y\right)/xz^{2}\end{bmatrix}\]
then
a) \[\triangle\] is independent of x
b) \[\triangle\] is independent of y
c) \[\triangle=0\]
d) All of the above
Explanation: Multiplying C1 by x, C2 by y and C3 by z,
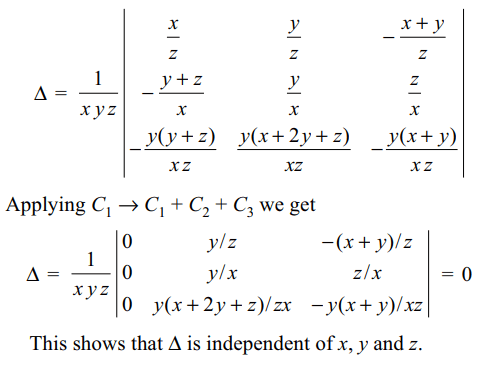
6. Let \[\triangle=\begin{bmatrix}\sin\theta\cos\phi & \sin\theta\sin\phi & \cos\theta \\\cos\theta\cos\phi & \cos\theta\sin\phi & -\sin\theta \\-\sin\theta\sin\phi & \sin\theta\cos\phi & 0\end{bmatrix}\]
then
a) \[\triangle\] is independent of \[\theta\]
b) \[\triangle\] is independent of \[\phi\]
c) \[\frac{d\triangle}{d\theta}\mid_{\theta =\pi/2}=0\]
d) Both b and c
Explanation:
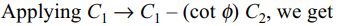
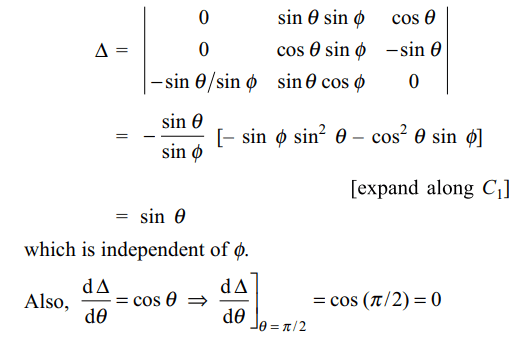
7. Let \[\triangle=\begin{bmatrix}\frac{1}{\sin\theta\cos\phi} & \frac{1}{\sin\theta\sin\phi} & \frac{1}{\cos\theta} \\\frac{-\cos \theta}{\sin^2\theta\cos\phi} & \frac{-\cos \theta}{\sin^2\theta\sin\phi} & \frac{\sin\theta}{\cos^2\theta} \\ \frac{\sin\phi}{\sin\theta\cos^2\phi }& \frac{-\cos\phi}{\sin\theta\sin^2\phi} & 0\end{bmatrix}\]
a) \[\triangle\] is dependent on \[\theta\]
b) \[\triangle\] is dependent on \[\phi\]
c) \[\triangle\] is a constant
d) Both a and b
Explanation: Taking 1/sin \[\theta\] cos \[\phi\] , 1/sin \[\theta\] sin \[\phi\] , 1/cos \[\theta\] common from C1, C2, C3 respectively, we get
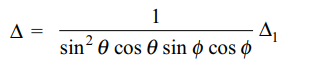
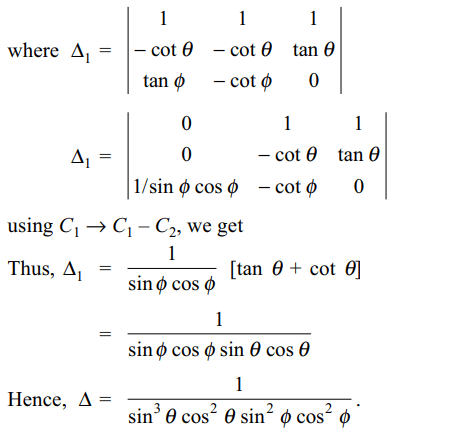
8. The determinant \[\triangle=\begin{bmatrix}a^{2}+x & ab & ac \\ab & b^{2} +x& bc \\ac & bc & c^{2}+x\end{bmatrix}\]
is divisible by
a) x
b) \[x^{2}\]
c) \[a^{2}+b^{2}+c^{2}+x\]
d) All of the above
Explanation: We can write \[\triangle\] as
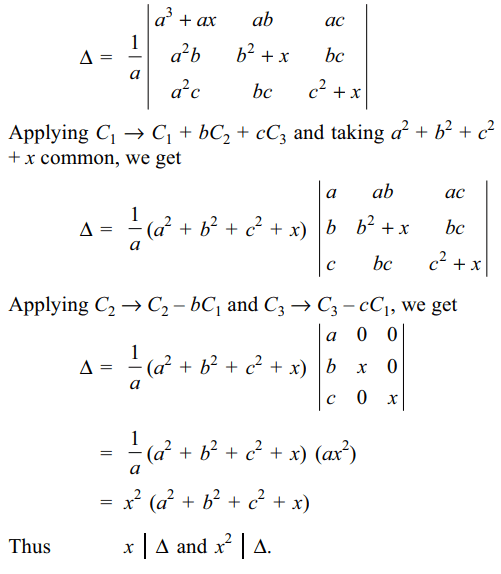
9. Let f(x) \[=\begin{bmatrix}\frac{\pi^{n}}{x} & \sin\pi x & \cos\pi x \\\left(-1\right)^{n}n! & -\sin\left(\frac{n\pi}{2}\right) & -\cos\left(\frac{n\pi}{2}\right) \\-1 & \frac{1}{\sqrt{2}} & \frac{\sqrt{3}}{2}\end{bmatrix}\]
then value of \[\frac{d^{n}}{dx^{n}}\] [f(x)] at x = 1 is
a) 0
b) independent of x
c) \[\frac{1}{\sqrt{2}}\]
d) Both a and b
Explanation:
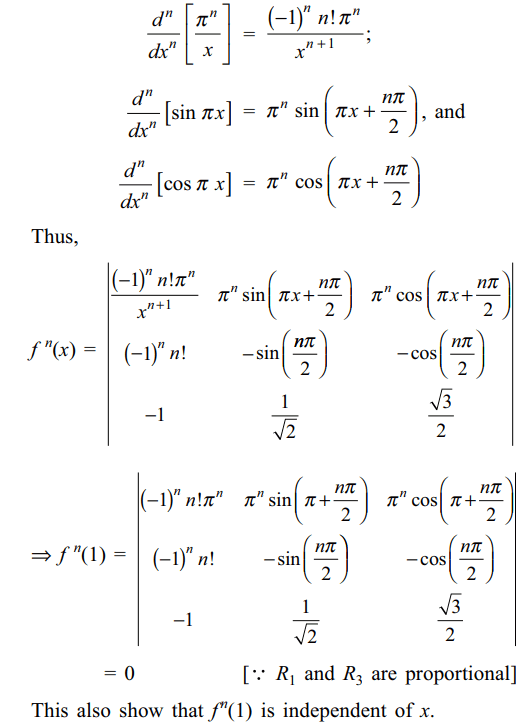
10. If p, q and r are positive integers, and \[\triangle=12\begin{bmatrix}^{p}C_{1} & ^{p}C_{2} & ^{p}C_{3} \\^{q}C_{1} & ^{q}C_{2} & ^{q}C_{3} \\^{r}C_{1} & ^{r}C_{2} & ^{r}C_{3}\end{bmatrix}\]
then
a) \[\triangle\] is an even integer
b) \[\triangle\] is divisible by 12
c) \[\triangle\] is an rational number
d) Both a and c
Explanation: