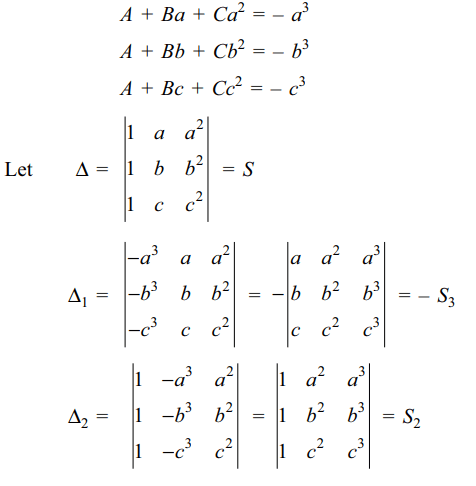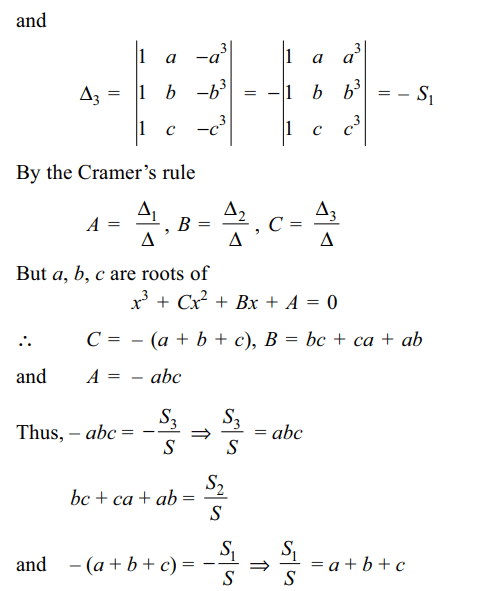1. For a fixed positive integer n, let
\[D=\begin{bmatrix}\left(n-1\right)! & \left(n+1\right)! & \left(n+3\right)!/n\left(n+1\right)\\\left(n+1\right)! & \left(n+3\right)! & \left(n+5\right)!/\left(n+2\right)\left(n+3\right) \\\left(n+3\right)! & \left(n+5\right)! & \left(n+7\right)!/\left(n+4\right)\left(n+5\right)\end{bmatrix}\]
then \[\frac{D}{\left(n-1\right)!\left(n+1\right)!\left(n+3\right)!}\] is equal to
a) -8
b) -16
c) -32
d) -64
Explanation: Taking (n – 1)! common from R1, (n + 1)! from R2 and (n + 3)! from R3, we get
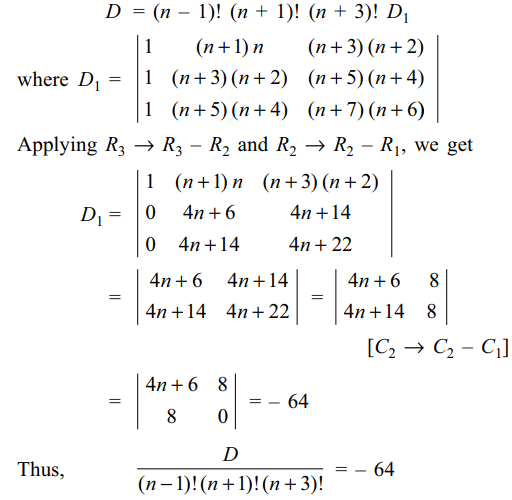
2. If \[\triangle=\begin{bmatrix}\sqrt{6} & 2i & 3+\sqrt{6} \\\sqrt{12} & \sqrt{3}+\sqrt{8}i& 3\sqrt{2}+\sqrt{6}i \\ \sqrt{18} & \sqrt{2}+\sqrt{12}i & \sqrt{27}+2i\end{bmatrix}\]
then \[\triangle\] is
a) a natural number
b) a negative integer
c) an irrational number
d) an imaginary number
Explanation:
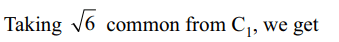
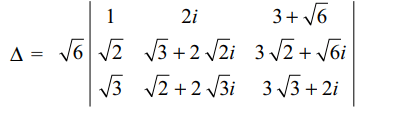
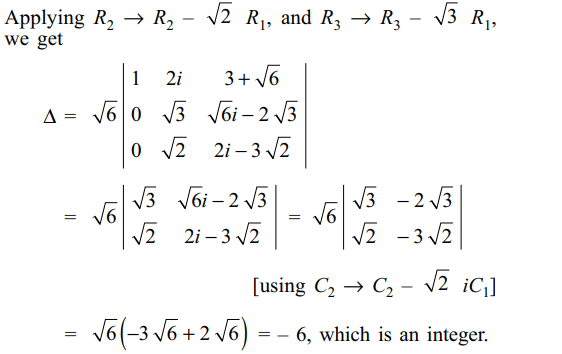
3. If x, y, z are different from zero and \[\triangle=\begin{bmatrix}a & b-y & c-z \\a-x & b & c-z \\a-x & b-y & c\end{bmatrix}=0\]
then the value of the expression \[\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\] is
a) 0
b) -1
c) 1
d) 2
Explanation:
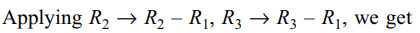
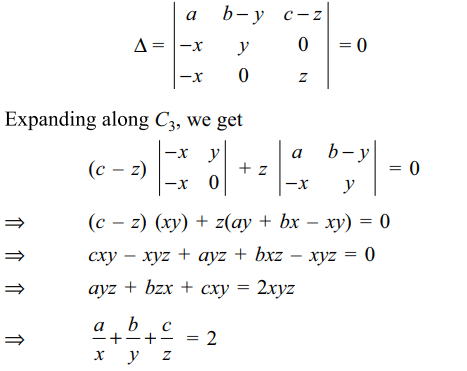
4. Let \[f\left(x\right)=\begin{bmatrix}\cos x & x & 1 \\2\sin x & x^{2} & 2x \\\tan x & x &2\end{bmatrix}\]
\[\lim_{x \rightarrow 0}\frac{f\left(x\right)}{x^{2}}\] is equal to
a) -1
b) 0
c) 2
d) 3
Explanation: : For x \[\neq\] 0, we have
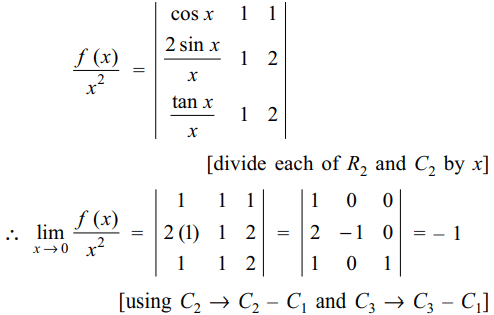
5. If \[ p \neq a, q\neq b, r\neq c\] and the system of
equations
px + ay + az = 0
bx + qy + bz = 0
cx + cy + rz = 0
has a non-trivial solution, then the value of
\[\frac{p}{p-a}+\frac{q}{q-b}+\frac{r}{r-c}\]
a) -1
b) 0
c) 1
d) 2
Explanation: As the given system of equations has a non-trivial solution
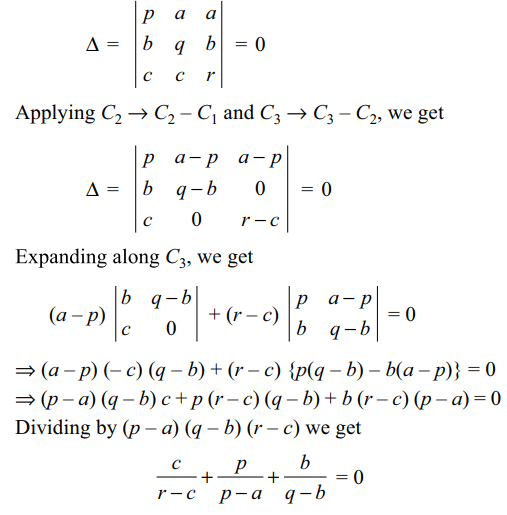
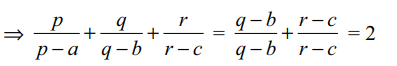
6. If \[p\neq 0\] , solution set of the equation
\[\triangle=\begin{bmatrix}1 & 1 & x \\p+1 & p+1 & p+x \\3 & x+1 & x+2\end{bmatrix}=0\]
is
a) {1, 2}
b) {2, 3}
c) {1, p, 2}
d) {1, 2, – p}
Explanation: Applying C2 \[\rightarrow\] C2 – C1, we get
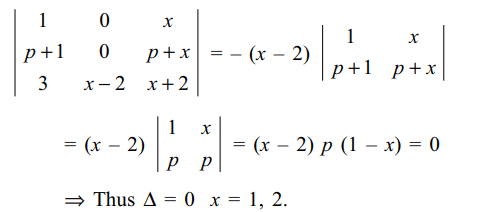
7. Let a, b, \[c\epsilon R\] be such that \[a+b+c\neq 0\] . If the system of equations
ax + by + cz = 0
bx + cy + az = 0
cx + ay + bz = 0
has a non-trivial solution, then
a) a + c – b = 0
b) b + c – a = 0
c) a + b – c = 0
d) a = b = c
Explanation: As the system of equations has a non-trivial solution,
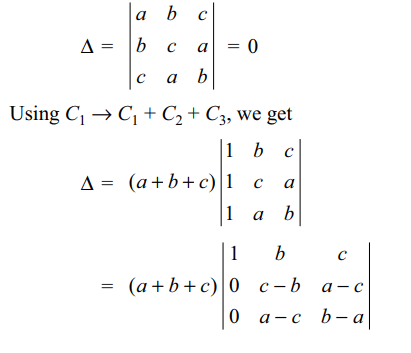
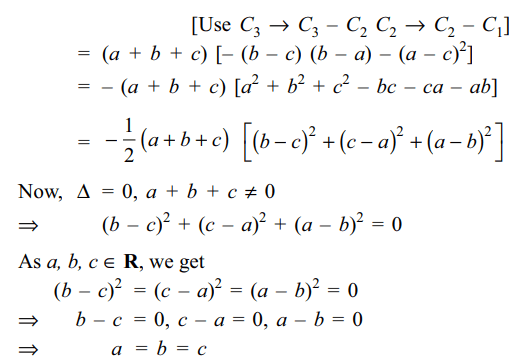
8. If the system of linear equations x + y + z
= 6, x + 2y + 3z = 14 and \[2x+5y+\lambda z=\mu\left(\lambda,\mu\epsilon R\right)\]
has
a unique solution, then
a) \[\lambda\neq 8\]
b) \[\lambda=8,\mu\neq 36\]
c) \[\lambda=8,\mu=36\]
d) none of these
Explanation: The given system of linear equations has a unique solution if
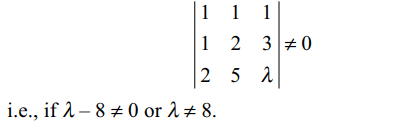
9. Let \[A\left(z_{1}\right)\] , \[B\left(z_{2}\right)\] and \[C\left(z_{3}\right)\] be the vertices
of a triangle. Let a = BC, b = CA and c = AB, then
\[b\begin{bmatrix}z & \bar{z} & 1 \\z_{1} & \bar{z_{1}} & 1 \\z_{2} & \bar{z_{2}} & 1\end{bmatrix}+c\begin{bmatrix}z & \bar{z} & 1 \\z_{1} & \bar{z_{1}} & 1 \\z_{3} & \bar{z_{3}} & 1\end{bmatrix}=0\]
represents
a) median of \[\triangle ABC\] through A
b) angle bisector of \[\angle A\]
c) altitude of \[\triangle ABC\] through A
d) perpendicular bisector of side BC
Explanation:
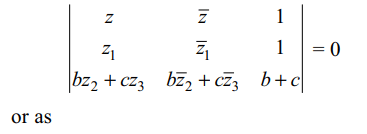
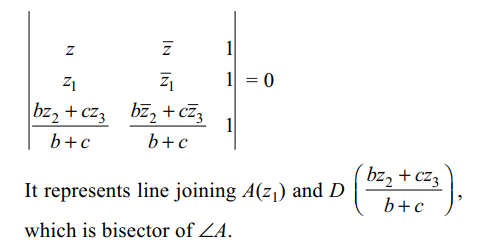
10. Suppose a, b, c are distinct real numbers
and let
\[S=\begin{bmatrix}1 & a & a^{2} \\1 & b & b^{2} \\1 & c & c^{2}\end{bmatrix} S_{1}=\begin{bmatrix}1 & a & a^{3} \\1 & b & b^{3} \\1 & c & c^{3}\end{bmatrix} S_{2}=\begin{bmatrix}1 & a^{2} & a^{3} \\1 & b^{2} & b^{3} \\1 & c^{2} & c^{3}\end{bmatrix} S_{3}=\begin{bmatrix}a & a^{2} & a^{3} \\b & b^{2} & b^{3} \\c & c^{2} & c^{3}\end{bmatrix}\]
then
a) \[\frac{s_{1}}{s}=a+b+c\]
b) \[\frac{s_{2}}{s}=ab+bc+ca\]
c) \[\frac{s_{3}}{s}=abc\]
d) All of the above
Explanation: