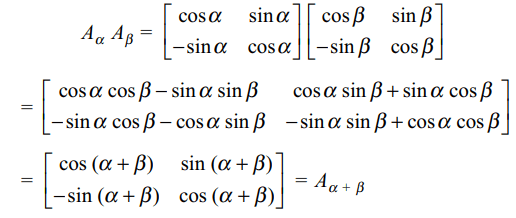1. Let \[A=\left(\begin{array}{c}a & b\\ c & d\end{array}\right)\]
be such that \[A^{3}=O\] , but
\[A\neq O\] , then
a) \[A^{2}=O\]
b) \[A^{2}=A\]
c) \[A^{2}=I-A\]
d) none of these
Explanation: As A3 = O, we get |A3| = 0
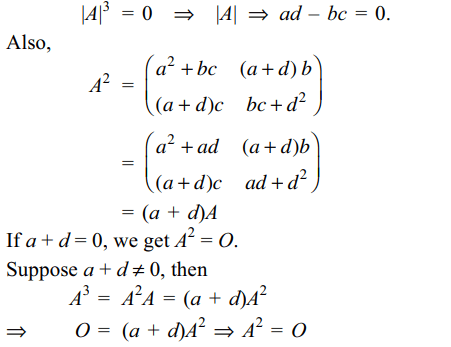
2. Let S be the set of all real matrices
\[A =\begin{bmatrix}a & b \\c & d \end{bmatrix}\]
such that a + d = 3 and \[A'=A^{2}-3A\] . Then S:
a) is an empty set
b) has exactly one element
c) has exactly two elements
d) has exactly four elements
Explanation:
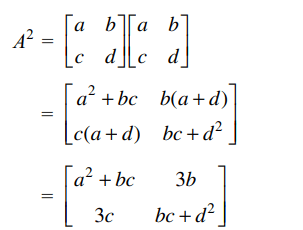
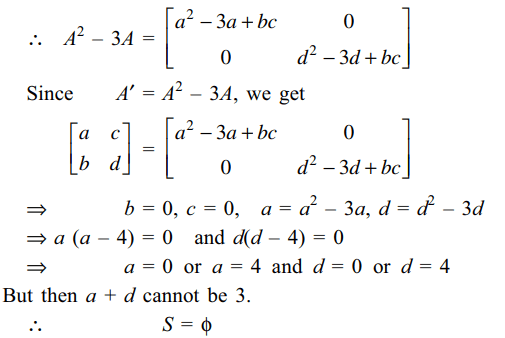
3. Let \[A =\begin{bmatrix}a & b \\c & d \end{bmatrix}\] , be a 2 × 2 matrix where
a, b, c, \[d \epsilon\] {0, 1}. The number of such matrices which have
inverse is
a) 5
b) 6
c) 7
d) 8
Explanation: det(A) = ad – bc
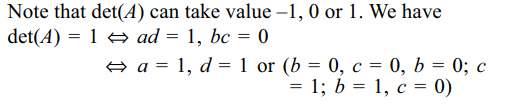
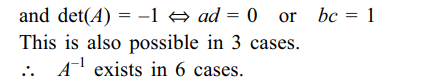
4. Let \[A =\begin{bmatrix}a & b \\c & d \end{bmatrix}\] , where a, b, c, d \[ \epsilon R\] . If
\[A -\alpha I\] is invertible for all a \[\alpha \epsilon\] R, then
a) bc > 0
b) bc=0
c) \[bc> min\left(0,\frac{1}{2}ad\right)\]
d) a=0
Explanation: As A – \[\alpha\] I is invertible for all a \[\epsilon\] R
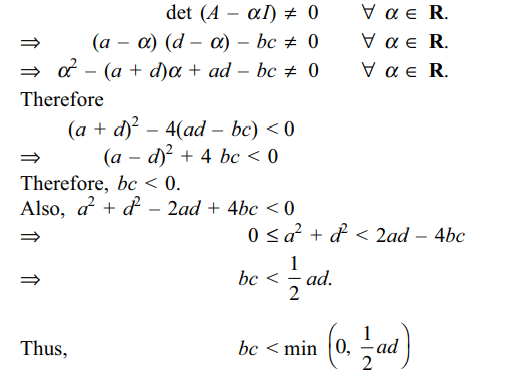
5. If A + B is a non-singular matrix, then
\[A – B – A \left(A + B\right)^{-1}A + B(A + B)^{-1} B\]
equals
a) O
b) I
c) A
d) B
Explanation:
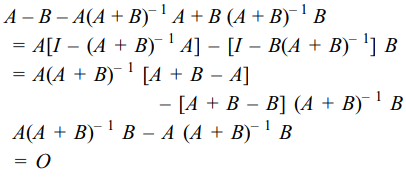
6. If P is a 3 * 3 matrix such that
P' = 2P + I, then there exists a column matrix
\[X=\left(\begin{array}{c}x\\ y \\ z \end{array}\right)\neq O\]
such that
a) PX = O
b) PX = X
c) PX = 2X
d) PX = -X
Explanation:
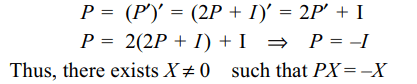
7. Let P and Q be \[ 3\times 3\] matrices with \[P\neq Q\]
If \[ P^{3}=Q^{3}\] and \[ P^{2}Q=Q^{2}P\] , then determinant of \[ \left(P^{2}+Q^{2}\right)\]
is equal to
a) 1
b) 0
c) -1
d) -2
Explanation:
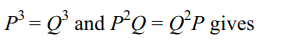
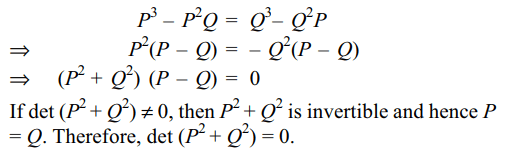
8. Let \[P=\begin{bmatrix}1 & 0 & 0 \\9 & 1 & 0 \\27 & 9 & 1 \end{bmatrix}\]
and \[Q=\left[q_{ij}\right]_{3\times 3}\]
be such that \[P^{5}-Q=I\] , then \[\frac{q_{21}+q_{31}}{q_{32}}\] is equal to
a) 22
b) 33
c) 44
d) 55
Explanation: Write P = I + R where
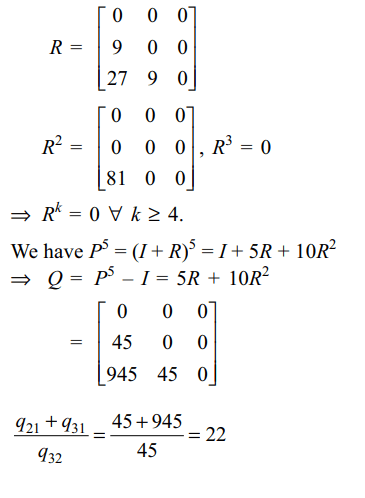
9. Let \[a_{ij}=\left(2+\sqrt{3}\right)^{i+j}+\left(2-\sqrt{3}\right)^{i+j},1 \leq i, j \leq3\]
and let \[A=\left(a_{ij}\right)_{3\times 3}\] , then det (A) is equal to
a) 1
b) \[\left(2+\sqrt{3}\right)^{9}\]
c) \[\left(2-\sqrt{3}\right)^{9}\]
d) 0
Explanation: For n \[\epsilon\] N
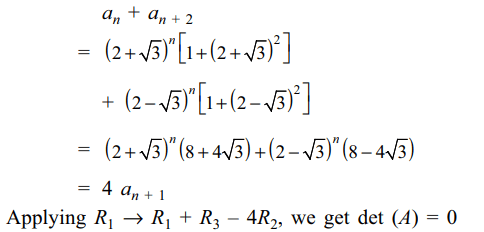
10. If \[A_{\alpha}=\begin{bmatrix}\cos \alpha & \sin\alpha \\-\sin\alpha & \cos\alpha \end{bmatrix}\] , then
\[A_{\alpha}A_{\beta}\] is equal to
a) \[A_{\alpha+\beta}\]
b) \[A_{\alpha\beta}\]
c) \[A_{\alpha-\beta}\]
d) none of these
Explanation: