PrepBharat

1. If \[pqr\neq0\]  and the system of equations
(p + a)x + by + cz = 0
ax + (q + b)y + cz = 0
ax + by + (r + c)z = 0
has a non-trivial solution, then value of \[\frac{a}{p}+\frac{b}{q}+\frac{c}{r}\]     is
a) -1
b) 0
c) 1
d) 2

View Answer

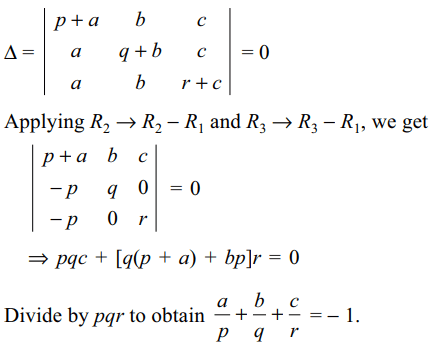
2. Let \[a = 2^{A}, b = 2^{B}, C = 2^{C}\]     the system of equations
ax + by + (a \[\alpha\] + b)z = 0
bx + cy + (b \[\alpha\] + c)z = 0
(a \[\alpha\] + b)x + (b \[\alpha\] + c)y = 0
has a non-zero solutions if A, B, C are in
a) A.P
b) G.P
c) H.P
d) none of these

View Answer

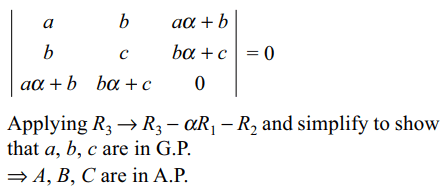
3. If the system of equations
ax + ay – z = 0
bx – y + bz = 0
– x + cy + cz = 0
(where \[a, b, c \neq – 1\]   ) has a non-trivial solution, then value of \[\frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}\]     is
a) 2
b) -1
c) -2
d) 0

View Answer

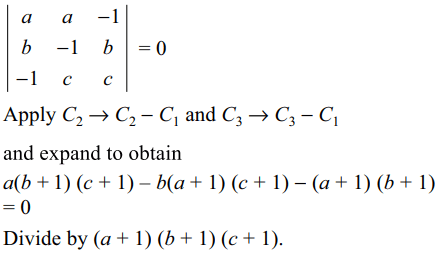
4. All the values of \[\lambda\] for which the system of equations
\[\left(\lambda + 5\right)x + \left(\lambda – 4\right)y + z = 0\]
\[\left(\lambda - 2\right)x + \left(\lambda + 3\right)y + z = 0\]
\[\lambda x+\lambda y+z=0\]
has a non-trivial solution lie in the set
a) {– 1, 2}
b) {0, – 1}
c) {0}
d) R

View Answer

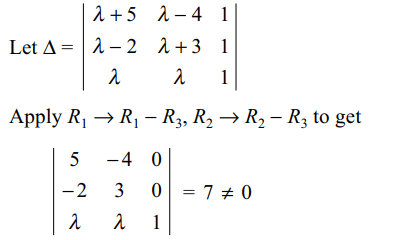
5. Given the system of equations
(b + c) (y + z) – ax = b – c
(c + a) (z + x) – by = c – a
(a + b) (x + y) – cz = a – b
(where \[a + b + c \neq 0\]   ); then x : y : z is given by
a) b – c : c – a : a – b
b) b + c : c + a : a + b
c) a : b : c
d) \[\frac{a}{b}:\frac{b}{c}:\frac{c}{a}\]

View Answer

6. Number of real values of \[\lambda\] for which the system of equations
\[\left(\lambda + 3\right)x + \left(\lambda + 2\right)y + z = 0\]
\[3x + \left(\lambda + 3\right)y + z = 0\]
2x + 3y + z = 0
has a non-trivial solutions is
a) 0
b) 1
c) 2
d) Infinite

View Answer

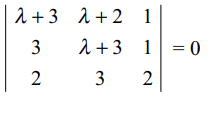
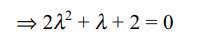
7. The value of \[\lambda\] for which the system of equations
2x – y – 2z = 2
x – 2y + z = – 4
\[x+y+\lambda z=4\]
has no solution is
a) 3
b) -3
c) 2
d) -2

View Answer

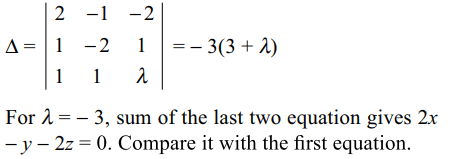
8. The determinant \[\begin{bmatrix}\sin\alpha & \cos\alpha & 1 \\\sin\beta & \cos\beta & 1 \\\sin\gamma & \cos\gamma & 1\end{bmatrix}\]         is equals to
a) \[-4\sin\frac{\alpha-\beta}{2}\sin\frac{\beta-\gamma}{2}\sin\frac{\gamma-\alpha}{2}\]
b) \[\sin\alpha+\sin\beta+\sin\gamma\]
c) \[\sin\left(\alpha-\beta\right)+\sin\left(\beta-\gamma\right)+\sin\left(\gamma-\alpha\right)\]
d) Both a and c

View Answer

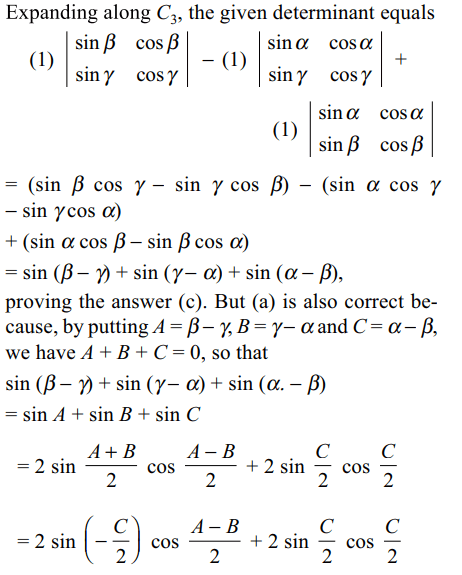
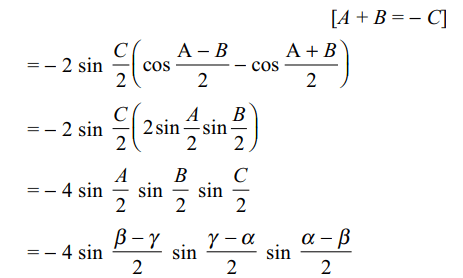
9. If a, b, c > 0 and x, y, \[z\epsilon R\] , then the determinant \[\begin{bmatrix}\left(a^{x}+a^{-x}\right)^{2} & \left(a^{x}-a^{-x}\right)^{2} & 1 \\\left(b^{y}+b^{-y}\right)^{2} & \left(b^{y}-b^{-y}\right)^{2} & 1 \\\left(c^{z}+c^{-z}\right)^{2} & \left(c^{z}-c^{-z}\right)^{2} & 1\end{bmatrix}\]
is indepenent of
a) a, b, c
b) x, y, z
c) a, b, c, x, y, z
d) All of the above

View Answer

10. If \[a\neq b\]  , the equation \[\begin{bmatrix}x & a & a \\a & x & a \\a & a & x\end{bmatrix}+\begin{bmatrix}b & b & x \\b & x & b \\x & b & b\end{bmatrix}=0\]
is satisfied when x equals
a) 0
b) a-b
c) a+b
d) \[\frac{2}{3}\frac{a^{2}+ab+b^{2}}{a+b}\]

View Answer