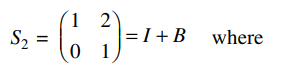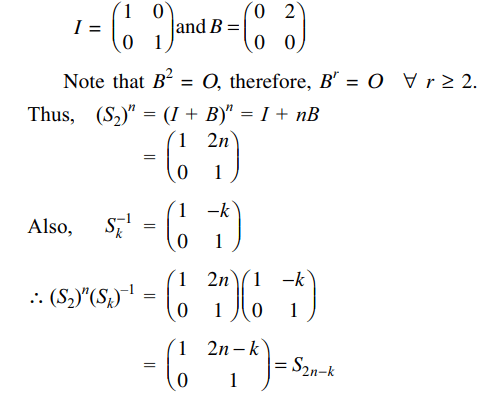1. If \[A\left(\theta\right)=\left(\begin{array}{c}1 & \tan\theta\\ -\tan\theta & 1\end{array}\right)\]
and AB = I,
then \[\left(sec^{2}\theta\right)B\] is equal to
a) \[A\left(\theta\right)\]
b) \[A\left(-\theta\right)\]
c) \[A\left(\theta/2\right)\]
d) \[A\left(-\theta/2\right)\]
Explanation: As AB = I, we get B = A-1
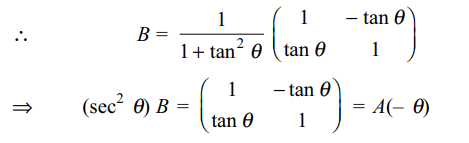
2. if \[A=\begin{bmatrix}a & b \\b & a \end{bmatrix}\] and \[A^{2}=\begin{bmatrix}\alpha & \beta \\\beta & \alpha \end{bmatrix}\]
then
a) \[\alpha =a^{2}+b^{2},\beta=2ab\]
b) \[\alpha =a^{2}+b^{2},\beta=a^{2}-b^{2}\]
c) \[\alpha =2ab ,\beta=a^{2}+b^{2}\]
d) \[\alpha =a^{2}+b^{2},\beta=ab\]
Explanation:
3. If \[A=\begin{bmatrix}a & b \\c & d \end{bmatrix}\]
is such that |A| = 0 and
\[A^{2}-\left(a+d\right)A+kI=O\] , then k is equal to
a) b+c
b) a+d
c) ab+cd
d) 0
Explanation: As |A| = 0, we get ad – bc = 0
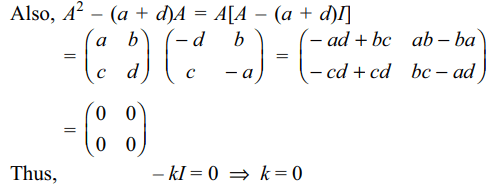
4. If \[A=\begin{bmatrix}\alpha & 2 \\2 & \alpha \end{bmatrix}\] and \[\mid A^{3}\mid =125\] , then \[\alpha\] is
equal to
a) \[\pm 3\]
b) \[\pm 2\]
c) \[\pm 5\]
d) 0
Explanation: We have 125 = |A3| = |A|3
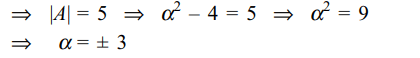
5. If \[ A=\begin{bmatrix}a+ib & c+id \\-c+id & a-ib \end{bmatrix}\] and \[a^{2}+b^{2}+c^{2}+d^{2}=1\] , then \[A^{-1}\] is equal to
a) \[ \begin{bmatrix}a+ib & -c+id \\-c+id & a-ib \end{bmatrix}\]
b) \[ \begin{bmatrix}a-ib & c-id \\-c-id & a+ib \end{bmatrix}\]
c) \[ \begin{bmatrix}a-ib & -c-id \\c-id & a+ib \end{bmatrix}\]
d) none of these
Explanation:
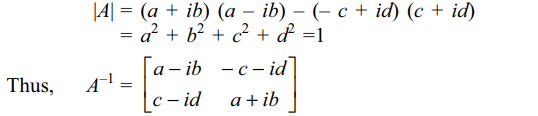
6. The number of values of k for which the
system of equations
(k + 1)x + 8y = 4k, kx + (k + 3)y = 3k – 1
has no solution is
a) 0
b) 3
c) 2
d) 1
Explanation: For the system of equations to have no solution, we must have

7. if \[ \begin{bmatrix}\cos\left(\pi/6\right) & \sin\left(\pi/6\right) \\-\sin\left(\pi/6\right) & \cos\left(\pi/6\right) \end{bmatrix}A=\begin{bmatrix}1 & 1 \\0 & 1 \end{bmatrix}\]
and Q=PAP' then \[P'Q^{2019}P\] is equal to
a) \[\begin{bmatrix}1 & \sqrt{3}/2 \\0 & 2019 \end{bmatrix}\]
b) \[\begin{bmatrix}1 & 2019 \\0 & 1 \end{bmatrix}\]
c) \[\begin{bmatrix}\sqrt{3}/2 & 2019 \\0 & 1 \end{bmatrix}\]
d) \[\begin{bmatrix}\sqrt{3}/2 & -1/2 \\1 & 2019 \end{bmatrix}\]
Explanation:
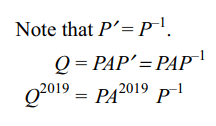
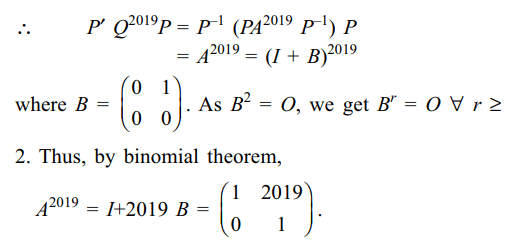
8.If \[A=\begin{bmatrix}a_{1} & b_{1} & c_{1} \\a_{2} & b_{2} & c_{2} \\a_{3} & b_{3} & c_{3}\end{bmatrix}\]
and \[\mid A\mid \neq 0\] , then the
system of equations \[a_{1}x+b_{1}y+c_{1}z=0 , a_{2}x+b_{2}y+c_{2}z=0\] and \[a_{3}x+b_{3}y+c_{3}z=0\] has
a) only one solution
b) infinite number of solutions
c) no solution
d) More than one but finite number of solution
Explanation: Note that A is invertible as |A| \[\neq\] 0.
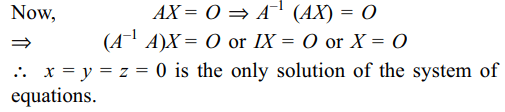
9. If \[\left(\begin{array}{c}1 & -\tan\theta\\ \tan\theta & 1\end{array}\right)\left(\begin{array}{c}1 & \tan\theta\\ -\tan\theta & 1\end{array}\right)^{-1}=\begin{bmatrix}a & -b \\b & a \end{bmatrix}\]
then
a) a = b = 1
b) \[a=\cos 2\theta, b=\sin 2\theta\]
c) \[a=\sin 2\theta, b=\cos 2\theta\]
d) \[a=1, b=\sin 2\theta\]
Explanation:
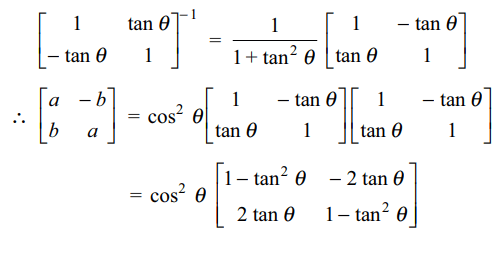
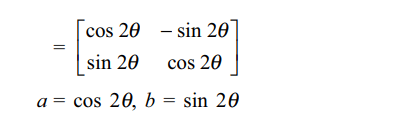
10. Let \[S_{k}=\left(\begin{array}{c}1 & k\\ 0 & 1\end{array}\right),k\epsilon N\]
then \[\left(S_{2}\right)^{n}\left(S_{k}\right)^{-1}\] (where \[n\epsilon N\]) is equal to:
a) \[S_{2n+k}\]
b) \[S_{2n-k}\]
c) \[S_{2^{n}+k-1}\]
d) \[S_{2^{n}-k}\]
Explanation: