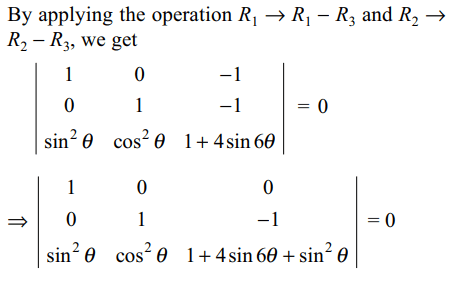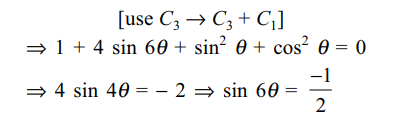1. If \[f\left(x\right)=\begin{bmatrix}\sin 2x\left(1+2\cos x\right) &\sin2x & \sin3x\\3+4\sin x & 3 & 4\sin x \\1+\sin x & \sin x & 1\end{bmatrix}\]
then the value of \[\int_{0}^{\pi/2} f\left(x\right) d(x)\] is
a) 3
b) 2/3
c) 1/3
d) 0
Explanation:
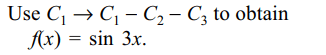
2. If \[\alpha,\beta,\gamma\] are the roots of \[x^{3}+ax^{2}+b=0\] , then the
determinant \[\triangle\] , where
\[\triangle=\begin{bmatrix}\alpha & \beta & \gamma \\\beta & \gamma & \alpha \\\gamma & \alpha & \beta\end{bmatrix}\]
equals
a) \[-a^{3}\]
b) \[a^{3}-3b\]
c) \[a^{2}-3b\]
d) a3
Explanation:
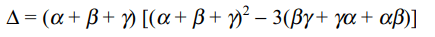
3. The number of distinct real roots of \[\triangle=\begin{bmatrix}\tan x & \cot x & \cot x \\\cot x & \tan x & \cot x \\\cot x & \cot x & \tan x\end{bmatrix}=0\]
in the interval\[-\pi/4\leq x \leq\pi/4\] is
a) 0
b) 2
c) 1
d) 3
Explanation:

4. If \[\omega \neq 1\] is a complex cube root of unity ,and \[x+iy =\begin{bmatrix}1 & i & -\omega \\-i & 1 & \omega^{2} \\\omega & -\omega^{2} & 1\end{bmatrix}\]
then
a) x = – 1, y = 0
b) x = 1, y = – 1
c) x = 1, y = 1
d) x = 0, y = 0
Explanation: Simplify to obtain x + iy = - 1
5. If \[e^{ix}=\cos x+i \sin x\] and \[x+iy=\begin{bmatrix}1 & e^{\pi i/4} & e^{\pi i/3} \\e^{-\pi i/4} & 1 & e^{2\pi i/3} \\e^{-\pi i/3} & e^{-2\pi i/3} & e^{2\pi i}\end{bmatrix}\]
then
a) \[x = – 1, y =\sqrt{2}\]
b) \[x = 1, y =-\sqrt{2}\]
c) \[x = – \sqrt{2}, y =\sqrt{2}\]
d) none of these
Explanation:
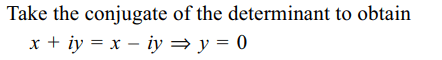
6. If a, b, \[c\epsilon R\] , the number of real roots of the
equation \[\triangle=\begin{bmatrix}x & c & -b \\-c & x & a \\b & -a & x\end{bmatrix} = 0\]
is
a) 0
b) 1
c) 2
d) 3
Explanation:
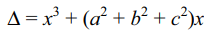
7. If a, b, \[c\epsilon R\] and a2+b2-ab-a-b+1 \[\leq\] 0
and \[\alpha+\beta+\gamma=0\] , then \[\triangle=\begin{bmatrix}1 & \cos\gamma & \cos\beta \\\cos\gamma & a & \cos\alpha \\\cos\alpha & \cos\beta & b\end{bmatrix}\]
equals
a) ab
b) 1
c) 2
d) 3
Explanation:

8. If \[\triangle=\begin{bmatrix}\sin\alpha &\cos \alpha&\sin\alpha+\cos\beta \\\sin\beta& \cos \alpha & \sin\beta+\cos\beta \\\sin\gamma & \cos \alpha & \sin\gamma+\cos\beta\end{bmatrix}\]
then \[\triangle\] is equal to
a) \[\sin\alpha\sin\beta\sin\gamma\]
b) \[\cos\alpha\sec\beta\tan\gamma\]
c) \[\sin\alpha\sin\left(\alpha+\beta\right)+\cos\alpha\cos\left(\gamma+\beta\right)\]
d) 0
Explanation:
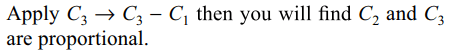
9. Let \[f\left(x\right)=\begin{bmatrix}cosec x & \sin x & cosec^2 x+\tan x \sec x \\\sin^{2}x & \sin^{2}x & \sec^{2}x \\1 & \sin^{2}x & \sin^{2}x\end{bmatrix}\]
then \[\int_{0}^{\pi/2} f\left(x\right) dx\] equals
a) \[-\left(\frac{\pi}{4}+\frac{8}{15}\right)\]
b) \[\frac{\pi}{4}\]
c) \[\frac{\pi}{4}+\frac{1}{5}\]
d) \[\pi\]
Explanation:
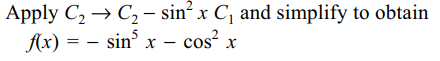
10. The values of \[\theta\] lying between \[\theta=0\] and \[\theta=\pi/2\] and
satisfying the equation \[\begin{bmatrix}1+\sin^{2}\theta & \cos^{2}\theta & 4\sin6\theta \\\sin^{2}\theta & 1+\cos^{2}\theta &4\sin6\theta \\\sin^{2}\theta & \cos^{2}\theta &1+ 4\sin6\theta\end{bmatrix}=0\]
are given by
a) \[\pi/36, 5\pi/36\]
b) \[7\pi/36, 11\pi/36\]
c) \[5\pi/36, 7\pi/36\]
d) \[11\pi/36, \pi/36\]
Explanation: