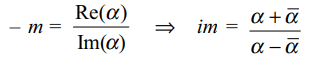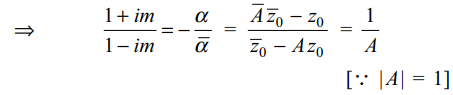PrepBharat

1. If \[f\left(z_{1},z_{2},z_{3}\right)=sgn \begin{bmatrix}1 &1&1 \\z_{1} &z_{2}&z_{3}\\\bar{z}_{1}& \bar{z}_{2} & \bar{z}_{3} \end{bmatrix}\]
, then for a \[\epsilon\] C,
a) \[f\left(z_{1},z_{2},z_{3}\right)=f\left(z_{1}+a,z_{2}+a,z_{3}+a\right)\]
b) \[f\left(z_{1},z_{2},z_{3}\right)=\mid a\mid f\left(z_{1},z_{2},z_{3}\right)\]
c) \[f\left(z_{1},z_{2},z_{3}\right)=\mid a\mid f\left(a_{1},a_{2},a_{3}\right)\]
d) none of these

View Answer

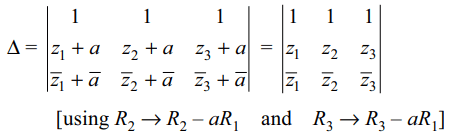
2.If \[z_{1},z_{2},z_{3}\]  are three complex numbers, then \[\mid z_{2}+z_{3}\mid^{2}+\mid z_{3}+z_{1}\mid^{2}+\mid z_{1}+z_{2}\mid^{2}\]       equal
a) \[2\mid z_{1}+z_{2}+z_{3}\mid^{2}\]
b) \[\mid z_{1}+z_{2}+z_{3}\mid^{2}\]
c) \[2\mid z_{1}+z_{2}+z_{3}\mid^{2}-\mid z_{1}\mid^{2}-\mid z_{2}\mid^{2}-\mid z_{3}\mid^{2}\]
d) none of these

View Answer

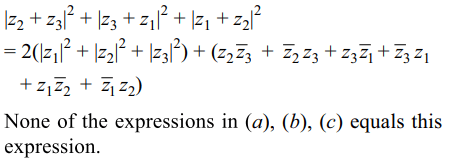
3. If \[\mid z\mid=1,\mid a\mid\neq 1\]   and \[x=z/\left( z-a \right)\left(1-z\bar{a}\right)\]    , then
a) x < 0
b) x > 0
c) \[x \geq 1\]
d) 0 < x < 1

View Answer

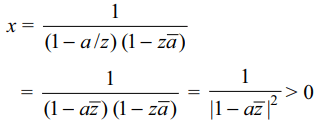
4. Let \[z_{1},z_{2}\epsilon C\]   and \[x= \mid z_{1}z_{2}\mid-Re \left(z_{1}z_{2}\right)-\frac{1}{2}\mid \bar{z}_{1}-z_{2}\mid^{2}+\frac{1}{2}\left(\mid z_{2}\mid-\mid z_{1}\mid\right)^{2}\]
a) x < 0
b) x= 0
c) \[x \geq 1\]
d) 0 < x < 1

View Answer

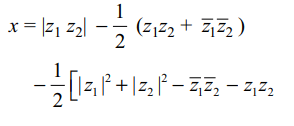
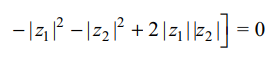
5. If the ratio\[\frac{1-z}{1+z}\]   is purely imaginary, then
a) \[|z| \leq 1/2\]
b) |z| = 1
c) |z| > 1
d) 0 < |z| < 1

View Answer

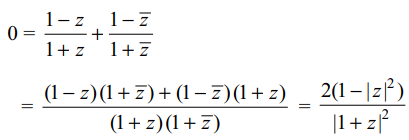
6. If \[\mid a\mid \neq\mid b\mid\]   , then the equation \[az+b\bar{z}+c=0\]     represents
a) a circle
b) an ellipse
c) a straight line
d) a point

View Answer

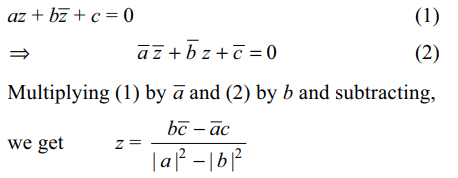
7. If \[\mid a\mid =\mid b\mid\]   and \[\bar{a}c \neq b\bar{c}\]   , then the equation \[az+b\bar{z}+c=0\]    has
a) no solution
b) exactly one solution
c) finitely many solutions
d) infinitely many solutions

View Answer

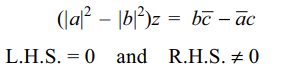
8. If \[\mid a\mid=\mid b\mid\neq 0\]   and \[\bar{a}c \neq b\bar{c}\]   , then \[az+b\bar{z}+c=0\]    represents
a) a circle
b) an ellipse
c) a straight line
d) a point

View Answer

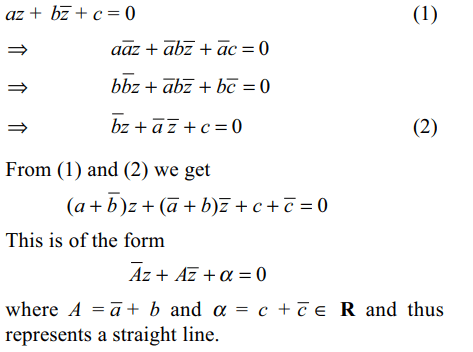
9.The equation \[\bar{z} =\bar{z}_{0}+A\left(z-z_{0}\right)\]    where A is a constant , represents
a) straight line
b) a circle
c) a point
d) none of these

View Answer

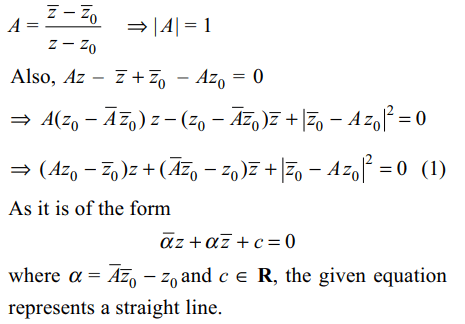
10.If m is slope of the straight line in above Question 9, then
a) \[A=\frac{1+im}{1-im}\]
b) \[A=\frac{1-im}{1+im}\]
c) \[A=\frac{i+m}{1-mi}\]
d) \[A=\frac{i-m}{1+mi}\]

View Answer