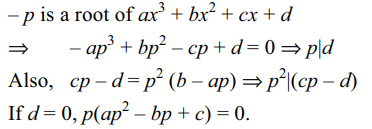1. Let P(x) be a polynomial such that
\[P \left(x+2 \right)=x^{2}+3x-2\] . Which one of the followings
are true statement?
a) Product of the roots of P(x) = 0 is – 4
b) P(x) must be of degree 2
c) P(x) = 0 has two irrational roots
d) All of the above
Explanation:
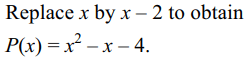
2. Let P(x) be a polynomial such that
\[P \left(x^{2}+2 \right)=x^{17}-3x^{5}+x^{3}-3\] , then
a) P(x) = 0 has at least 34 roots
b) P(x) = 0 has exactly 17 roots
c) Sum of the roots of P(x) = 0 is – 193
d) none of these
Explanation:
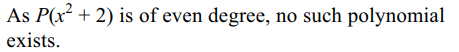
3. Let \[P \left(x \right)=a_{0}+a_{1}x+...+a_{n}x^{n},a_{n}\neq 0\] be such that
\[P \left(x^{2} \right)=P (x)^{2} \] , then
a) \[a_{0}=1\]
b) \[a_{0}=a_{1}=....=a_{n-1}=0\]
c) \[a_{n}=1\]
d) Both b and c
Explanation:

4. Let p, q be non-zero, real numbers and \[x_{1},x_{2},x_{3}\] be
the roots of \[x^{3}+px+q=0\] such that
\[x_{3}=\frac{1}{x_{1}}+\frac{1}{x_{2}}\] then
a) q is a root of \[x^{2}+px+q=0\]
b) q < 0
c) p < 0
d) Both a and c
Explanation:
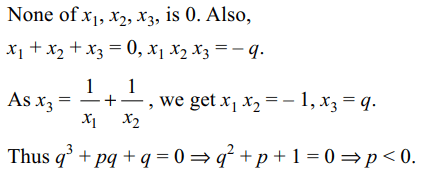
5. Let \[n\epsilon N, n>1\] and \[\alpha\epsilon R\] be such that sin\[\alpha \neq 0\] ,
and let \[p\left(x\right)=x^{n}\sin\alpha -x \sin n\alpha +
\sin \left(n-1\right) \alpha\]
then
a) \[\cos\alpha \pm 1\sin \alpha\] are zeros of p(x)
b) p(x) is divisible by \[x^{2}-2x \cos\alpha+1\]
c) p(x) is divisible by \[x^{2}+2x \cos\alpha+1\]
d) Both a and b
Explanation:
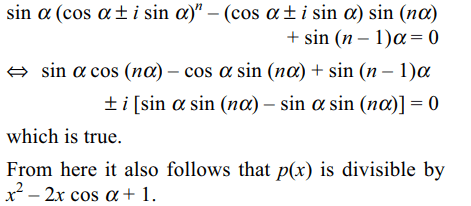
6. Let \[n \epsilon N, n>1\] and \[\alpha \epsilon R\] be such that \[\sin\alpha\neq 0\]
and let\[p\left(x\right)=\left(x\sin\alpha+\cos\alpha\right)^{n}-x\sin\left(n\alpha\right)-\cos\left(n\alpha\right)\]
then
a) \[\pm\] i are zeros of p(x)
b) p(x) is divisible by \[x^{2}+1\]
c) \[\pm\] 1 are zeros of p(x)
d) Both a and b
Explanation: p(x) is divisible by \[x^{2}+1\]
7. Let a, b, c > 0 and for all \[p,q \epsilon R\] with p + q = 1
\[pa^{2}+qb^{2}>pbc^{2}\] , then
a) a + b > c
b) a + c > b
c) b + c > a
d) All of the above
Explanation:
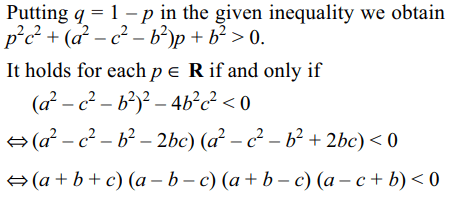
8. Let a, b be two distinct roots of
\[x^{4}+x^{3}-1=0\] , and p(x) = \[x^{6}+x^{4}+x^{3}-x^{2}-1\]
a) ab is a root of p(x) = 0
b) a + b is a root of p(x) = 0
c) both a + b and ab are roots of p(x) = 0
d) none of ab, a + b is a root of p(x) = 0
Explanation:
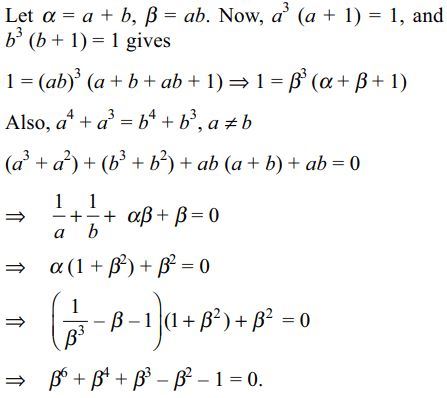
9. If \[x^{2}+px+1\] is a factor of \[ax^{3}+bx+c\] , then
a) ax + c is also a factor of \[ax^{3}+bx+c\]
b) ap+c=0
c) \[a^{2}-c^{2}=ab\]
d) All of the above
Explanation:
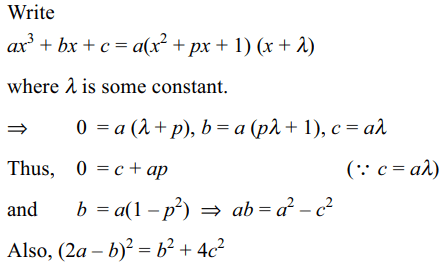
10. Let a, b, c, d and p be integers such that \[p\neq 0\] . If
x + p is a factor of \[ax^{3}+bx^{2}+cx+d\] , then
a) \[p\mid d\]
b) \[p^{2}\mid \left(pc-d \right)\]
c) \[d=0\Rightarrow p\] is a root of \[ax^{2}-bx+c=0\]
d) All of the above
Explanation: