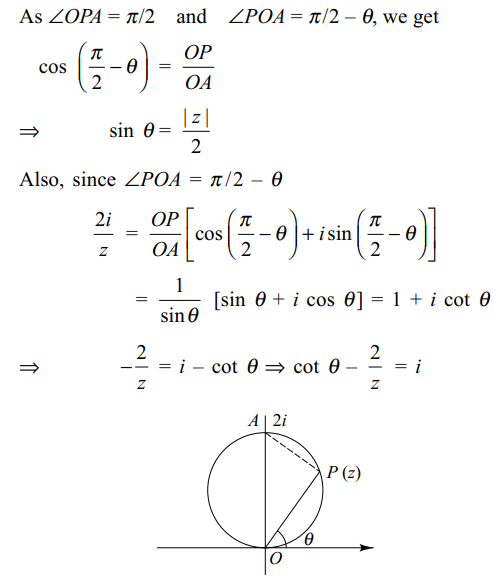1. If \[\mid z-25i\mid\leq 15\] , then
|maximum arg (z) – minimum arg (z)| equals
a) \[2\cos^{-1}\left(3/5\right)\]
b) \[2\cos^{-1}\left(4/5\right)\]
c) \[\pi/2+\cos^{-1}\left(3/5\right)\]
d) \[\sin^{-1}\left(3/5\right)-\cos^{-1}\left(3/5\right)\]
Explanation: If \[\mid z-25i\mid\leq 15\] ,then z lies either in the interior and or on the boundary of the circle with centre at C (25i) and radius equal to 15. From the Figure, it is clear that argument is least for point A and argument is greatest for point B.
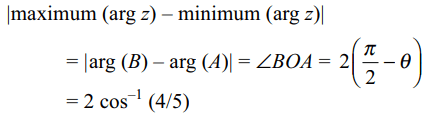
2. If \[\mid z_{1}\mid=\mid z_{2}\mid=\mid z_{3}\mid=1\] and \[z_{1}+z_{2}+z_{3}=0\] ,
then area of the triangle whose vertices are \[z_{1},z_{2},z_{3}\] is
a) \[3\sqrt{3}/4\]
b) \[\sqrt{3}/4\]
c) 1
d) 2
Explanation:
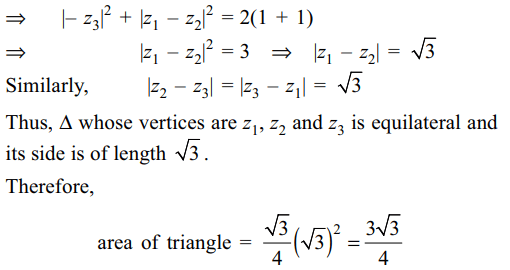
3. Shaded region is given by
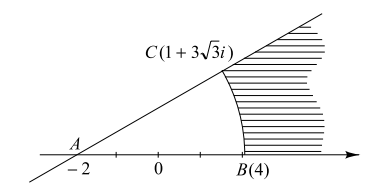
a) \[\mid z +2\mid\geq 6,0\leq arg \left(z\right)\leq\frac{\pi}{6}\]
b) \[\mid z+2\mid\geq 6,0\leq arg \left(z\right)\leq\frac{\pi}{3}\]
c) \[\mid z+2\mid\geq 6,0\leq arg \left(z\right)\leq\frac{\pi}{2}\]
d) none of these.
Explanation: Note that AB = 6 and
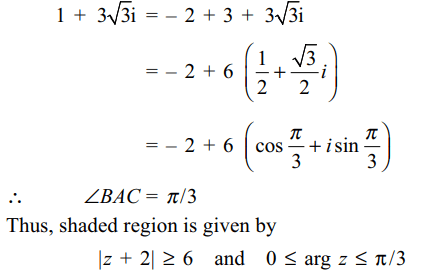
4. If \[-\pi < arg \left(z\right)< -\frac{\pi}{2}\] , then arg \[\bar{z}\] - arg \[(-\bar{z})\] is
a) \[\pi\]
b) \[-\pi\]
c) \[\frac{\pi}{2}\]
d) \[-\frac{\pi}{2}\]
Explanation: Let arg (z) = \[\theta\] , then arg \[\overline{z}\] = – \[\theta\] and arg (– \[\overline{z}\] ) = \[-\pi-\theta\]
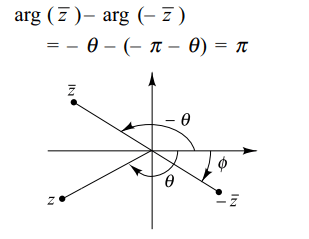
5. If \[k>1,\mid z_{1}\mid< k \] and \[\mid\frac{k- z_{1}\bar{ z_{2}}}{ z_{1}-k z_{2}}\mid=1\] , then
a) \[\mid z_{2}\mid< k\]
b) \[\mid z_{2}\mid= k\]
c) \[ z_{2}=0\]
d) \[\mid z_{2}\mid= 1\]
Explanation:
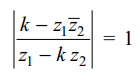
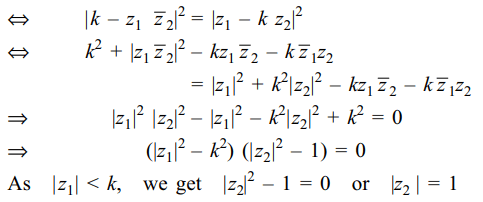
6. If \[k>0,\mid z\mid=\mid w\mid=k\] , and \[\alpha=\frac{z-\bar{w}}{k^{2}+z\bar{w}}\]
then Re \[\left(\alpha\right)\] equals
a) 0
b) k/2
c) k
d) 2k/3
Explanation:
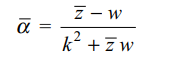
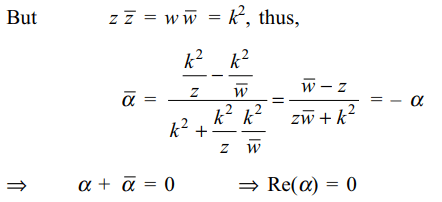
7. Roots of the equation are \[\left(z+1\right)^{5}=\left(z-1\right)^{5}\]
are
a) \[\pm i\tan\left(\frac{\pi}{5}\right),\pm i\tan\left(\frac{2\pi}{5}\right)\]
b) \[\pm i\cot\left(\frac{\pi}{5}\right),\pm i\cot\left(\frac{2\pi}{5}\right)\]
c) \[\pm i\cot\left(\frac{\pi}{5}\right),\pm i\tan\left(\frac{2\pi}{5}\right)\]
d) none of these
Explanation: For z \[\neq\] 1, (1) can be written as
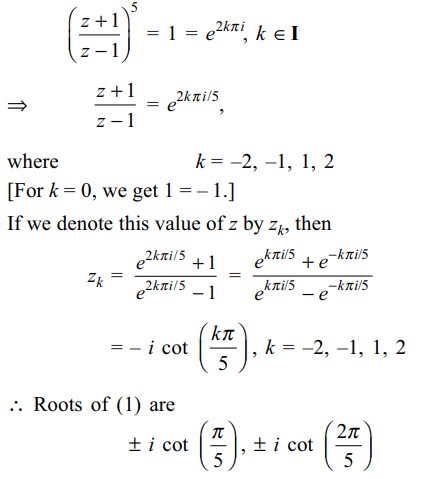
8. Let \[z_{1},z_{2},z_{3}\] be three distinct complex
numbers lying on a circle with centre at the origin such
that \[z_{1}+z_{2}z_{3} , z_{2}+z_{3}z_{1}\] and \[z_{3}+z_{1}z_{2}\] are real numbers, then
\[z_{1}z_{2}z_{3}\] equals
a) -1
b) 0
c) 1
d) i
Explanation: As z1, z2, z3 lie on a circle with centre at the origin,
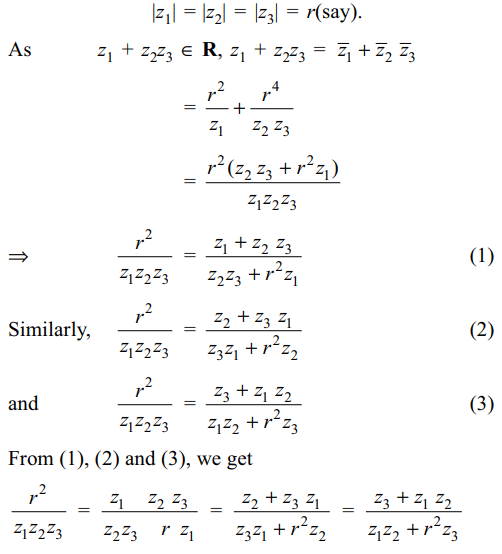
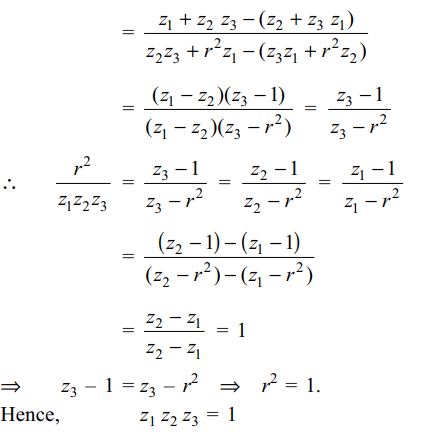
9. If the points z, – iz and 1 are collinear
then z lies on
a) a straight line
b) a circle
c) an ellipse
d) a pair of straight lines
Explanation: As z, – iz and 1 are collinear
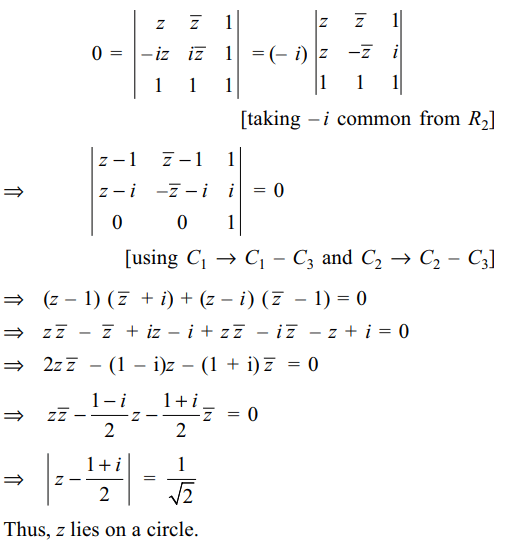
10. If \[\mid z-i\mid=1 \] and arg \[\left(z\right)=\theta \] where
\[\theta \epsilon \left(0 ,\pi/2\right)\] , then
\[\cot\theta-\frac{2}{z}\]
equals
a) 2i
b) -i
c) i
d) 1+i
Explanation: \[\mid z-i\mid=1 \] represents a circle with centre at i and radius 1. As 0 < \[\theta\] < \[\pi\]/2, \[\theta\] lies on the semi-circle in the first quadrant.