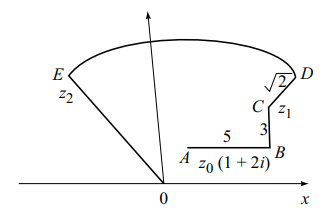
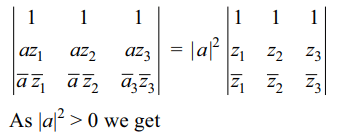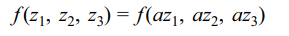1. A particle P starts from the point \[z_{0}=1+2i\] ,
where \[i=\sqrt{-1}\] . It moves first horizontally away from the
origin by 5 units and then vertically away from the origin
by 3 units to reach a point \[z_{1}\] . From \[z_{1}\] the particle moves
\[\sqrt{2}\] units in the direction of \[\hat{i}+\hat{j}\] and then it moves through
an angle \[\pi/2\] in the anticlockwise direction on a circle with
centre at origin, to reach point \[z_{2}\]. The point \[z_{2}\] is given by
a) 6+7i
b) -7+6i
c) 7+6i
d) -6+7i
Explanation:
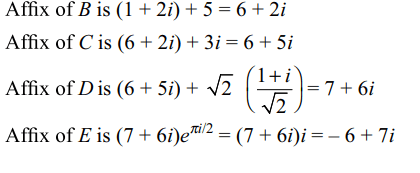
2. If P( \[\omega\] ) lies on the chord joining A, B
where A(a), B(b) lie on the unit circle |z| = 1, then \[\bar{\omega}\]
is equal to
a) \[\frac{a+b-\omega}{a+b}\]
b) \[\frac{a+b-\omega}{ab}\]
c) \[\frac{1}{2}\left(a+b\right)-\frac{\omega}{ab}\]
d) \[\frac{1}{ab}\left(a+b+\omega\right)\]
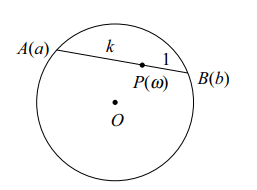
Explanation: Suppose P( \[\omega\] ) divides the join of A, B in the ratio k : 1, then
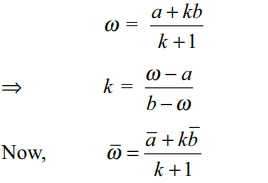
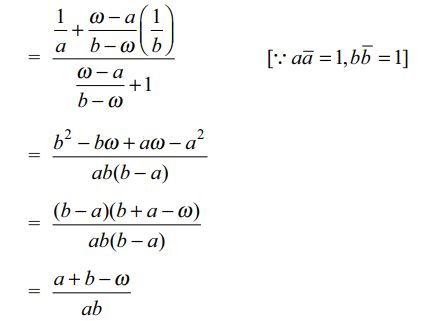
3. Number of solution of
\[\mid z-7-i\mid=3\sqrt{2}\] (1)
and \[\mid z-1-7i\mid\leq3\sqrt{2}\] (2)
is
a) 0
b) 1
c) 2
d) 3
Explanation: \[\mid z-7-i\mid=3\sqrt{2}\] represents a circle C1 with centre at A(7 + i) and radius r1 = \[3\sqrt{2}\]
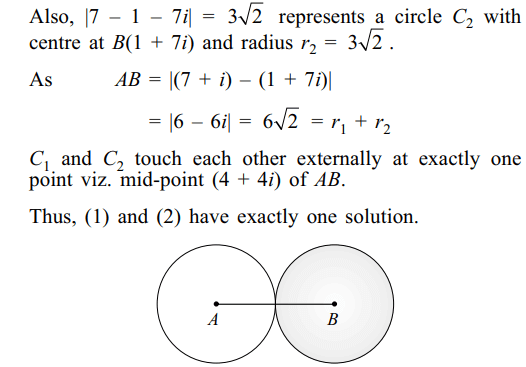
4. Let \[z=\begin{bmatrix}7+5i & 3+3i \\8+5i & 5+2i \end{bmatrix}\]
then det \[\left(Z\bar{Z}\right)\] , (where \[\bar{Z}\] is the matrix obtained by taking
Z) is equal to
a) 256
b) 121
c) 36
d) 25
Explanation:
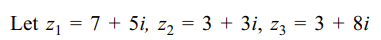
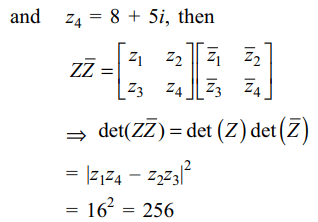
5. Let a, b, c be three points lying on the
circle \[\mid z\mid=1\] and suppose \[\alpha \epsilon\left(0,\pi/2\right)\] be such that \[a+b\cos\alpha+c\sin\alpha=0\] , then
a) \[b=\pm ic\]
b) \[2a^{2}+b^{2}+c^{2}=0\]
c) \[a^{2}+b^{2}+c^{2}=0\]
d) b=c
Explanation:
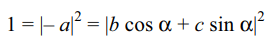
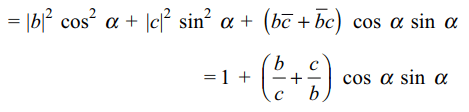
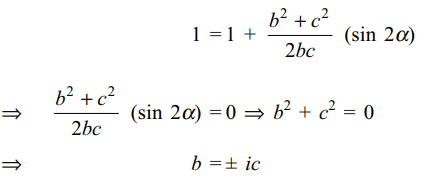
6. Let \[x_{1},x_{2},x_{3},x_{4}\epsilon C\] be such that
\[x_{1}\left(x_{1}-x_{2}\right)\left(x_{1}-x_{3}\right)\left(x_{1}-x_{4}\right)=4\]
\[x_{2}\left(x_{2}-x_{1}\right)\left(x_{2}-x_{3}\right)\left(x_{2}-x_{4}\right)=4\]
\[x_{3}\left(x_{3}-x_{1}\right)\left(x_{3}-x_{2}\right)\left(x_{3}-x_{4}\right)=4\]
\[x_{4}\left(x_{4}-x_{1}\right)\left(x_{4}-x_{2}\right)\left(x_{4}-x_{3}\right)=4\]
a) \[x_{1}+x_{2}+x_{3}+x_{4}=0\]
b) \[x_{1}x_{2}x_{3}x_{4}=-1\]
c) \[x_1^2+x_2^2+x_3^2+x_4^2=0\]
d) All of the Above
Explanation: Note that none of xi is zero and no two of xi’s are equal.
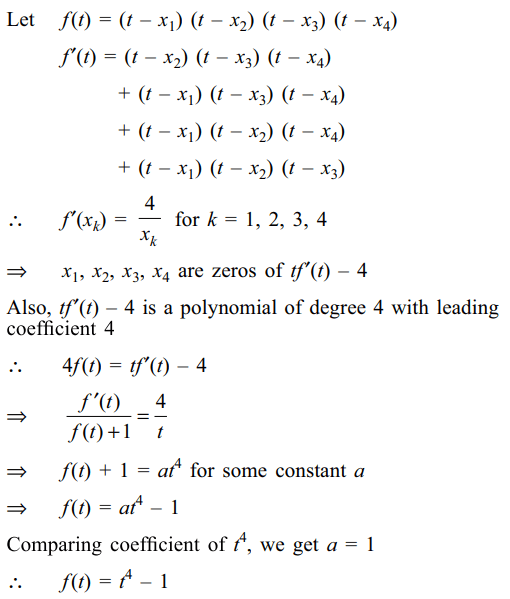
7. Let \[z_{1},z_{2}\] be two non-zero complex numbers such
that \[\left(\mid z_{1}\mid-\mid z_{2}\mid\right)^{2}+ \mid z_{1}z_{2}\mid=\bar{z}_{1}z_{2}+z_{1}\bar{z}_{2}\]
then
\[\mid\frac{z_{2}}{z_{1}}\mid\] lies in the interval
a) \[\left[\frac{1}{2}\left(3-\sqrt{5}\right),\frac{1}{2}\left(3+\sqrt{5}\right)\right]\]
b) \[\left[\frac{1}{2}\left(\sqrt{5}-1\right),\frac{1}{2}\left(\sqrt{5}+1\right)\right]\]
c) \[\left[1,\frac{1}{2}\left(3+\sqrt{5}\right)\right]\]
d) \[\left[\frac{1}{2}\left(3-\sqrt{5}\right),1\right]\]
Explanation:
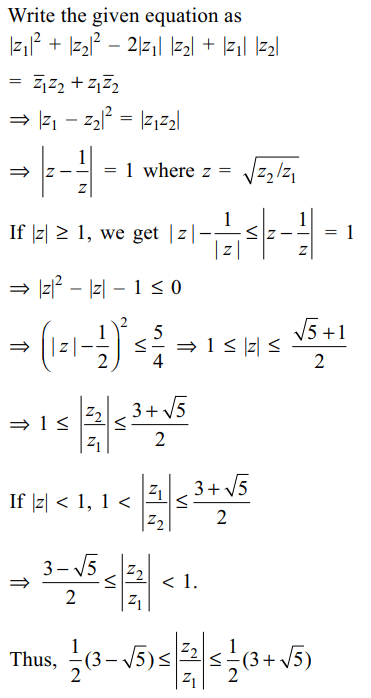
8. Suppose A(a), B(b) lie on the unit circle |z| = 1. If \[\omega\]
is a complex number such that\[\bar{\omega}=\frac{b+a-\omega}{ab}\] , then
\[P\left(\omega\right)\] lies on
a) chord AB
b) perpendicular bisector of chord AB
c) unit circle |z| = 1
d) the circle |z| = 1/2
Explanation:
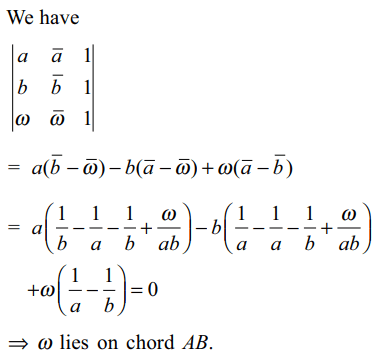
9. If \[\mid z_{1}\mid\neq1\] , \[\mid\frac{z_{1}-z_{2}}{1-\bar{z}_{1}z_{2}}\mid=1\] , then
a) \[\mid z_{2}\mid=1\]
b) \[\mid z_{2}\mid=0\]
c) \[\mid z_{2}\mid>1\]
d) \[0<\mid z_{2}\mid<1\]
Explanation:
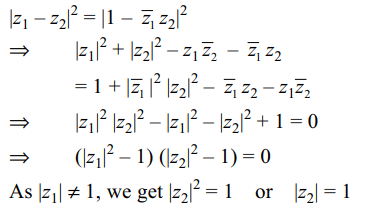
10. Let \[z_{1}, z_{2}, z_{3}\epsilon C\]
\[f\left(z_{1},z_{2},z_{3}\right)=sgn \begin{bmatrix}1 &1&1 \\z_{1} &z_{2}&z_{3}\\\bar{z}_{1}& \bar{z}_{2} & \bar{z}_{3} \end{bmatrix}\]
where sgn x = \[\frac{x}{\mid x\mid} \] if \[x\neq 0\] and sgn(0)=0, then for \[a\neq 0\]
a) \[f\left(z_{1},z_{2},z_{3}\right)=f\left(az_{1},az_{2},az_{3}\right)\]
b) \[f\left(z_{1},z_{2},z_{3}\right)=f\left(az_{2},az_{1},az_{3}\right)\]
c) \[f\left(z_{1},z_{2},z_{3}\right)=f\left(az_{3},az_{2},az_{1}\right)\]
d) none of these
Explanation: