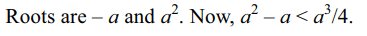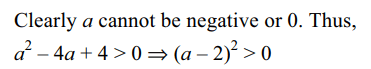1. The number of irrational roots of the equation
\[\frac{4x}{x^{2}+x+3}+\frac{5x}{x^{2}+5x+3}=-\frac{3}{2}\]
is
a) 0
b) 1
c) 2
d) 3
Explanation:
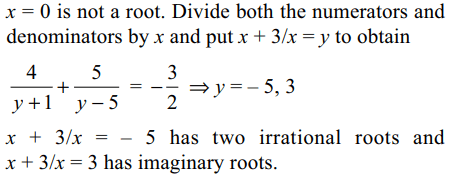
2. If \[\alpha,\beta,\gamma,\delta\] are the roots of
\[\left(x^{2}+x+4\right)^{2}+3x\left(x^{2}+x+4\right)+2x^{2}=0\]
then \[\mid\alpha\mid+\mid\beta\mid+\mid\gamma\mid+\mid\delta\mid\] is equal
a) 6
b) 8
c) 12
d) 25
Explanation:
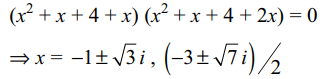
3. x = 1 is a root of
\[\left(x^{2}-x+1\right)^{4}-6x^{2}\left(x^{2}-x+1\right)^{2}+5x^{4}=0\]
of multiplicity
a) 2
b) 3
c) 4
d) 6
Explanation:
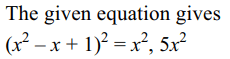
4. The number of irrational roots of the equation
\[\left(x^{2}-3x+1\right)\left(x^{2}+3x+2\right)\left(x^{2}-9x+20\right)=-30\]
is
a) 0
b) 2
c) 4
d) 6
Explanation:
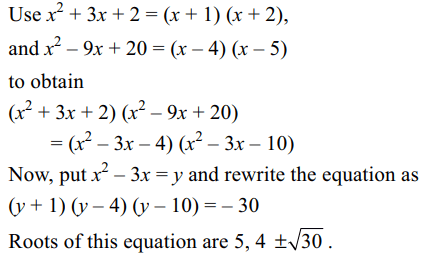
5.The number of roots of the equation
\[\sqrt{3x^{2}+6x+7}+\sqrt{5x^{2}+10x+14}=4-2x-x^{2}\]
is
a) 4
b) 3
c) 2
d) 1
Explanation:
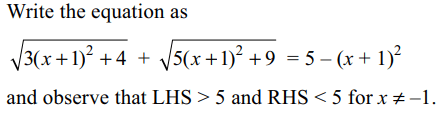
6. The number of real values of x which satisfy the
equation \[\mid\frac{x^{2}-6\sqrt{x}+7}{x^{2}+6\sqrt{x}+7}\mid=1\]
a) 0
b) 1
c) 2
d) infinite
Explanation:
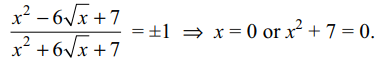
7. The number of real values of x which satisfy the
equation \[\mid\frac{x}{x-1}\mid+\mid x\mid =\frac{x^{2}}{\mid x-1\mid}\]
a) 1
b) 2
c) 5
d) infinite
Explanation:
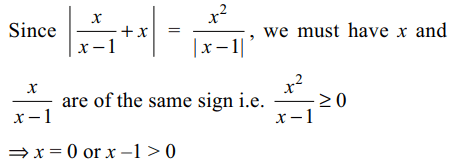
8. Sum of all the real values of x which satisfy the
equation \[\frac{\sqrt{2-x}}{\sqrt{2+x}}=\frac{2-x}{2+x}\]
a) 0
b) 2
c) 7.5
d) 11.5
Explanation:
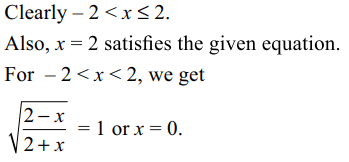
9. The set of real values of a for which the equation
\[\frac{2a^{2}+x^{2}}{a^{3}-x^{3}}-\frac{2x}{ax+a^{2}+x^{2}}+\frac{1}{x-a}=0\]
has a unique solution is
a) \[\left(-\infty,1\right)\]
b) \[\left(-1,\infty\right)\]
c) \[\left(-1,1\right)\]
d) \[R-\left\{0\right\}\]
Explanation:
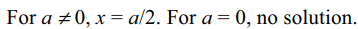
10. The set of real values of a for which sum of the
roots of the equation\[\frac{1}{x}+\frac{1}{a}-\frac{1}{a^{2}}=\frac{1}{x+a-a^{2}}\]
is less than \[a^{3}/4\] is
a) \[\left(0,2\right)\cup\left(2,\infty\right)\]
b) \[\left(3,\infty\right)\]
c) \[\left(-1,0\right)\cup\left(3,\infty\right)\]
d) \[\left(2,\infty\right)\]
Explanation: