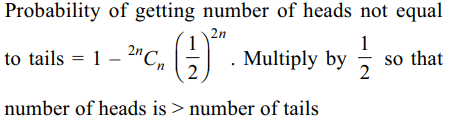1. Two non-negative integers are chosen at random.
The probability that the sum of the square is
divisible by 11 is
a) 9/16
b) 1/121
c) 9/17
d) 2/121
Explanation:
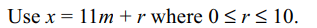
2. A natural number x is choosen at random from the
first 100 natural numbers. The probability that
\[x+\frac{100}{x}>50\]
is
a) 1/10
b) 11/50
c) 11/20
d) 3/20
Explanation:
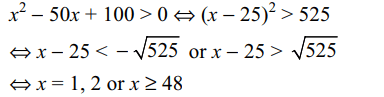
3. A bag contains (2n + 1) coins. It is known that
n of these coins have a head on both sides, whereas
the remaining (n + 1) coins are fair. A coin is
picked up at random from the bag and tossed. If the probability that the toss results in a head is 31/42,
then n is equal to
a) 10
b) 11
c) 12
d) 13
Explanation:

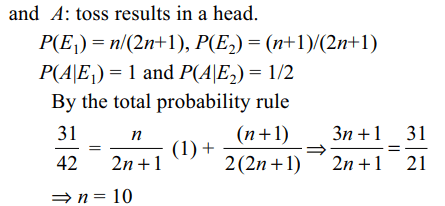
4. If X and Y are independent binomial variate
B (5, 1/2) and B (7, 1/2), then P (X + Y = 3) is
a) 55/1024
b) 55/4098
c) 55/2048
d) 55/512
Explanation:
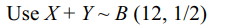
5. Suppose \[n\left(\geq 3\right)\] persons are sitting in a row. Two of
them are selected at random. The probability that
they are not together is
a) \[1-\frac{2}{n}\]
b) \[\frac{2}{n-1}\]
c) \[1-\frac{1}{n}\]
d) \[\frac{2}{n}\]
Explanation:
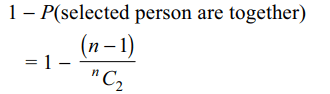
6. A bag contains four tickets marked with numbers
112, 121, 211, 222. One ticket is drawn at random
from the bag. Let \[E_{i}\left(i=1,2,3\right)\] denote the event
that ith digit on the ticket is 2. Then which of the
following is not true
a) \[E_{1}\] and \[E_{2}\] are independent
b) \[E_{2}\] and \[E_{3}\]are independent
c) \[E_{3}\] and \[E_{1}\] are independent
d) \[E_{1},E_{2}, E_{3}\] are independent
Explanation:
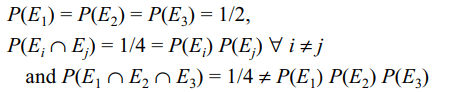
7. If the letters of the word PROBABILITY are
written down at random in a row, the probability
that two B's are together is
a) 2/11
b) 10/11
c) 3/11
d) 6/11
Explanation:
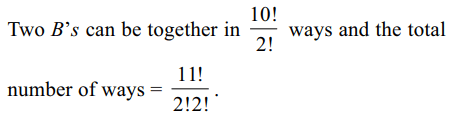
8. If four positive integers are taken at random and
multiplied together, then the probability that the
last digit is 1, 3, 7 or 9 is
a) 1/8
b) 2/7
c) 1/625
d) 16/625
Explanation:

9. Two contestants play a game as follows: each is
asked to select a digit from 1 to 9. If the two digits
match they both win a prize. The probability that
they will win a prize in a single trial is
a) 1/8
b) 7/81
c) 1/9
d) 3/11
Explanation: Total number of ways is 81 out of which 9 are favourable
10. A fair coin is tossed 2n times. Probability of getting
more heads than tails is
a) 1/2
b) \[^{2n}C_{n}\left(\frac{1}{2}\right)^{2n}\]
c) \[1-2^{n}C_{n}\left(\frac{1}{2}\right)^{2n}\]
d) \[\frac{1}{2}-^{2n}C_{n}\left(\frac{1}{2}\right)^{2n+1}\]
Explanation: