1. Each of two persons A and B toss three
fair coins. The probability that both get the same number
of heads is
a) \[\frac{3}{8}\]
b) \[\frac{1}{9}\]
c) \[\frac{5}{16}\]
d) \[\frac{7}{16}\]
Explanation: Let X be the number of heads obtained by A and Y be the number of heads obtained by B. Note that both X and Y are binomial variate with parameters n = 3 and p = 1/2.
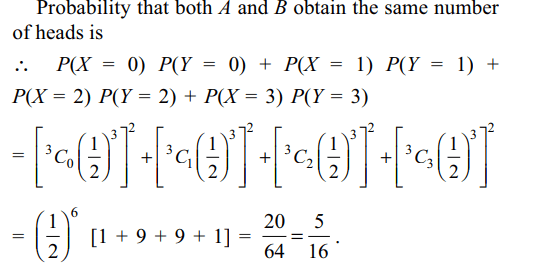
2. Three boys and two girls stand in a
queue. The probability, that the number of boys ahead of
every girl is at least one more than the number of girls
ahead of her, is
a) \[\frac{1}{2}\]
b) \[\frac{1}{3}\]
c) \[\frac{2}{3}\]
d) \[\frac{3}{4}\]
Explanation: Let E denote the event that the number of boys ahead of every girl is at least one more than the number of girls ahead of her. Note that E' consists of the following arrangements.
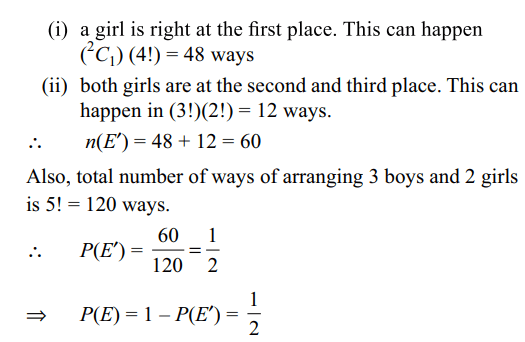
3. Six distinct numbers are selected from
first 150 natural number. The probability all the six
numbers are divisible both by 3 and 5 is
a) 1/33
b) 1/35
c) 1/49
d) none of these
Explanation: Total number of ways of selecting 6 numbers
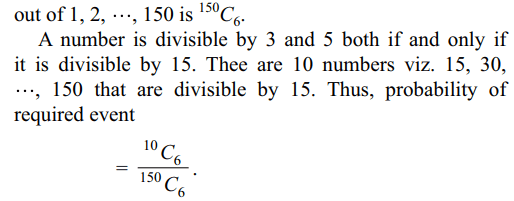
4. There are two balls in an urn whose
colours are not known (each ball can be either white or
black). A white ball is put into the urn. A ball is drawn from
the urn. The probability that it is white is
a) 1/4
b) 1/3
c) 2/3
d) 1/6
Explanation:


5. A natural number x is chosen at random from the first one hundred natural numbers. The probability that \[\frac{\left(x-20\right)\left(x-40\right)}{x-30} < 0\]
is
a) 1/50
b) 3/50
c) 3/25
d) 7/25
Explanation:
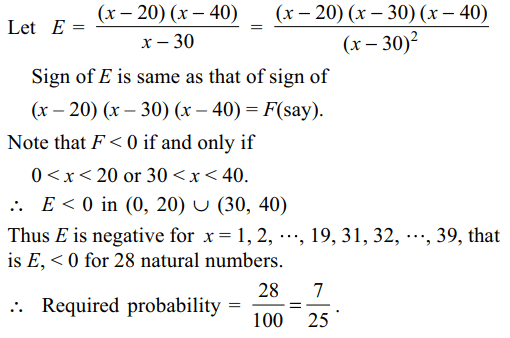
6. An experiment has 10 equally likely
outcomes. Let A and B be two non-empty events of the
experiment. If A consists of 4 outcomes, the number
of outcomes that B must have so that A and B are
independent, is
a) 2, 4 or 8
b) 3, 6 or 9
c) 4 or 8
d) 5 or 10.
Explanation:

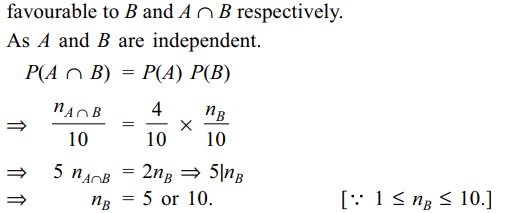
7. If A, B and C are three events such that
\[P\left(B\right)=\frac{3}{4},P\left(A\cap B\cap C' \right)=\frac{1}{3}\]
and \[P\left(A'\cap B\cap C' \right)=\frac{1}{3}\] ,
then \[P\left( B\cap C \right)\] is equal to
a) \[\frac{1}{12}\]
b) \[\frac{1}{6}\]
c) \[\frac{1}{15}\]
d) \[\frac{1}{9}\]
Explanation:
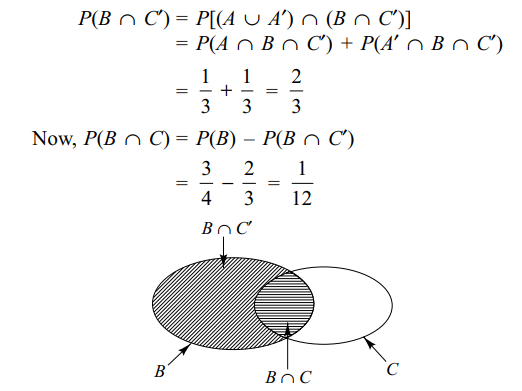
8. A fair coin is tossed n times. If the
probability that head occurs 6 times is equal to the
probability that head occurs 8 times, then value of n is
a) 24
b) 48
c) 14
d) 16
Explanation: Let X be the number of times head occurs.

9. A person writes 4 letters and 4 addresses
on 4 envelopes. If the letters are placed in the envelopes
at random, the probability that not all letters are placed in
correct envelopes is
a) 1/24
b) 11/24
c) 5/8
d) 23/24
Explanation: Required probability
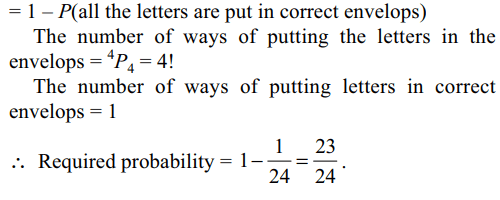
10. A letter is known to have come from either
TATANAGAR or CALCUTTA .on the envelope , just two
consecutive letters, TA, are visible. The probability that
the letter has come from CALCUTTA is
a) 4/11
b) 1/3
c) 5/12
d) 1/7
Explanation: Let E1 denote the event that the letter came
