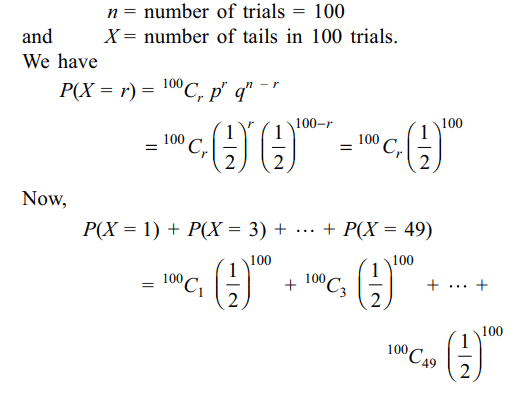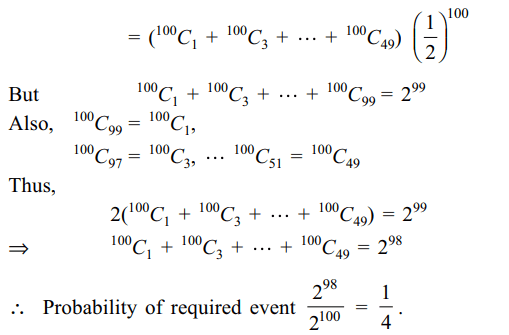1. A computer producing factory has only
two plants \[T_{1}\] and \[T_{2}\] . Plant \[T_{1} \] produces 20% and plant
\[T_{2} \] produces 80% of the total computers produced. 7% of
computers produced in the factory turn out of be defective.
It is known that
P(computer turns out to be defective given that it is
produced in plant \[T_{1} \])
= 10 P (computer turns out to be defective given that it is
produced in plant \[T_{2} \])
where P(E) denotes the probability of an event E. A
computer produced in the factory is randomly selected and
it does not turn out to be defective. Then the probability
that it is produced in plant \[T_{2} \] is
a) \[\frac{36}{73}\]
b) \[\frac{47}{79}\]
c) \[\frac{78}{93}\]
d) \[\frac{75}{83}\]
Explanation: Let T1, T2, D denote the following events.

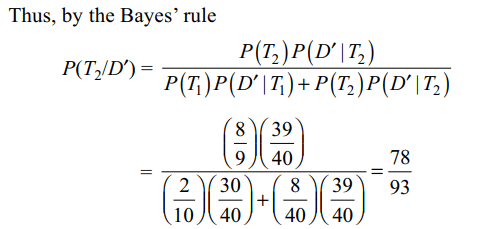
2. Seven distinct white balls and three distinct
black balls are randomly placed in a row. The probability
that no two black balls are placed adjacently equals
a) 1/2
b) 7/15
c) 2/15
d) 1/3
Explanation: The number of ways of placing 3 black balls at
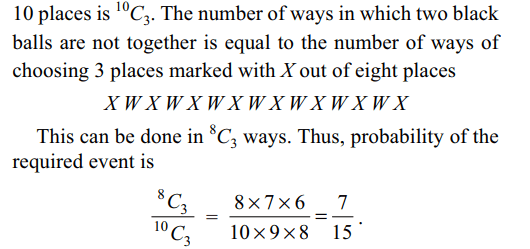
3. If from each of the three boxes containing
3 white and 1 black, 2 white and 2 black, 1 white and
3 black balls, one ball is drawn at random, then the
probability that two white and one black ball will be
drawn is
a) \[\frac{13}{32}\]
b) \[\frac{1}{4}\]
c) \[\frac{1}{32}\]
d) \[\frac{3}{16}\]
Explanation: P (2 white and 1 black)
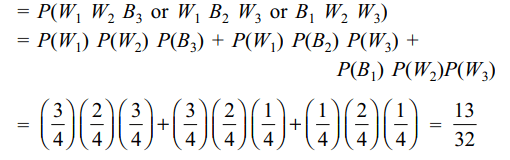
4. There are four machines and it is known
that exactly two of them are faulty. They are tested, one
by one, in a random order till both the faulty machines
are identified , then the probability that only two tests are
needed is
a) \[\frac{1}{3}\]
b) \[\frac{1}{6}\]
c) \[\frac{1}{2}\]
d) \[\frac{1}{4}\]
Explanation: Let A(B) denote the event that each of the first
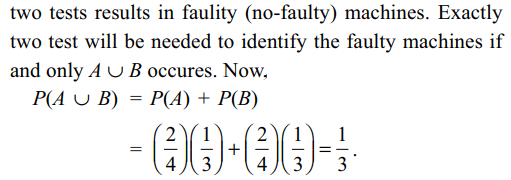
5. A bag contains some white and some
black balls, all combinations of balls being equally likely.
The total number of balls in the bag is 10. If three balls are
drawn at random without replacement and all of them are
found to be black, the probability that the bag contains 1
white and 9 black balls is
a) \[\frac{14}{55}\]
b) \[\frac{12}{55}\]
c) \[\frac{2}{11}\]
d) \[\frac{8}{55}\]
Explanation: Let Ei denote the event that the bag contains i
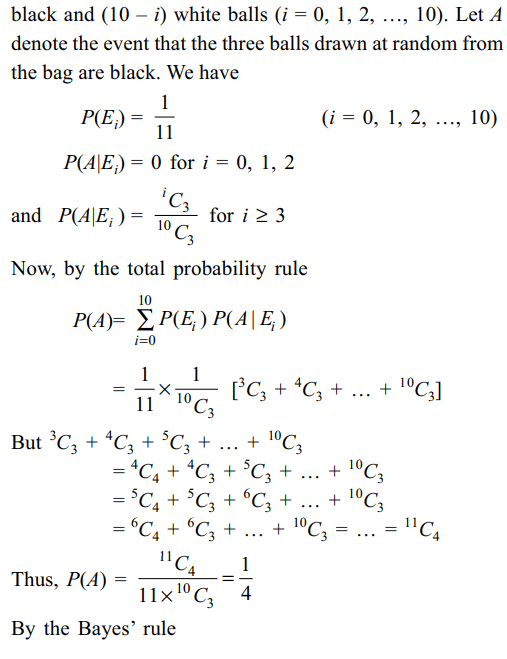
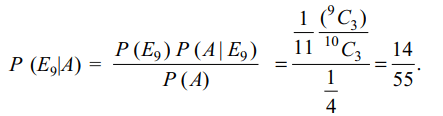
6. A group of 2n boys and 2n girls is
randomly divided into two equal groups. The probability
that each group contains the same number of boys and
girls is
a) 1/2
b) 1/n
c) \[\frac{^{2n}C_{n}}{^{4n}C_{n}}\]
d) \[\frac{\left(^{2n}C_{n}\right)^{2}}{^{4n}C_{n}}\]
Explanation: Total number of ways of choosing a group is
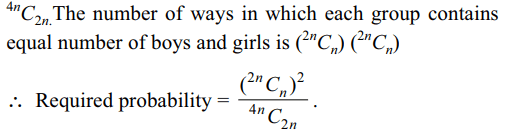
7. An unbiased die with faces marked 1,
2, 3, 4, 5 and 6 is rolled four times out of the four faces
obtained, the probability that the minimum value is exactly
than 2 and the maximum value is exactly 5 is
a) 4/27
b) 1/81
c) 80/81
d) 65/81
Explanation: Total number of outcomes of 4 dice is 64. We

8. Four fair dice \[D_{1},D_{2},D_{3}\] and \[D_{4}\] , each
having six faces numbered 1, 2, 3, 4, 5 and 6 are rolled
simultaneously. The probability that \[D_{4}\] shows a number
appearing on one of \[D_{1},D_{2},\] and \[D_{3}\] is
a) \[\frac{91}{216}\]
b) \[\frac{108}{216}\]
c) \[\frac{125}{216}\]
d) \[\frac{127}{216}\]
Explanation: Probability of the required event
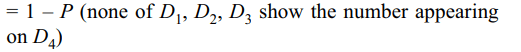
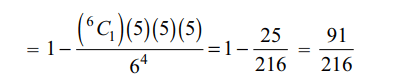
9. A pair of unbiased dice is rolled together
till a sum of either 5 or 7 is obtained. The probability that
5 comes before 7 is
a) 2/5
b) 3/5
c) 4/5
d) 1/5
Explanation: Let A denote the event that a sum of 5 occurs, B the event that a sum of 7 occurs and C the event that neither a sum of 5 nor a sum of 7 occurs. We have
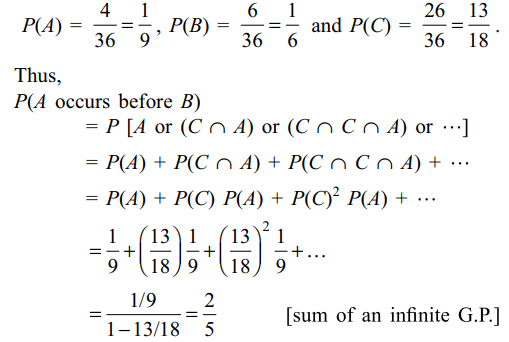
10. A fair coin is tossed 100 times. The
probability of getting tails 1, 3, .... , 49 times is
a) 1/2
b) 1/4
c) 1/8
d) 1/16
Explanation: Let p = probability of getting a tail in a single trial = 1/2