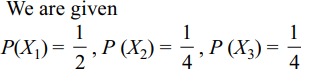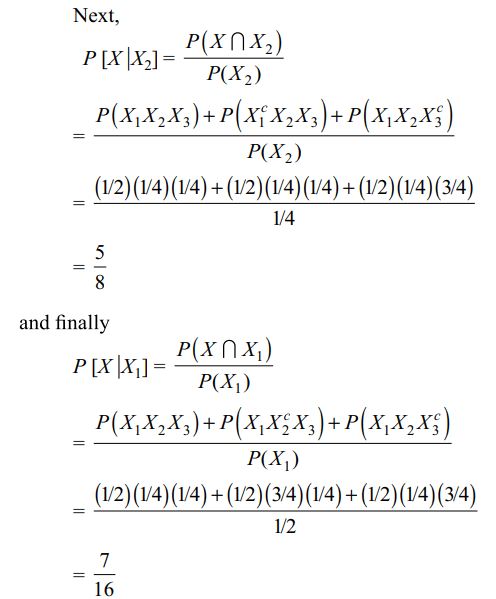1. For two events A and B, if
P(A) = P(A | B) = 1/4 and P(B | A) = 1/2, then
a) A and B are independent
b) P (A' | B) = 3/4
c) P (B' | A') = 1/2.
d) All of the Above
Explanation:
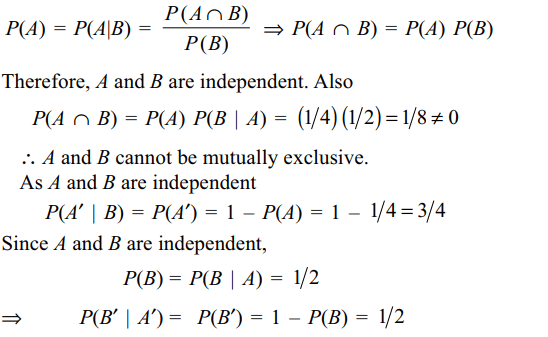
2. If A and B are two independent events
such that \[P\left(A' \cap B\right)=2/15\] and \[P\left(A \cap B'\right)=1/6\] , then
P(B) is
a) 1/5
b) 1/6
c) 4/5
d) Both b and c
Explanation: Since A and B are independent
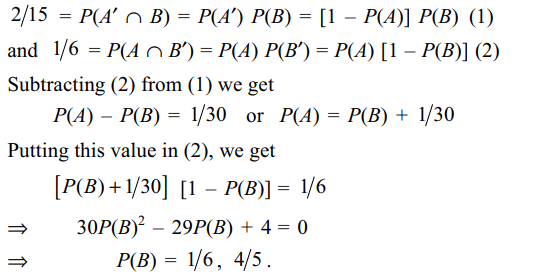
3. A student appears for tests I, II, and III.
The student is successful if he passes either in tests I
and II or tests I and III. The probabilities of the student
passing in tests I, II, III are p, q and 1 2, respectively. If
the probability that the student is successful is 1/2, then
a) p = 1, q = 0
b) p = 2/3, q = 1/2
c) p = 3/5, q = 2/3
d) All of the Above
Explanation: Let A, B and C be the events that the student is successful in tests I, II and III, respectively. Then
P(the student is successful)
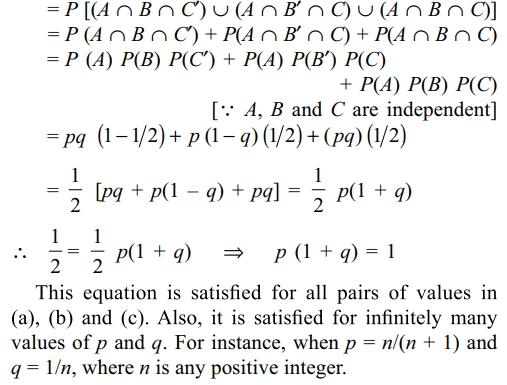
4. Let X be a set containing n elements. If two
subsets A and B of X are picked at random, the probability
that A and B have the same number of elements is
a) \[\frac{^{2n}C_{n}}{2^{2n}}\]
b) \[\frac{1}{^{2n}C_{n}}\]
c) \[\frac{1.3.5...\left(2n-1\right)}{2^{n}.\left(n !\right)}\]
d) Both a and c
Explanation: We know that the number of subsets of a set

5. Let E and F be two independent events.
The probability that both E and F happen is 1/12 and the
probability that neither E nor F happens is 1/2. Then
a) P(E) = 1/3, P(F) = 1/4
b) P(E) = 1/2, P(F) = 1/6
c) P(E) = 1/4, P(F) = 1/3
d) Both a and c
Explanation:
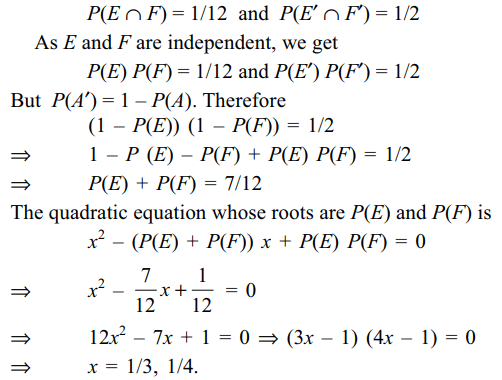
6. A random variable X follows binomial
distribution with mean a and variance b. Then
a) a > b > 0
b) \[\frac{a}{b}>1\]
c) \[\frac{a^{2}}{a-b}\] is an integer
d) All of the Above
Explanation: Suppose X ~ B(n, p). Then
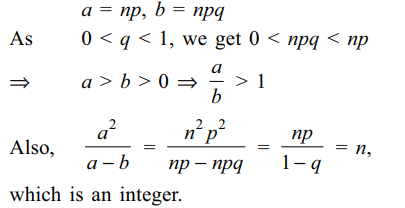
7. If A1,A2,....,An are n independent events
such that \[P\left(A_{i}\right)=\frac{1}{i+1},i=1,2,....,n\] . The probability that
none of A1,A2,....,An occurs is
a) \[\frac{n}{n+1}\]
b) \[\frac{1}{n+1}\]
c) less than \[\frac{1}{n}\]
d) Both b and c
Explanation:
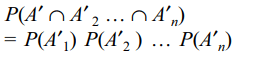

8. A four digit number (numbered from 0000to 9999) is said to be lucky if the sum of first two
digits is equal to the sum of its last two digits. If a four
digit number is picked up at random, then the probability
that it is lucky is
a) > 0.065
b) < 0.068
c) 0.067
d) All of the Above
Explanation: The total number of ways of choosing the ticket is 1000.
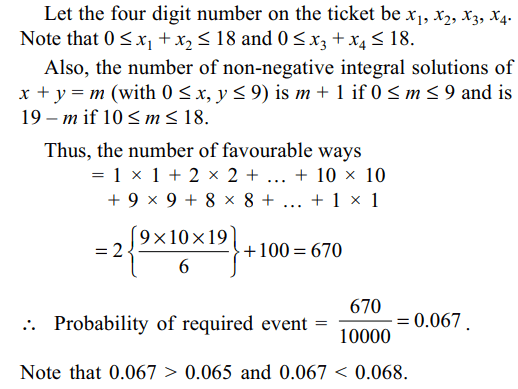
9. A bag contains n \[\left(\geq 7\right)\] balls number 1, 2, …
n. Four balls are taken out at random without replacement.
Let pn denote the probability that all the four balls bear odd
numbers, then
a) \[P_{n}=\frac{\left(n+1\right)\left(n-5\right)}{16n\left(n-3\right)}\] if n is odd
b) \[P_{n}=\frac{\left(n-4\right)\left(n-6\right)}{16n\left(n-1\right)\left(n-3\right)}a\] if n is even
c) \[P_{20}<\frac{7}{23}\]
d) All of the Above
Explanation: Let n = 2k + 1, k ≥ 3

10. A ship is fitted with three engines \[E_{1},E_{2}\] and \[E_{3}\]. The engines function independently of each other
with respective probabilities
\[\frac{1}{2},\frac{1}{4}\] and \[\frac{1}{4}\] For the ship to
be operational at least two of its engines must function. Let
X denote the event that the ship is operational and let \[X_{1},X_{2}\] and \[X_{3}\] denote respectively the events that the engines
\[E_{1},E_{2}\] and \[E_{3}\] are functioning. Which of the following is
(are) true?
a) \[P\left[X_1^c \mid X\right]=\frac{3}{16}\]
b) P [Exactly two engines of the ship are functioning | X] = \[\frac{7}{8}\]
c) \[P\left[X \mid X_{1}\right]=\frac{7}{16}\]
d) Both b and c
Explanation: