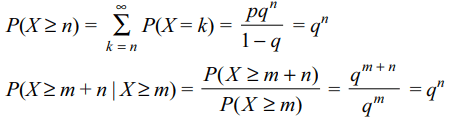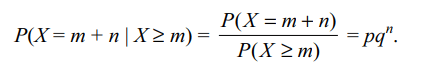1. If A and B are two events, then
a) \[P\left(A \cap B\right)\leq \min \left\{P\left(A\right), P\left(B\right)\right\}\]
b) \[P\left(A \cap B\right)\cap \max \left\{0,1-P\left(A'\right)- P\left(B'\right)\right\}\]
c) \[P\left(A \cap B\right)\leq P\left(A \cup B\right)\]
d) All of the Above
Explanation: All of the Above
2. Twenty children are standing in a line outside a
ticket window a appu ghar in New Delhi. Ten of
these children have a one-rupee coin each and the
remaining 10 have a two rupee coin each. The entry
ticket is priced at Re. 1. If all the arrange-ments of
the 20 children are equally likely, the probability that
the 10th chid will be the first to wiat for change is
(assume that cashier has no change to begin with.)
a) 0
b) < 1/2
c) >1/2
d) Both a and b
Explanation: The child standing at the even numbered place cannot be the first child to face the problem of change
3. Eight tickets numbered 000, 010, 011, 011, 100,
101, 101 and 110 are placed in a bag. One ticket
is drawn from the bag at random. Let A, B and C
denote the following events: A-" the first digit is
0”, B—“the second digit is 0” and C— “the third
digit is 0”. Then
a) A and B are independent
b) B and C are independent
c) C and A are independent
d) A, B, C are independent
Explanation:
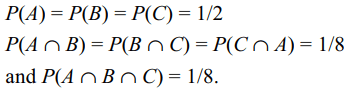
4. Four natural numbers are taken at random and are
multiplied. Let \[P_{1}\] denote the probability of the
event that last digit of the product is 1, 3, 7 or 9,
and \[P_{2}\] denote the probability that the last digit of
the product is 5, then
a) \[P_{1}> P_{2}\]
b) \[P_{1}< P_{2}\]
c) \[P_{1}+ P_{2}< 1/2\]
d) Both b and c
Explanation:
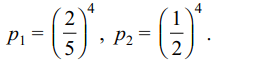
5. I wrote a letter to my friend X and gave it to my son
to post it. The probability that my son will forget to
post the letter is 1/10 and the letter will be lost in
the post is 1/100. If my friend X did not receive the
letter, then the probability that
a) my son forgot to post the letter is 891/1000
b) the letter was lost in the post 891/991
c) my son forgot to post the letter is 100/991
d) Both a and b
Explanation:
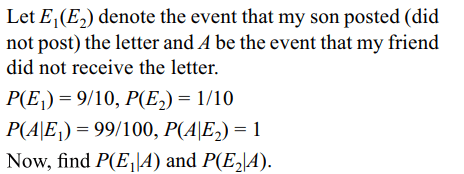
6. A number x is chosen at random from the first 100 natural
numbers. the probability that is satisfies
a) \[x^{2}-25x\leq 150\] is 0.3
b) \[x^{2}-17x+ 30\geq 0\] is 0.88
c) \[30x-x^{2}\] is a perfect square of a natural number is 0.07.
d) All of the Above
Explanation:
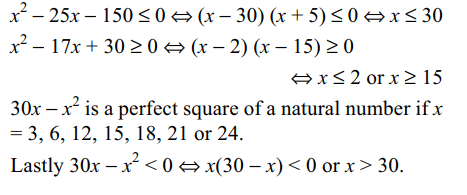
7. Two fair dice are thrown. The probability that difference
between the number is
a) two is 2/9
b) three is 1/6
c) at least two is 1/2
d) All of the Above
Explanation: Difference is two if the outcomes are
(1, 3) (2, 4), (3, 5), (4, 6), (3, 1), (4, 2), (5, 3), (6, 4).
Similarly for others
8. I post a letter to my friend and do not receive a reply.
It is known that one letter out of m letters do not
reach its destination. If it is certain that my friend
will reply if he receives the letter. If A denotes the
event that my friend receives the letter and B that I
get a reply, then
a) \[P\left(B\right) = \left(1 - 1/m\right)^{2}\]
b) \[P\left(A \cap B\right) = \left(1 - 1/m\right)^{2}\]
c) \[P\left(A \mid B'\right) = \left(m - 1\right)/\left(2m - 1\right)\]
d) All of the Above
Explanation:
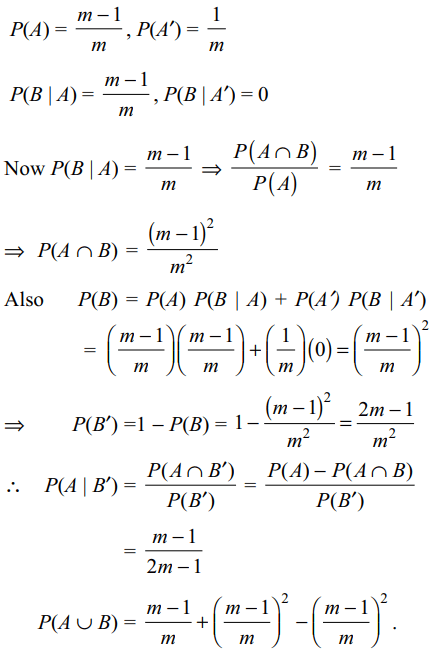
9. An electric component manufactured by ‘KIAAN Electronics’
is tested for its defectiveness by a sophisticated
testing device. Let A denote the event
“the device is defective” and B the event “the testing
device reveals the component to be defective”.
Suppose \[P\left(A\right) = \alpha\] and \[P\left(B\mid A\right) = P\left(B'\mid A'\right)=1-\alpha\] ,
where \[0<\alpha < 1\] , then
a) \[P\left(B\right) = 2\alpha\left(1-\alpha\right)\]
b) \[P\left(A' \mid B\right) =1/2\]
c) \[P\left(B'\right) = \left(1-\alpha\right)^{2}\]
d) All of the Above
Explanation:
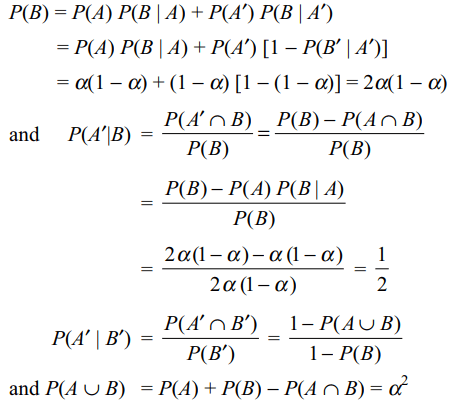
10. Suppose X is a random variable which takes values
0, 1, 2, 3, .... and \[P\left(X=r\right) =pq^{r}\] where 0 < p < 1, q
= 1 – p and r = 0, 1, 2, .... Then
a) \[P\left(X\geq n\right) =q^{n}\]
b) \[P\left(X\geq m+n\mid X \geq m\right) =P\left(X \geq n\right)\]
c) \[P\left(X= m+n\mid X \geq m\right) =P\left(X = n\right)\]
d) All of the Above
Explanation: