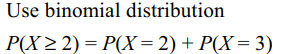1. Let X and Y be two events such that \[P\left( X\mid Y\right)=\frac{1}{2},P\left( Y\mid X\right)=\frac{1}{3}\] and \[P\left( X\cap Y\right)=\frac{1}{6}\] Which of the
following is(are) correct?
a) \[ P\left( X\cap Y\right)=\frac{2}{3}\]
b) X and Y are independent
c) X and Y are not independent
d) Both a and b
Explanation:
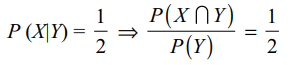
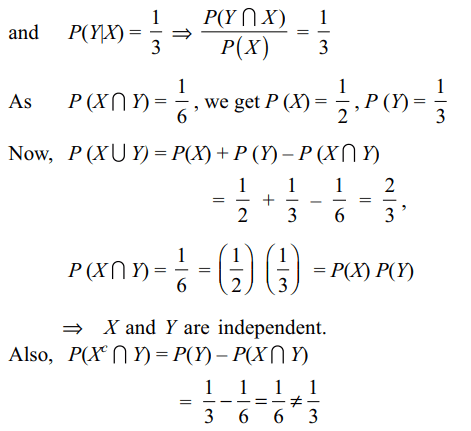
2. Three numbers are chosen at random
without replacement from {1, 2, ...., 15}. Let \[E_{1}\] be the
event that minimum of the chosen numbers is 5 and \[E_{2}\]
their maximum is 10 then
a) \[P\left(E_{1}\right)=\frac{9}{91}\]
b) \[P\left(E_{2}\right)=\frac{36}{455}\]
c) \[P\left(E_{1} \cap E_{2}\right)=\frac{4}{455}\]
d) All of the Above
Explanation:
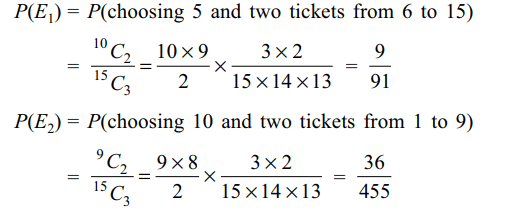
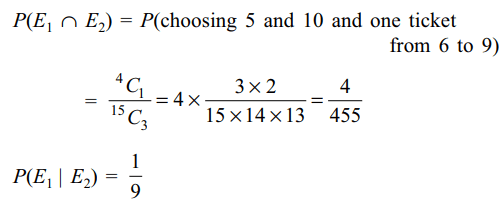
3. A group consists 2n students including you and
your friend. If the group is split into two different
sections A and B, each containing n students, then
the probability that you and your friend are in the
different sections is
a) \[\frac{n}{2n-1}\]
b) \[\frac{n-1}{2n-1}\]
c) \[\frac{n+1}{2n-1}\]
d) \[\frac{2}{2n-1}\]
Explanation:

4. Two persons A and B think of two numbers at random
from the numbers 1, 2, …, n. Probability A
think of a number smaller than thought by B is
a) \[\frac{n-1}{2n}\]
b) \[\frac{2n-1}{2n}\]
c) \[\frac{n-1}{2n}\]
d) \[\frac{n}{2n-1}\]
Explanation:
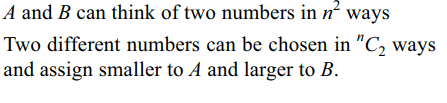
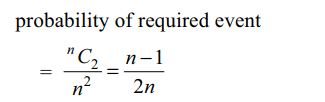
5. A box contains 20 cards of these 10 have letter J
printed on them and the remaining 10 have E printed on them. 3 cards are drawn from the box, the
probability that we can write JEE with these cards is
a) 9/80
b) 1/8
c) 4/27
d) 15/38
Explanation:
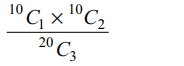
6. A and B toss a coin alternatively till one of them gets
a head and wins the game. If A begins the game, the
probability B wins the game is
a) 1/2
b) 1/3
c) 1/4
d) 2/3
Explanation:
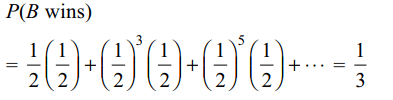
7. A fair coin is tossed repeatedly. If head and tail appear alternatively on first 7 tosses ; then the probability
that head appears on the eighth toss is
a) 1/2
b) 1/128
c) 1/256
d) 7/256
Explanation: Events are independent
8. If P(A) > 0, then the event A is independent of itself
if and only if P(A) is
a) 1/3
b) 1/2
c) 1
d) \[\left(\sqrt{5}-1\right)/2\]
Explanation:
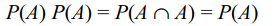
9. Two numbers are selected at random from 1, 2, 3,…,
100 and are multiplied, then the probability (correct
to two places of decimals) that the product thus obtained
is divisible by 3 is
a) 0.22
b) 0.33
c) 0.44
d) 0.55
Explanation: Find the probability of the complement event
0.55
10. The probability that an event A occurrs in a single
trial of an experiment is 0.6. Three independent trials
of the experiment are performed. The probability
that the event A occurs at least twice is
a) 0.636
b) 0.632
c) 0.648
d) 0.946
Explanation: