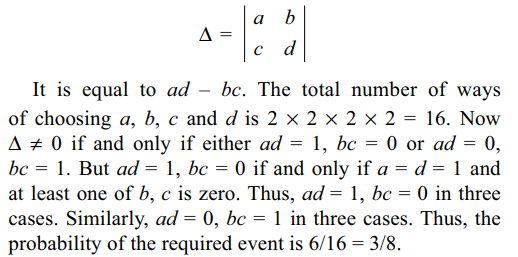1. A fair coin is tossed 2019 times.
Probability of getting at least 1010 heads is
a) \[\frac{1}{2}\]
b) \[\frac{1}{4}\]
c) \[\frac{1}{2^{1009}}\]
d) \[\frac{1}{2^{1010}}\]
Explanation: Let n = 1009, then 2n + 1 = 2019
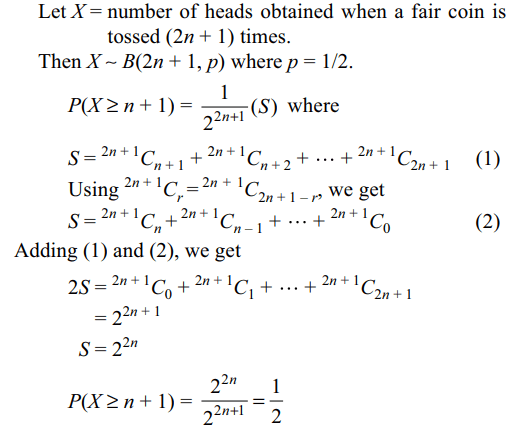
2. From the first 3n(n ≥ 2) natural numbers
two numbers are picked up at random without replacement.
Let P denote the probability that the absolute value of the
difference between the numbers is less than n, then P is
equal to
a) \[\frac{2\left(n-1\right)}{3n-1}\]
b) \[\frac{5\left(n-1\right)}{3\left(3n-1\right)}\]
c) \[\frac{n-1}{3n-1}\]
d) \[\frac{n+1}{3\left(3n-1\right)}\]
Explanation: Two numbers a, b from first 3n natural numbers


3. A box conatins 2n cards numbered \[2^{0},2^{1},2^{2},....,2^{2n-1}\] . Two cards are taken out at random from the
box, at random without replacement. Probability that sum
of the numbers on the card is divisible by 3 is
a) \[\frac{n}{2n-1}\]
b) \[\frac{n-1}{2n-1}\]
c) \[\frac{n+1}{2n}\]
d) \[\frac{1}{2}\]
Explanation: Let the smaller card bear number a and the
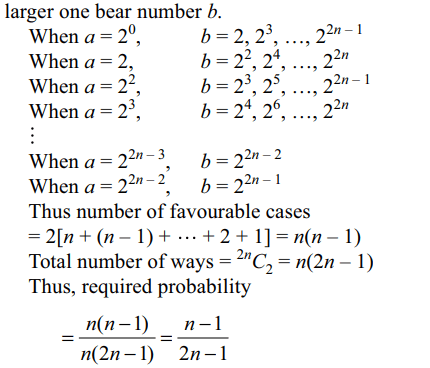
4. An unbiased cubical die is thrown n times.
If \[x_{i}\]= outcome on the ith throw and\[X=gcd \left(x_{1},x_{2},...., x_{n}\right)\] ,
then E(X) is equal to
a) \[\frac{1}{6^{n}}\left(6^{n}+3^{n}+2^{n}\right)\]
b) \[\frac{1}{6^{n}}\left(6^{n}+3^{n}+2^{n}+1\right)\]
c) \[\frac{1}{6^{n}}\left(6^{n}+3^{n}+2^{n+1}+8\right)\]
d) \[\frac{1}{6^{n}}\left(6^{n}+3^{n}+2^{n+2}+8\right)\]
Explanation: Sample space of the random experiment is
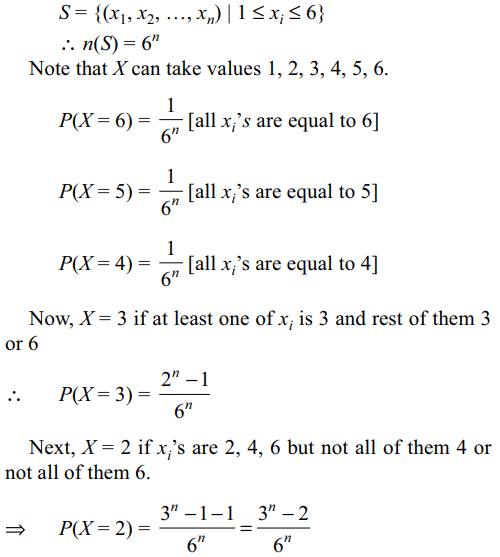
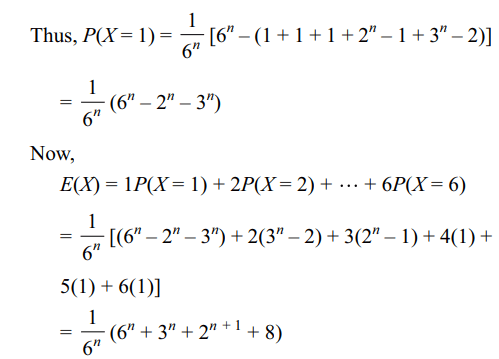
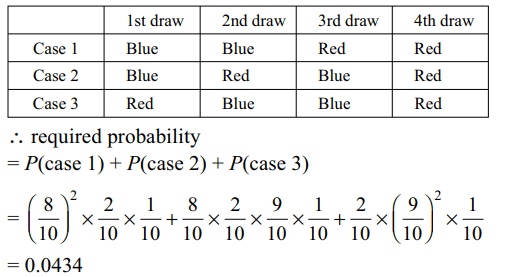
5. There are 8 blue and 2 red balls in a bag.
Each time one ball is drawn and replaced by a blue one.
The probability of drawing the last red ball on the fourth
draw is
a) 0.0434
b) 0.0438
c) 0.0444
d) 0.0453
Explanation:
6. There are m persons sitting in a row. Two
of them are selected at random. The probability that the
two selected persons are not together is
a) 2/m
b) 1/m
c) \[\frac{m\left(m-1\right)}{\left(m+1\right)\left(m+2\right)}\]
d) \[1-\frac{2}{m}\]
Explanation: The total number of ways of selecting two persons out of m is

7. Three six-faced fair dice are thrown
together. The probability that the sum of the numbers
appearing on the dice is \[k\left(3\leq k\leq8\right)\] is
a) \[\frac{\left(k-1\right)\left(k-2\right)}{432}\]
b) \[\frac{k\left(k-1\right)}{432}\]
c) \[\frac{k^{2}}{432}\]
d) \[k^{2}/216\]
Explanation:

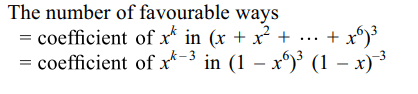
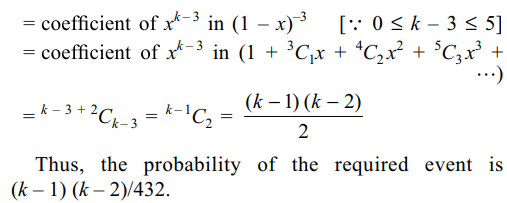
8. Two squares are chosen at random on
a chessboard. The probability that they have a side in
common is
a) 1/9
b) 2/7
c) 1/18
d) 2/9
Explanation:

9. A bag contains a white and b black balls.
Two players, A and B alternately draw a ball from the bag,
replacing the ball each time after the draw till one of them
draws a white ball and wins the game. A begins the game.
If the probability of A winning the game is three times that
of B, the ratio a : b is
a) 1 : 1
b) 1 : 2
c) 2 : 1
d) 1 : 3
Explanation: Let W denote the event of drawing a white ball at any draw and B that for a black ball. Then
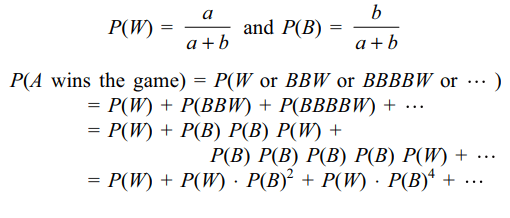
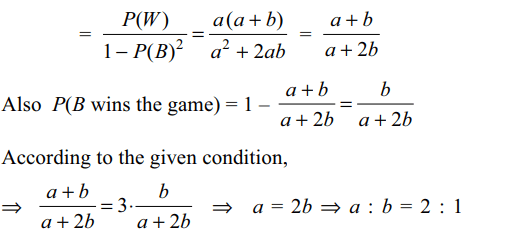
10. A determinant is chosen at random from
the set of all determinants of order 2 with elements 0 or 1
only. The probability that the determinant chosen is nonzero
is
a) 3/16
b) 3/8
c) 1/4
d) 1/8
Explanation: A determinant of order 2 is of the form