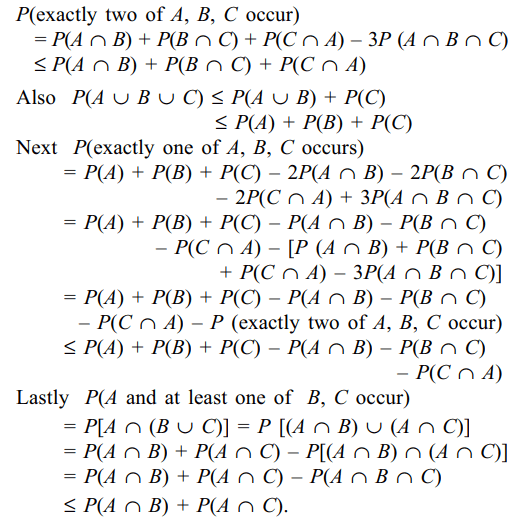1. A group of 6 boys and 6 girls is randomly
divided into two equal groups. The probability that each
group contains 3 boys and 3 girls is
a) 10/231
b) 5/231
c) 90/231
d) 100/231
Explanation: The number of ways of choosing 6 persons out
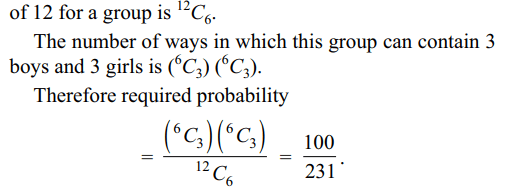
2. In a hurdle race, a runner has probability
p of jumping over a specific hurdle . Given that in 5 trials,
the runner succeeded 3 times, the conditional probability
that the runner had succeeded in the first trial is
a) \[\frac{3}{5}\]
b) \[\frac{2}{5}\]
c) \[\frac{1}{5}\]
d) \[\frac{4}{5}\]
Explanation: Let A denote the event that the runner succeeds
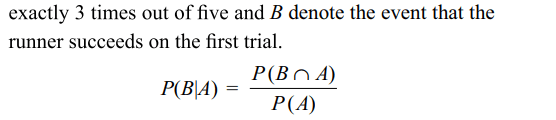
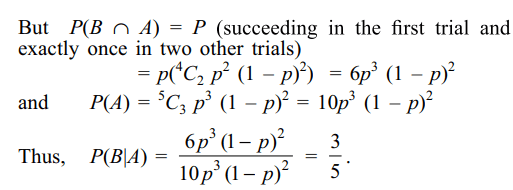
3. Let F denote the set of all onto functions
from \[A=\left\{a_{1},a_{2},a_{3},a_{4}\right\}\] to \[B=\left\{ x,y,z,\right\}\] . A function f
is chosen at random from F. The probability that f–1{x}
consists of exactly one element is
a) 2/3
b) 1/3
c) 1/6
d) 0
Explanation: Let us first count the number of elements in F
4. Three integers are chosen at random
without replacement from the first 20 integers. The
probability that their product is even is
a) 7/19
b) 2/19
c) 17/19
d) 10/19
Explanation: The product of any number of integers will be
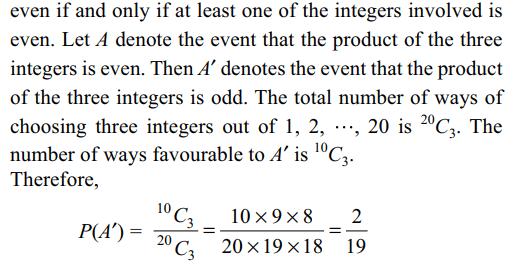
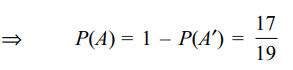
5. A box contains tickets numbered 1 to N.
n tickets are drawn from the box with replacement. The
probability that the largest number on the tickets is k is
a) \[\left(\frac{k}{N}\right)^{n}\]
b) \[\left(\frac{k-1}{N}\right)^{n}\]
c) 0
d) \[\frac{k^{n}-\left(k-1\right)^{n}}{N^{n}}\]
Explanation: Let X denote the largest number on the n tickets
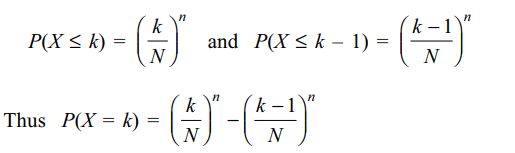drawn.
6. A biased cubical die is thrown twice. Let
P = probability of getting the same number both the
times.
Q= probability getting odd number on the first thrw
and an even number on the second throw.
Then
a) \[Q \leq\frac{1}{4}\]
b) \[P \geq\frac{1}{3}-\frac{2}{3}Q\]
c) \[P +2Q\leq 1\]
d) All of the Above
Explanation: Let pi = probability of getting number i on the
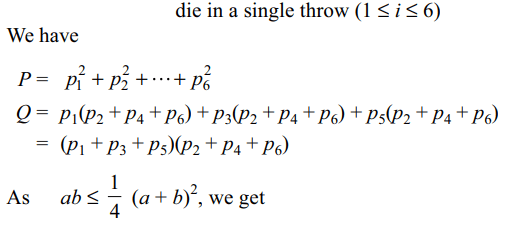
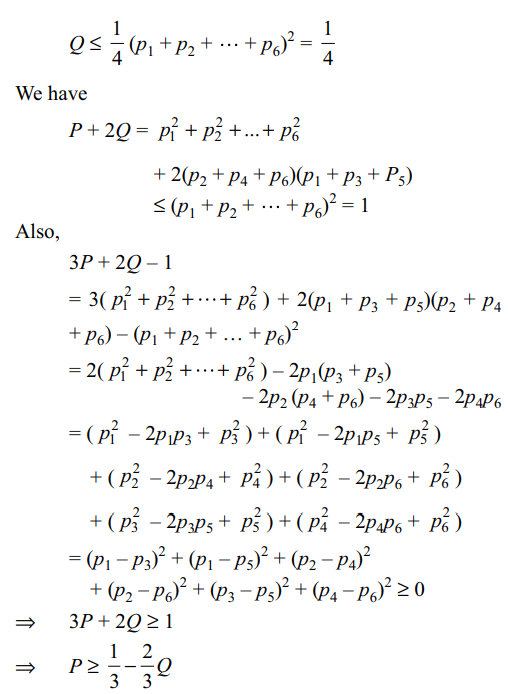
7. An unbiased cubical die is thrown 2n
times, and let P denote the probability of getting even
numbers at least n times, then
a) \[P >\frac{1}{2}\]
b) \[P \geq\frac{1}{2}+\frac{1}{4n}\]
c) \[P =\frac{163}{256}\] if n=4
d) All of the Above
Explanation: Let p = probability of getting an even number on a single throw of the die
and let X = number of times an even number is obtained
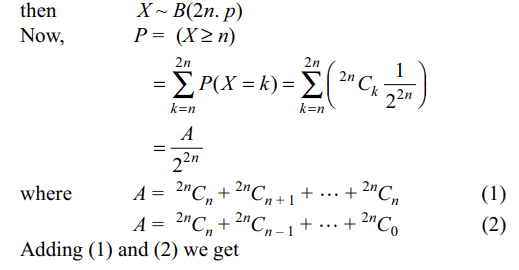
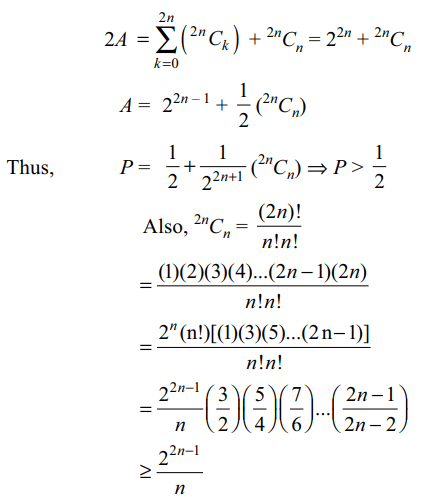
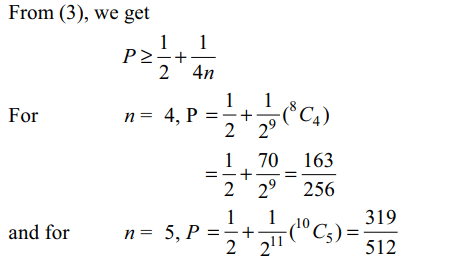
8. If A and B are two events, the probability
that exactly one of them occurs is given by
a) \[P\left(A\right)+P\left(B\right)-2P\left(A\cap B\right)\]
b) \[P\left(A\cap B'\right)+P\left(A'\cap B\right)\]
c) \[P\left(A\cup B\right)-P\left(A\cap B\right)\]
d) All of the Above
Explanation: We have P(exactly one of A, B occurs)
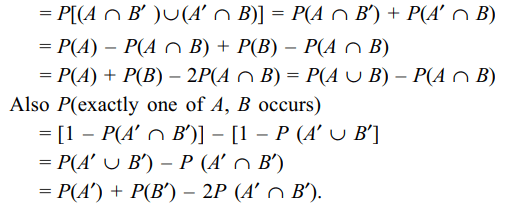
9. If A and B are two events such that
P(A) = 1/2 and P(B) = 2/3, then
a) \[P\left(A\cup B\right)\geq 2/3\]
b) \[P\left(A\cap B'\right)\leq 1/3\]
c) \[1/16\leq P\left(A\cap B\right)\leq 1/2\]
d) All of the Above
Explanation:
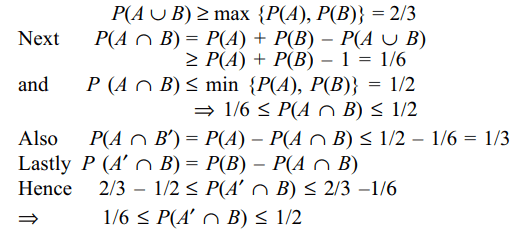
10. If A, B and C are three events, then
a) P (exactly two of A, B, C occur) \[\leq P\left(A \cap B\right) + P\left(B \cap C\right) + P\left(C \cap A\right)\]
b) \[P\left(A\cup B \cup C\right) \leq P\left(A\right) + P\left(B\right) + P\left(C\right)\]
c) P (exactly one of A, B, C occur)
\[\leq P\left(A\right) + P\left(B\right) + P\left(C\right)
– P\left(B \cap C\right) – P\left(C\cap A\right) – P\left(A \cap B\right)\]
d) All of the Above
Explanation:
