1. One mole of monoatomic gas and three moles of diatomic gas are put together in a container. The molar specific heat \[\left( J K^{-1}mol ^{-1}\right)\] at constant
volume is \[\left(R=8.3 J K^{-1}mol ^{-1}\right)\]
a) 18.7
b) 18.9
c) 19.2
d) None of the above
Explanation:
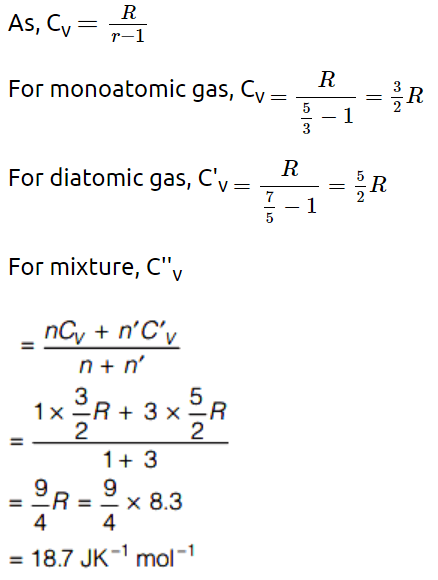
2. The temperature of argon, kept in a vessel, is raised by \[1 ^{\circ}C\] at a constant volume. The total heat supplied to the gas is a combination of
translational and rotational energies. Their respective shares are
a) 60% and 40%
b) 40% and 60%
c) 50% and 50%
d) 100% and 0%
Explanation: 100% and 0%
3. On giving equal amount of heat at constant volume to 1 mol of a monoatomic and a diatomic gas the rise in temperature \[\left(\triangle T\right)\] is more for
a) Monoatomic
b) Diatomic
c) Same for both
d) Can not be predicted
Explanation: Monoatomic
4. The kinetic energy, due to translational motion, of
most of the molecules of an ideal gas at absolute
temperature T is
a) kT
b) k/T
c) T/k
d) 1/kT
Explanation: kT
5. The number of translational degrees of freedom for a diatomic gas is
a) 2
b) 3
c) 5
d) 6
Explanation: The number of translational degrees of freedom for a diatomic gas is 3
6. The value of the gas constant (R) calculated from the perfect gas equation is 8.32 joules/gm mole K, whereas its value calculated from the knowledge
of \[C_{P}\] and \[C_{v}\] of the gas is 1.98 cal/gm mole K. From this data, the value of J is
a) 4.16 J / cal
b) 4.18 J / cal
c) 4.20 J / cal
d) 4.22 J / cal
Explanation: 4.20 J / cal
7. For a gas if ratio of specific heats at constant pressure and volume is \[\gamma\] then value of degrees of
freedom is
a) \[\frac{3\gamma-1}{2\gamma-1}\]
b) \[\frac{2}{\gamma-1}\]
c) \[\frac{9}{2}{\gamma-1}\]
d)\[\frac{25}{2}{\gamma-1}\]
Explanation: For a gas if ratio of specific heats at constant pressure and volume is \[\gamma\] then value of degrees of freedom is \[\frac{2}{\gamma-1}\]
8. The ratio of specific heat of a mixture of one mole of helium and one mole of hydrogen gas will be
a) 1
b) 1.5
c) 1.53
d) 1.33
Explanation: The ratio of specific heat of a mixture of one mole of helium and one mole of hydrogen gas will be 1.5
9. For a gas \[\gamma=7\diagup5\] . The gas may probably be
a) Helium
b) Hydrogen
c) Argon
d) Neon
Explanation: For a gas \[\gamma=7\diagup5\] . The gas may probably be Hydrogen
10. If a gas has n degrees of freedom ratio of specific heats of gas is
a) \[\frac{1+n}{2}\]
b) \[1+\frac{1}{n}\]
c) \[1+\frac{n}{2}\]
d) \[1+\frac{2}{n}\]
Explanation: If a gas has n degrees of freedom ratio of specific heats of gas is \[1+\frac{2}{n}\]
11. The mean kinetic energy of a gas at 300 K is 100 J. The mean energy of the gas at 450 K is equal to
a) 100 J
b) 3000 J
c) 450 J
d) 150 J
Explanation:

12. The capacity of a vessel is 3 litres. It contains 6 gm oxygen, 8 gm nitrogen and 5 gm \[CO_{2}\] mixture at 27°C. If R = 8.31 \[J/mole\times kelvin\] , then the
pressure in the vessel in \[N\diagup m^{2}\] will be (approx.)
a) \[5\times10^{5}\]
b) \[5\times10^{4}\]
c) \[10^{6}\]
d) \[10^{5}\]
Explanation:

13. In the absence of intermolecular force of attraction, the observed pressure P will be
a) P
b) < P
c) > P
d) Zero
Explanation: In the absence of intermolecular force of attraction, the observed pressure P will be > P
14. Two ideal gases at absolute temperature \[T_{1}\] and \[T_{2} \] are mixed. There is no loss of energy. The masses of the molecules are \[m_{1}\] and \[m_{2} \] and the number of
molecules in the gases are \[n_{1}\] and \[n_{2} \] respectively. The temperature of mixture will be
a) \[\frac{T_{1} + T_{2} }{2}energy\]
b) \[\frac{T_{1} + T_{2} }{n_{1} n_{2}}\]
c) \[\frac{n_{1}T_{1} +n_{2} T_{2} }{n_{1}+ n_{2}}\]
d) \[\left(T_{1} + T_{2}\right)\]
Explanation: \[\frac{n_{1}T_{1} +n_{2} T_{2} }{n_{1}+ n_{2}}\]
15. The molecules of an ideal gas at a certain temperature have
a) Only potential energy
b) Only kinetic energy
c) Potential and kinetic energy both
d) None of the above
Explanation: The molecules of an ideal gas at a certain temperature have only kinetic energy
16. Mean kinetic energy per degree of freedom of gas molecules is
a) \[\frac{3}{2}kT\]
b) kT
c) \[\frac{1}{2}kT\]
d) \[\frac{3}{2}RT\]
Explanation: Mean kinetic energy per degree of freedom of gas molecules is \[\frac{1}{2}kT\]
17. The temperature at which the average translational kinetic energy of a molecule is equal to the energy gained by an electron in
accelerating from rest through a potential difference of 1 volt is
a) \[4.6\times 10^{3}K\]
b) \[11.6\times 10^{3}K\]
c) \[23.2\times 10^{3}K\]
d) \[7.7\times 10^{3}K\]
Explanation:
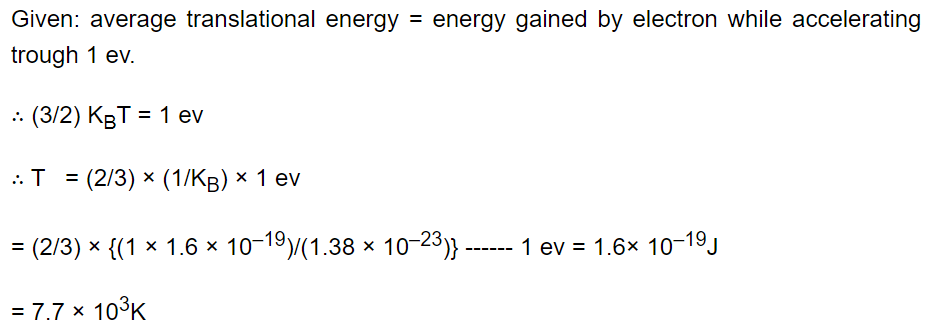
18. The kinetic energy of one gm-mole of a gas at normal temperature and pressure is (R = 8.31
J/Mole-K)
a) \[0.56\times 10^{4}J\]
b) \[1.3\times 10^{2}J\]
c) \[2.7\times 10^{2}J\]
d) \[3.4\times 10^{3}J\]
Explanation:
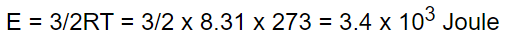
19. The average kinetic energy of hydrogen molecules at 300 K is E. At the same temperature, the average kinetic energy of oxygen molecules will
be
a) E/4
b) E/16
c) E
d) 4 E
Explanation: The average kinetic energy of hydrogen molecules at 300 K is E. At the same temperature, the average kinetic energy of oxygen molecules will be E
20. The average translational kinetic energy of a hydrogen gas molecules at NTP will be
[Boltzmann’s constant \[K_{B}=1.38\times 10^{-23}J\diagup K\] ]
a) \[0.186\times 10^{-20}Joule\]
b) \[0.372\times 10^{-20}Joule\]
c) \[0.56\times 10^{-20}Joule\]
d) \[5.6\times 10^{-20}Joule\]
Explanation:
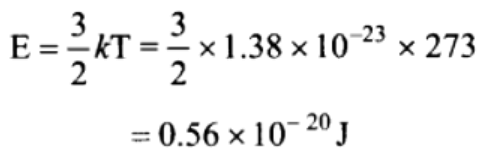
21. In kinetic theory of gases, which of the following statements regarding elastic collisions of the molecules is wrong
a) Kinetic energy is lost in collisions
b) Kinetic energy remains constant in collision
c) Momentum is conserved in collision
d) Pressure of the gas remains constant in collisions
Explanation: Kinetic energy is lost in collisions
22. If r.m.s. velocity of a gas is \[V_{rms}=1840m\diagup s\] and its density \[\rho=8.99\times 10^{-2}kg\diagup m^{3}\] the pressure of the
gas will be
a) \[1.01N\diagup m^{2}\]
b) \[1.01\times 10^{3}N\diagup m^{2}\]
c) \[1.01\times 10^{5}N\diagup m^{2}\]
d) \[1.01\times 10^{7}N\diagup m^{2}\]
Explanation: \[1.01\times 10^{5}N\diagup m^{2}\]
23. An ideal gas is filled in a vessel, then
a) If it is placed inside a moving train, its temperature increases
b) Its centre of mass moves randomly
c) Its temperature remains constant in a moving car
d) None of these
Explanation: An ideal gas is filled in a vessel, then its temperature remains constant in a moving car
24. The kinetic energy of one mole gas at 300K temperature, is E. At 400K temperature kinetic energy is \[E'\] . The value of \[E'\diagup E\] is
a) 1.33
b) \[\sqrt{\left(\frac{4}{3}\right)}\]
c) \[\frac{16}{9}\]
d) 2
Explanation:
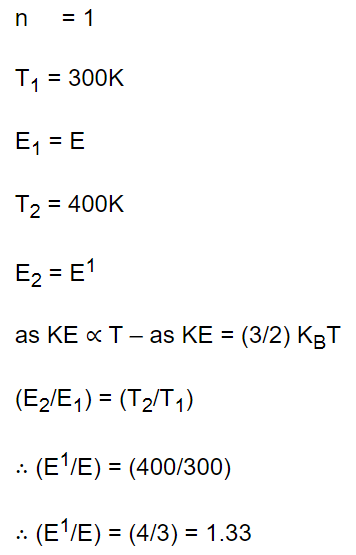
25. N molecules each of mass m of gas A and 2N molecules each of mass 2m of gas B are contained in the same vessel at temperature T. The mean
square of the velocity of molecules of gas B is \[V^{2}\] and the mean square of x component of the velocity of molecules of gas A is \[W^{2}\] . The ratio \[\frac{W^{2}}{V^{2}}\]
a) 1
b) 2
c) \[\frac{1}{3}\]
d) \[\frac{2}{3}\]
Explanation:
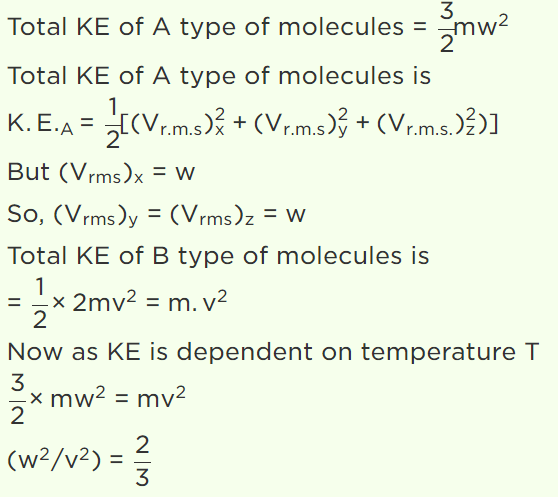
26. A gas is filled in a cylinder, its temperature is increased by 20% on Kelvin scale and volume is reduced by 10%. How much percentage of the gas
will leak out
a) 30%
b) 40%
c) 15%
d) 25%
Explanation:
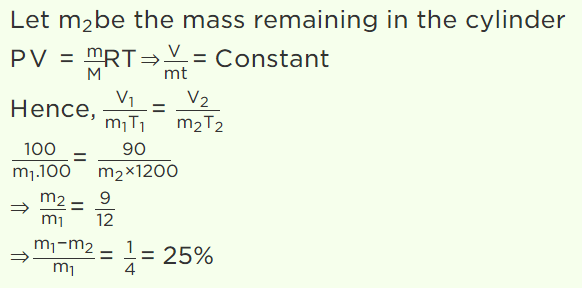
27. The air density at Mount Everest is less than that at the sea level. It is found by mountaineers that for one trip lasting a few hours, the extra oxygen
needed by them corresponds to 30,000 cc at sea level (pressure 1 atmosphere, temperature 27°C). Assuming that the temperature around Mount
Everest is –73°C and that the oxygen cylinder has capacity of 5.2 litre, the pressure at which \[O_{2}\] be filled (at site) in cylinder is
a) 3.86 atm
b) 5.00 atm
c) 5.77 atm
d) 1 atm
Explanation:

28. \[\frac{1}{2} mole\] of helium gas is contained in a container at S.T.P. The heat energy needed to double the pressure of the gas, keeping the volume constant (specific heat of the gas \[=3 J gm^{-1}K^{-1}\] )
a) 3276 J
b) 1638 J
c) 819 J
d) 409.5 J
Explanation:
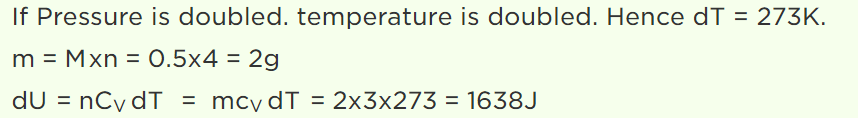
29. The equation of state of a gas is given by \[\left(P+\frac{aT^{2}}{V}\right)V^{C}=\left(RT+b\right)\] , where a, b, c and R are constants. The isotherms can be represented by
\[P=AV^{m}-BV^{n}\] , where A and B depend only on temperature and
a) m=-c and n=-1
b) m=c and n=1
c) m=-c and n=1
d) m=c and n=-1
Explanation: m=-c and n=-1
30. From the following statements, concerning ideal gas at any given temperature T, select the correct one(s)
a) The coefficient of volume expansion at constant pressure is same for all ideal gases
b) In a gaseous mixture, the average translational kinetic energy of the molecules of each component is same
c) The mean free path of molecules increases
with the decrease in pressure
d) All of the above
Explanation: All of the above
31. 70 calories of heat are required to raise the temperature of 2 moles of an ideal gas at constant pressure from 30°C to 35°C. The amount of heat required to raise the temperature of same gas
through the same range (30°C to 35°C) at constant volume (R = 2 cal/mol/K)
a) 30 cal
b) 50 cal
c) 70 cal
d) 90 cal
Explanation:

32. A closed compartment containing gas is moving with some acceleration in horizontal direction. Neglect effect of gravity. Then the pressure in the
compartment is
a) Same everywhere
b) Lower in the front side
c) Lower in the rear side
d) Lower in the upper side
Explanation: A closed compartment containing gas is moving with some acceleration in horizontal direction. Neglect effect of gravity. Then the pressure in the compartment is lower in the front side
33. Three closed vessels A, B and C are at the same temperature T and contain gases which obey the Maxwellian distribution of velocities. Vessel A contains only \[O_{2}\] , B only \[N_{2}\] and C a mixture of
equal quantities of O2 and \[N_{2}\] . If the average speed of the \[O_{2}\] molecules in vessel A is \[V_{1} \] , that of the \[N_{2}\] molecules in vessel B is \[V_{2} \] , the average
speed of the \[O_{2}\] molecules in vessel C is
a) \[\left(V_{1}+V_{2}\right)\diagup 2\]
b) \[V_{1}\]
c) \[\left(V_{1}V_{2}\right)^{1\diagup 2}\]
d) \[\sqrt{3kT / M}\]
Explanation: \[V_{1}\]
34. A box containing N molecules of a perfect gas at temperature \[T_{1}\] and pressure \[P_{1}\] . The number of molecules in the box is doubled keeping the total kinetic energy of the gas same as before. If the
new pressure is \[P_{2}\] and temperature \[T_{2}\] , then
a) \[P_{2}=P_{1},T_{2}=T_{1}\]
b) \[P_{2}=P_{1},T_{2}=\frac{T_{1}}{2}\]
c) \[P_{2}=2P_{1},T_{2}=T_{1}\]
d) \[P_{2}=2P_{1},T_{2}=\frac{T_{1}}{2}\]
Explanation: \[P_{2}=P_{1},T_{2}=\frac{T_{1}}{2}\]
35. A gas in container A is in thermal equilibrium with another gas in container B. both contain equal masses of the two gases in the respective
containers. Which of the following can be true
a) \[P_{A}V_{A}=P_{B}V_{B}\]
b) \[P_{A}=P_{B},V_{A}\neq V_{B}\]
c) \[P_{A}\neq P_{B},V_{A}= V_{B}\]
d) Both b and c
Explanation: Both b and c
36. Two containers of equal volume contain the same gas at pressures \[P_{1}\] and \[P_{2}\] and absolute temperatures \[T_{1}\] and \[T_{2}\] respectively. On joining
the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
a) \[\frac{P_{1}}{T_{1}}+\frac{P_{2}}{T_{2}}\]
b) \[\frac{P_{1}T_{1}+P_{2}T_{2}}{\left(T_{1}+T_{2}\right)^{2}}\]
c) \[\frac{P_{1}T_{2}+P_{2}T_{1}}{\left(T_{1}+T_{2}\right)^{2}}\]
d) \[\frac{P_{1}}{2T_{1}}+\frac{P_{2}}{2T_{2}}\]
Explanation: \[\frac{P_{1}}{2T_{1}}+\frac{P_{2}}{2T_{2}}\]
37. At the top of a mountain a thermometer reads 7°C and a barometer reads 70 cm of Hg. At the bottom of the mountain these read 27°C and 76 cm of Hg
respectively. Comparison of density of air at the top with that of bottom is
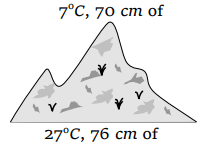
a) 75/76
b) 70/76
c) 76/75
d) 76/70
Explanation: 75/76
38. The root mean square speed of the molecules of a diatomic gas is v. When the temperature is doubled, the molecules dissociate into two atoms.
The new root mean square speed of the atom is
a) \[\sqrt{2v}\]
b) v
c) 2v
d) 4v
Explanation:
39. A vessel is partitioned in two equal halves by a fixed diathermic separator. Two different ideal gases are filled in left (L) and right (R) halves.
The rms speed of the molecules in L part is equal to the mean speed of molecules in the R part. Then the ratio of the mass of a molecule in L part
to that of a molecule in R part is
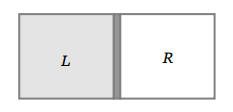
a) \[\sqrt{\frac{3}{2}}\]
b) \[\sqrt{\pi\diagup 4}\]
c) \[\sqrt{2\diagup 3}\]
d) \[3\pi\diagup 8\]
Explanation:

40. A gas is filled in the cylinder shown in the figure. The two pistons are joined by a string. If the gas
is heated, the pistons will
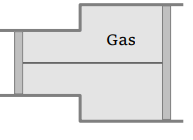
a) Move towards left
b) Move towards right
c) Remain stationary
d) None of these
Explanation: The two pistons are joined by a string. If the gas is heated, the pistons will move towards right
41. A closed vessel contains 8gm of oxygen and 7gm of nitrogen. The total pressure is 10 atm at a given temperature. If now oxygen is absorbed by
introducing a suitable absorbent the pressure of the remaining gas in atm will be
a) 2
b) 10
c) 4
d) 5
Explanation:
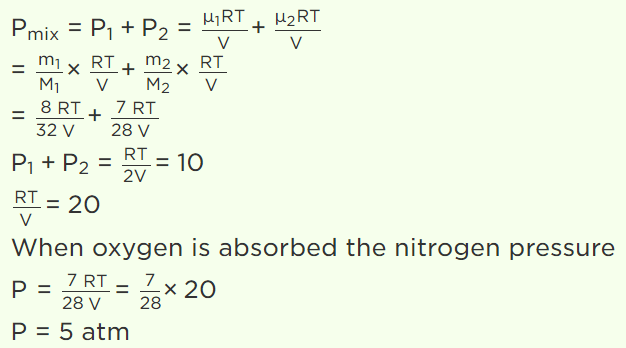
42. \[CO_{2}\left(O-C-O\right)\] is a triatomic gas. Mean kinetic energy of one gram gas will be (If N-Avogadro's number, k-Boltzmann's constant and molecular
weight of \[CO_{2}=44\] )
a) (3 / 88)NkT
b) (5 / 88)NkT
c) (6 / 88)NkT
d) (7 / 88)NkT
Explanation:
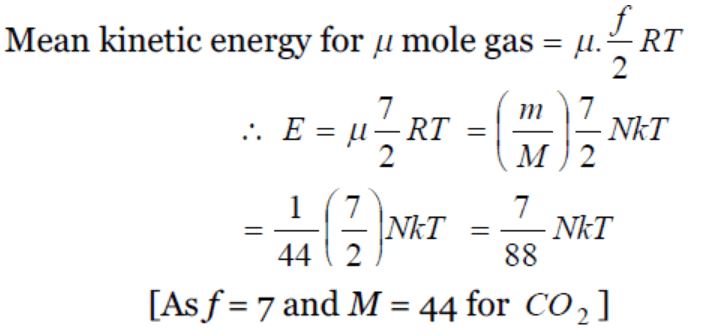
43. 40 calories of heat is needed to raise the temperature of 1 mole of an ideal monoatomic gas from 20°C to 30°C at a constant pressure. The
amount of heat required to raise its temperature over the same interval at a constant volume ( R = 2 calorie \[mole^{-1}K^{-1}\] ) is
a) 20 calorie
b) 40 calorie
c) 60 calorie
d) 80 calorie
Explanation:
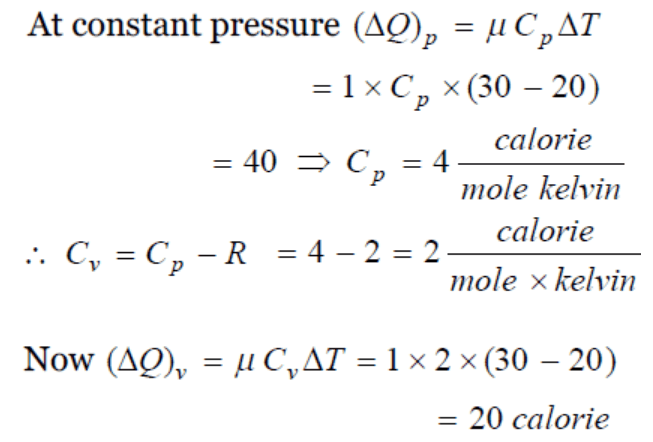
44. The pressure and volume of saturated water vapour are P and V respectively. It is compressed isothermally thereby volume becomes V/2, the
final pressure will be
a) More than 2P
b) P
c) 2P
d) 4P
Explanation: The pressure and volume of saturated water vapour are P and V respectively. It is compressed isothermally thereby volume becomes V/2, the final pressure will be P
45. If the intermolecular forces vanish away, the volume occupied by the molecules contained in 4.5 kg water at standard temperature and pressure will be
a) \[5.6 m^{3}\]
b) \[4.5 m^{3}\]
c) 11.2 litre
d) \[11.2 m^{3}\]
Explanation:
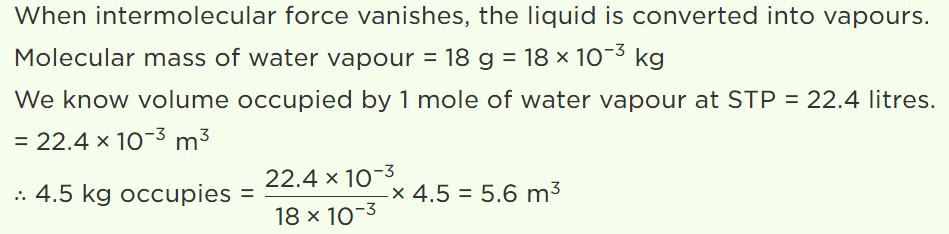
46. When an air bubble of radius ‘r’ rises from the bottom to the surface of a lake, its radius becomes 5r/4 (the pressure of the atmosphere is equal to the 10 m height of water column). If the
temperature is constant and the surface tension is neglected, the depth of the lake is
a) 3.53 m
b) 6.53 m
c) 9.53 m
d) 12.53 m
Explanation: The depth of the lake is 9.53 m
47. A horizontal uniform glass tube of 100 cm, length sealed at both ends contain 10 cm mercury column in the middle. The temperature and pressure of
air on either side of mercury column are respectively 81°C and 76 cm of mercury. If the air column at one end is kept at 0°C and the other end at 273°C, the pressure of air which is at 0°C is (in cm of Hg)
a) 76
b) 68.2
c) 102.4
d) 122
Explanation: 102.4
48. At standard temperature and pressure the density of a gas is \[1.3 kg / m^{3}\] and the speed of the sound in gas is 330 m/sec. Then the degree of freedom of
the gas will be
a) 3
b) 4
c) 5
d) 6
Explanation:
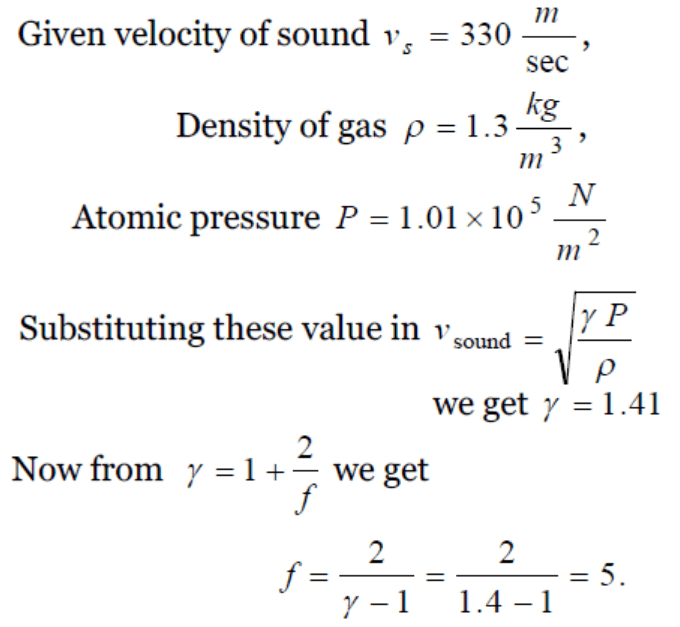
49. The temperature of 5 moles of a gas which was held at constant volume was changed from 100oC to \[120^{\circ} C\] . The change in internal energy was
found to be 80 Joules. The total heat capacity of the gas at constant volume will be equal to
a) 8 J/K
b) 0.8 J/K
c) 4.0 J/K
d) 0.4 J/K
Explanation: 4.0 J/K
50. The temperature at which the r.m.s. speed of hydrogen molecules is equal to escape velocity on
earth surface, will be
a) 1060 K
b) 5030 K
c) 8270 K
d) 10063 K
Explanation:
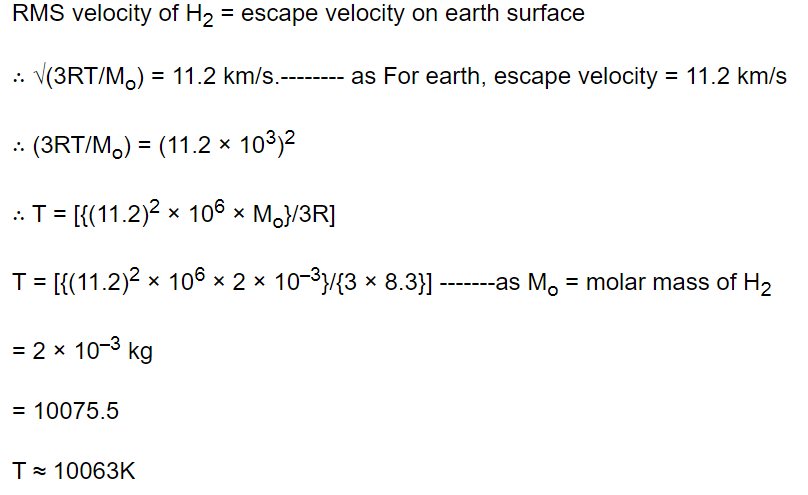
51. Inside a cylinder having insulating walls and closed at ends is a movable piston, which divides the cylinder into two compartments. On one side
of the piston is a mass m of a gas and on the other side a mass 2 m of the same gas. What fraction of volume of the cylinder will be occupied by the larger mass of the gas when the piston is in
equilibrium ? Consider that the movable piston is conducting so that the temperature is the same throughout
a) \[\frac{1}{4}\]
b) \[\frac{1}{3}\]
c) \[\frac{1}{2}\]
d) \[\frac{2}{3}\]
Explanation:

52. The diameter of oxygen molecule is \[2.94\times10^{ -10}m\] . The Vander Waal’s gas constant ‘b’ in \[m^{ 3}\diagup mol\] will
be
a) 3.2
b) 16
c) \[32\times10^{ -4}\]
d) \[32\times10^{ -6}\]
Explanation: \[32\times10^{ -6}\]
53. The temperature of the mixture of one mole of helium and one mole of hydrogen is increased from \[0^{\circ} C\] to \[100^{\circ} C\] at constant pressure. The
amount of heat delivered will be
a) 600 cal
b) 1200 cal
c) 1800 cal
d) 3600 cal
Explanation: 1200 cal
54. A vessel contains a mixture of one mole of oxygen and two moles of nitrogen at 300 K. The ratio of the average rotational kinetic energy per \[O_{2}\]
molecule to that per \[N_{2}\] molecule is
a) 1 : 1
b) 1 : 2
c) 2 : 1
d) Depends on the moments of inertia of the two
molecules
Explanation: A vessel contains a mixture of one mole of oxygen and two moles of nitrogen at 300 K. The ratio of the average rotational kinetic energy per \[O_{2}\] molecule to that per \[N_{2}\] molecule is 1 : 1
55. A vessel contains 14 gm (7 moles) of hydrogen and 96 gm (9 moles) of oxygen at STP. Chemical reaction is induced by passing electric spark in the vessel till one of the gases is consumed. The
temperature is brought back to it's starting value 273 K. The pressure in the vessel is
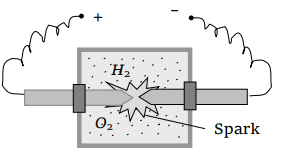
a) 0.1 atm
b) 0.2 atm
c) 0.3 atm
d) 0.4 atm
Explanation:


56.A gas mixture consists of 2 mole of oxygen and 4 mole of argon at temperature T. Neglecting all vibrational modes, the total internal energy of the
system is
a) 4 RT
b) 15 RT
c) 9 RT
d) 11 RT
Explanation: A gas mixture consists of 2 mole of oxygen and 4 mole of argon at temperature T. Neglecting all vibrational modes, the total internal energy of the system is 11 RT
57. A jar contains a gas and few drops of water at T K. The pressure in the jar is 830 mm of mercury. The temperature of jar is reduced by 1%. The saturated vapour pressure of water at the two
temperatures are 30 mm and 25 mm of mercury. Then the new pressure in the jar will be
a) 917 mm of Hg
b) 717 mm of Hg
c) 817 mm of Hg
d) None of these
Explanation:

58. Molar specific heat of oxygen at constant pressure \[C_{P}= 7.2 cal \diagup mol^{\circ} C\] and R = 8.3 joule/mol/K. At constant volume, 5 mol of oxygen is heated from
10°C to 20°C, the quantity of heat required is approximately
a) 25 cal
b) 50 cal
c) 250 cal
d) 500 cal
Explanation: 250 cal
59. One mole of an ideal gas requires 207 J heat to raise the temperature by 10 K when heated at constant pressure. If the same gas is heated at constant volume to raise the temperature by the same 10 K, the heat required is
a) 198.7 J
b) 29 J
c) 215.3 J
d) 124 J
Explanation:
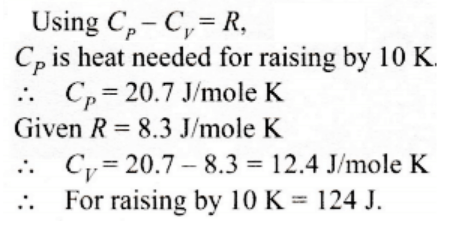
60. The expansion of an ideal gas of mass m at a constant pressure P is given by the straight line D. Then the expansion of the same ideal gas of mass
2m at a pressure P/ 2 is given by the straight line
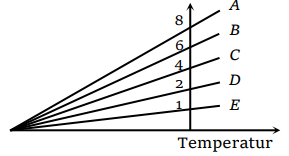
a) E
b) C
c) B
d) A
Explanation: The expansion of an ideal gas of mass m at a constant pressure P is given by the straight line D. Then the expansion of the same ideal gas of mass 2m at a pressure P/ 2 is given by the straight line A