1. At what temperature the molecules of nitrogen will have the same r.m.s. velocity as the molecules of oxygen at 127°C
a) 77°C
b) 350°C
c) 273°C
d) 457°C
Explanation:
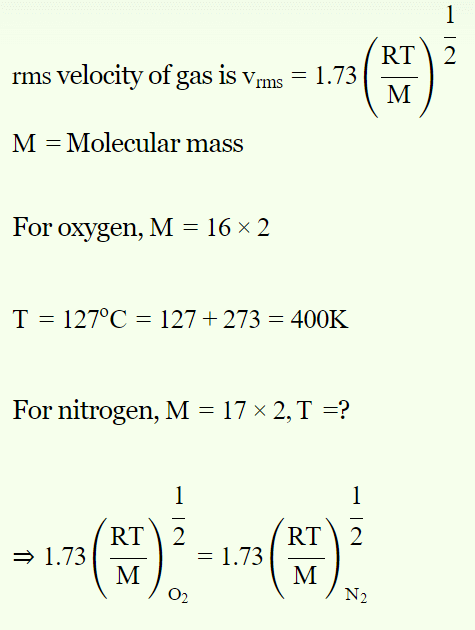
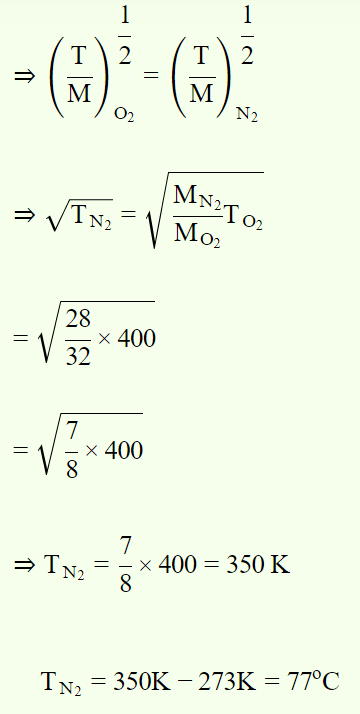
2. r.m.s. velocity of nitrogen molecules at NTP is
a) 492 m /s
b) 517 m/s
c) 546 m/s
d) 33 m/s
Explanation: r.m.s. velocity of nitrogen molecules at NTP is 517 m/s
3. The temperature of the hydrogen at which the average speed of its molecules is equal to that of oxygen molecules at a temperature of 31°C, is
a) – 216°C
b) – 235°C
c) – 254°C
d) – 264°C
Explanation: – 254°C
4.The temperature of an ideal gas is increased from 120 K to 480 K. If at 120 K, the root mean square velocity of the gas molecules is v, at 480 K it
becomes
a) 4v
b) 2v
c) v/2
d) v/4
Explanation:

5. Root mean square velocity of a particle is v at pressure P. If pressure is increased two times, then the r.m.s. velocity becomes
a) 2 v
b) 3 v
c) 0.5 v
d) v
Explanation: Root mean square velocity of a particle is v at pressure P. If pressure is increased two times, then the r.m.s. velocity becomes v
6. The root mean square speed of the molecules of a gas is
a) Independent of its pressure but directly proportional to its Kelvin temperature
b) Directly proportional to the square roots of both its pressure and its Kelvin temperature
c) Independent of its pressure but directly proportional to the square root of its Kelvin temperature
d) Directly proportional to both its pressure and its Kelvin temperature
Explanation: The root mean square speed of the molecules of a gas is independent of its pressure but directly proportional to the square root of its Kelvin temperature
7. At temperature T, the r.m.s. speed of helium molecules is the same as r.m.s. speed of hydrogen
molecules at normal temperature and pressure. The value of T is
a) 273°C
b) 546°C
c) 0°C
d) 136.5°C
Explanation:
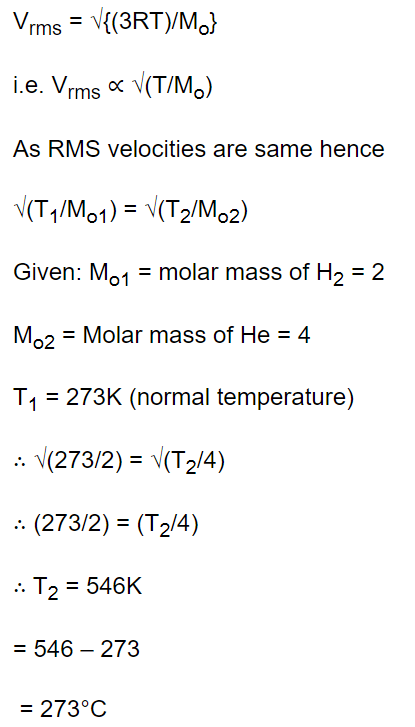
8. The value of densities of two diatomic gases at constant temperature and pressure are \[d_{1}\] and \[d_{2}\] , then the ratio of speed of sound in these gases
will be
a) \[d_{1} d_{2}\]
b) \[\sqrt{d_{2}\diagup d_{1}}\]
c) \[\sqrt{d_{1}\diagup d_{2}}\]
d) \[\sqrt{d_{1} d_{2}}\]
Explanation: The value of densities of two diatomic gases at constant temperature and pressure are \[d_{1}\] and \[d_{2}\] , then the ratio of speed of sound in these gases will be \[\sqrt{d_{2}\diagup d_{1}}\]
9. On any planet, the presence of atmosphere implies ( Crms = root mean square velocity of molecules and Ve = escape velocity)
a) \[C_{rms}\] << \[ V_{e}\]
b) \[C_{rms}>V_{e}\]
c) \[C_{rms}=V_{e}\]
d) \[C_{rms}=0\]
Explanation: \[C_{rms}\] << \[ V_{e}\]
10. In the two vessels of same volume, atomic hydrogen and helium at pressure 1 atm and 2 atm are filled. If temperature of both the samples is
same, then average speed of hydrogen atoms <CH> will be related to that of helium <CHe> as
a) <CH>=5<CHe>
b) <CH>=<CHe>
c) <CH>=2<CHe>
d) None of the above
Explanation: <CH>=2<CHe>