1. Which of the following formulae is wrong
a) \[C_{V}=\frac{R}{\gamma-1}\]
b) \[C_{P}=\frac{\gamma R}{\gamma-1}\]
c) \[C_{P}\diagup C_{V}=\gamma\]
d) \[C_{P}- C_{V}=2R\]
Explanation: This formula is wrong -> \[C_{P}- C_{V}=2R\]
2. For hydrogen gas \[C_{P}- C_{V}=a\] and for oxygen gas \[C_{P}- C_{V}=b\] . So the relation between a and b is given by
a) \[a =16b\]
b) \[b =16a\]
c) \[a =4b\]
d) \[a =b\]
Explanation: \[a =b\]
3. For a gas the difference between the two specific heats is 4150 J/kg K. What is the specific heats at constant volume of gas if the ratio of specific heat
is 1.4
a) 8475 J / kg K
b) 5186 J / kg K
c) 1660 J / kg K
d) 10375 J / kg K
Explanation:
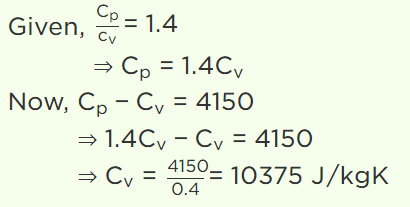
4. The quantity of heat required to raise one mole through one degree Kelvin for a monoatomic gas at constant volume is
a) \[\frac{3}{2}R\]
b) \[\frac{5}{2}R\]
c) \[\frac{7}{2}R\]
d) 4 R
Explanation: The quantity of heat required to raise one mole through one degree Kelvin for a monoatomic gas at constant volume is \[\frac{3}{2}R\]
5. The specific heat relation for ideal gas is
a) \[C_{P}+ C_{V}=R\]
b) \[C_{P}- C_{V}=R\]
c) \[C_{P}\diagup C_{V}=R\]
d) \[C_{V}\diagup C_{P}=R\]
Explanation: The specific heat relation for ideal gas is \[C_{P}- C_{V}=R\]
6. The specific heat of 1 mole of an ideal gas at constant pressure \[\left(C_{P}\right)\] and at constant volume \[\left(C_{V}\right)\] which is correct
a) \[C_{P}\] of hydrogen gas is \[\frac{5}{2}R\]
b) \[C_{V}\] of hydrogen gas is \[\frac{7}{2}R\]
c) \[H_{2}\] has very small values of \[C_{P}\] and \[C_{v}\]
d) \[C_{P} - C_{v}\] = 1.99 cal/mole-K for \[H_{2}\]
Explanation: \[C_{P} - C_{v}\] = 1.99 cal/mole-K for \[H_{2}\]
7. What is the ratio of specific heats of constant pressure and constant volume for \[NH_{3}\]
a) 1.33
b) 1.44
c) 1.28
d) 1.67
Explanation: Ratio of specific heats of constant pressure and constant volume for \[NH_{3}\] is 1.33
8. If two moles of diatomic gas and one mole of mono atomic gas are mixed then the ratio of specific heats is
a) \[\frac{7}{3}\]
b) \[\frac{5}{4}\]
c) \[\frac{19}{13}\]
d) \[\frac{15}{19}\]
Explanation: If two moles of diatomic gas and one mole of mono atomic gas are mixed then the ratio of specific heats is \[\frac{19}{13}\]
9. One mole of ideal monoatomic gas \[\left(\gamma=5\diagup3\right)\] is mixed with one mole of diatomic gas \[\left(\gamma=7\diagup5\right)\] . What is \[\gamma\] for the mixture? \[\gamma\] denotes the ratio of
specific heat at constant pressure, to that at constant volume
a) 3/2
b) 23/15
c) 35/23
d) 4/3
Explanation:
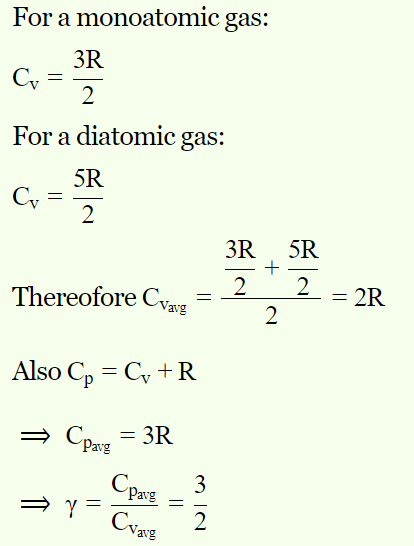
10. A gaseous mixture contains equal number of hydrogen and nitrogen molecules. Specific heat measurements on this mixture at temperatures
below 100 K would indicate that the value of \[\gamma\] (ratio of specific heats) for this mixture is
a) 3/2
b) 4/3
c) 5/3
d) 7/5
Explanation: 5/3
11. 5 moles of oxygen is heated at constant volume from 10°C to 20°C. The change in the internal energy of the gas is (the gram molecular specific
heat of oxygen at constant pressure, \[C_{P}\] = 8 cal/mole °C and R = 8.3 cal/mole °C)
a) 200 cal
b) 300 cal
c) 100 cal
d) None of these
Explanation: 300 cal
12. What is the value of \[\frac{R}{C_{P}}\] for diatomic gas
a) 3/4
b) 3/5
c) 2/7
d) 5/7
Explanation: The value of \[\frac{R}{C_{P}}\] for diatomic gas is 2/7
13. The degrees of freedom of a stationary rigid body about its axis will be
a) One
b) Two
c) Three
d) Four
Explanation: The degrees of freedom of a stationary rigid body about its axis will be 3
14. A gaseous mixture consists of 16g of helium and 16g of oxygen. The ratio \[\frac{C_{P}}{C_{V}}\]
of the mixture is
a) 1.4
b) 1.54
c) 1.59
d) 1.62
Explanation:
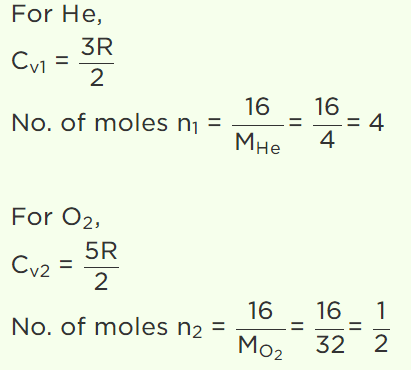
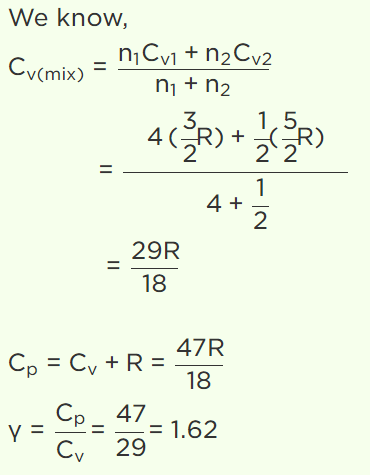
15. The pressure exerted by the gas on the walls of the container because
a) It loses kinetic energy
b) It sticks with the walls
c) On collision with the walls there is a change in momentum
d) It is accelerated towards the walls
Explanation: The pressure exerted by the gas on the walls of the container because on collision with the walls there is a change in momentum
16. Gas at a pressure \[P_{0}\] in contained is a vessel. If the masses of all the molecules are halved and their speeds are doubled, the resulting pressure P
will be equal to
a) \[4P_{0}\]
b) \[2P_{0}\]
c) \[P_{0}\]
d) \[\frac{P_{0}}{2}\]
Explanation:
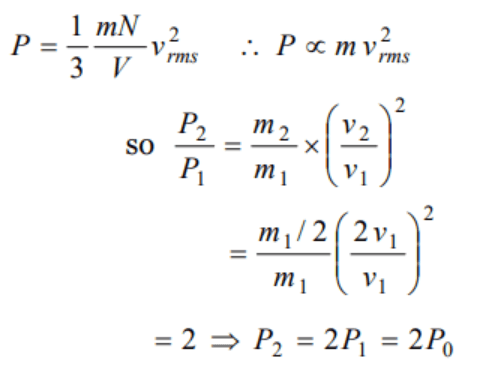
17. A box contains n molecules of a gas. How will the pressure of the gas be effected, if the number of
molecules is made 2n
a) Pressure will decrease
b) Pressure will remain unchanged
c) Pressure will be doubled
d) Pressure will become three times
Explanation: A box contains n molecules of a gas. if the number of molecules is made 2n then pressure will be doubled
18. The relation between the gas pressure P and average kinetic energy per unit volume E is
a) \[P=\frac{1}{2}E\]
b) P = E
c) \[P=\frac{3}{2}E\]
d) \[P=\frac{2}{3}E\]
Explanation: The relation between the gas pressure P and average kinetic energy per unit volume E is \[P=\frac{2}{3}E\]
19. A cylinder of capacity 20 litres is filled with \[H_{2}\] gas. The total average kinetic energy of translatory motion of its molecules is \[1.5\times 10^{5} J\] .
The pressure of hydrogen in the cylinder is
a) \[2\times 10^{6} N\diagup m^{2}\]
b) \[3\times 10^{6} N\diagup m^{2}\]
c) \[4\times 10^{6} N\diagup m^{2}\]
d) \[5\times 10^{6} N\diagup m^{2}\]
Explanation:
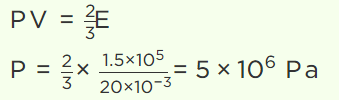
20. The root mean square speed of hydrogen molecules of an ideal hydrogen gas kept in a gas chamber at 0°C is 3180 metres/second. The pressure on the hydrogen gas is (Density of
hydrogen gas is \[8.99\times 10^{-2} kg\diagup m^{3}\] , 1 atmosphere = \[1.01\times 10^{5} N\diagup m^{2}\] )
a) 1.0 atm
b) 1.5 atm
c) 2.0 atm
d) 3.0 atm
Explanation:
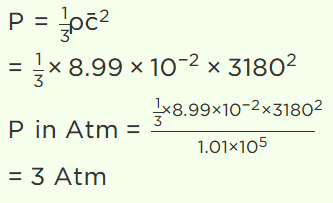
21. At a given temperature, the pressure of an ideal gas of density \[\rho\] is proportional to
a) \[\frac{1}{\rho^{2}}\]
b) \[\frac{1}{\rho}\]
c) \[\rho^{2}\]
d) \[\rho\]
Explanation:
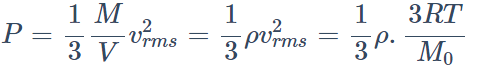
22. Consider a gas with density \[\rho\] and \[\bar{C}\] as the root mean square velocity of its molecules contained in
a volume. If the system moves as whole with velocity v, then the pressure exerted by the gas is
a) \[\frac{1}{3}\rho\bar{C}^{2}\]
b) \[\frac{1}{3}\rho \left(C+V\right)^{2}\]
c) \[\frac{1}{3}\rho \left(C-V\right)^{2}\]
d) \[\frac{1}{3}\rho \left(C^{-2}-V\right)^{2}\]
Explanation: \[\frac{1}{3}\rho\bar{C}^{2}\]
23. If the mean free path of atoms is doubled then the pressure of gas will become
a) P/4
b) P/2
c) P/8
d) P
Explanation: If the mean free path of atoms is doubled then the pressure of gas will become P/2
24. Relationship between P,V, and E for a gas is
a) \[P=\frac{3}{2}EV\]
b) \[V=\frac{2}{3}EP\]
c) \[PV=\frac{3}{2}E\]
d) \[PV=\frac{2}{3}E\]
Explanation: Relationship between P,V, and E for a gas is \[PV=\frac{2}{3}E\]
25. The value of universal gas constant is 8.3 J/mole/K, the mean kinetic energy of 32 gm of
oxygen at – 73°C will be
a) 480 J
b) 4980 J
c) 2490 J
d) The information is incomplete
Explanation:
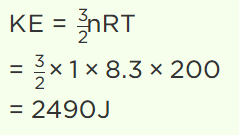
26. For a diatomic gas change in internal energy for unit change in temperature for constant pressure and constant volume is \[U_{1}\] and \[U_{2}\] respectively.
\[U_{1}:U_{2}\] is
a) 5 : 3
b) 3 : 5
c) 1 : 1
d) 5 : 7
Explanation: \[U_{1}:U_{2}\] is 1 : 1
27. If number of molecules of \[H_{2}\] are double than that of \[O_{2}\] , then ratio of kinetic energy of hydrogen
and that of oxygen at 300 K is
a) 1 : 1
b) 1 : 2
c) 2 : 1
d) 1 : 16
Explanation: If number of molecules of \[H_{2}\] are double than that of \[O_{2}\] , then ratio of kinetic energy of hydrogen and that of oxygen at 300 K is 1 : 1
28. The average kinetic energy of a gas at – 23°C and 75 cm pressure is \[5 \times10^{-14}erg\] for \[H_{2}\] . The mean kinetic energy of the \[O_{2}\] at 227°C and 150 cm
pressure will be
a) \[80 \times10^{-14}erg\]
b) \[20 \times10^{-14}erg\]
c) \[40 \times10^{-14}erg\]
d) \[10 \times10^{-14}erg\]
Explanation:

29. The ratio of mean kinetic energy of hydrogen and oxygen at a given temperature is
a) 1 : 16
b) 1 : 8
c) 1 : 4
d) 1 : 1
Explanation: The ratio of mean kinetic energy of hydrogen and oxygen at a given temperature is 1 : 1
30. The ratio of mean kinetic energy of hydrogen and nitrogen at temperature 300 K and 450 K
respectively is
a) 3 : 2
b) 2 : 3
c) 2 : 21
d) 4 : 9
Explanation:
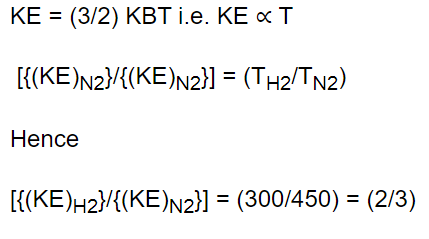
31. According to the kinetic theory of gases, total energy of a gas is equal to
a) Potential energy
b) Kinetic energy
c) Both (a) and (b)
d) None of the above
Explanation: According to the kinetic theory of gases, total energy of a gas is equal to kinetic energy
32. The average kinetic energy of a gas molecule can be determined by knowing
a) The number of molecules in the gas
b) The pressure of the gas only
c) The temperature of the gas only
d) None of the above is enough by itself
Explanation: The average kinetic energy of a gas molecule can be determined by knowing the temperature of the gas only
33. Mean kinetic energy (or average energy) per gm molecule of a monoatomic gas is given by
a) \[\frac{3}{2}RT\]
b) \[\frac{1}{2}KT\]
c) \[\frac{1}{2}RT\]
d) \[\frac{3}{2}KT\]
Explanation: Mean kinetic energy (or average energy) per gm molecule of a monoatomic gas is given by \[\frac{3}{2}RT\]
34. A sealed container with negligible coefficient of volumetric expansion contains helium (a monoatomic gas). When it is heated from 300 K to
600 K, the average K.E. of helium atoms is
a) Halved
b) Unchanged
c) Doubled
d) Increased by factor \[\sqrt{2}\]
Explanation: The average K.E. of helium atoms is doubled
35. The time average of the kinetic energy of one molecule of a gas taken over a long period of time
a) Is proportional to the square root of the absolute temperature of the gas
b) Is proportional to the absolute temperature of the gas
c) Is proportional to the square of the absolute temperature of the gas
d) Does not depend upon the absolute temperature of the gas
Explanation: The time average of the kinetic energy of one molecule of a gas taken over a long period of time is proportional to the absolute temperature of the gas
36. The kinetic energy per gm mol for a diatomic gas at room temperature is
a) 3 RT
b) \[\frac{5}{2}RT\]
c) \[\frac{3}{2}RT\]
d) \[\frac{1}{2}RT\]
Explanation: The kinetic energy per gm mol for a diatomic gas at room temperature is \[\frac{5}{2}RT\]
37. At which of the following temperature would the molecules of a gas have twice the average kinetic
energy they have at 20°C
a) 40°C
b) 80°C
c) 313°C
d) 586°C
Explanation:
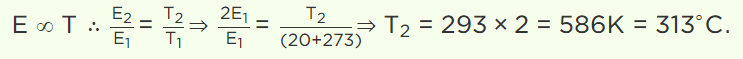
38. The kinetic energy of translation of 20 gm of oxygen at 47°C is (molecular wt. of oxygen is 32 gm/mol and R = 8.3 J/mol/K)
a) 2490 joules
b) 2490 ergs
c) 830 joules
d) 124.5 joules
Explanation:
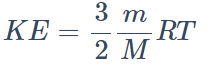
39. The kinetic energy of one gram molecule of a gas at normal temperature and pressure
is (R = 8.31 J /mole - K)
a) \[0.56\times 10^{4} J\]
b) \[1.3\times 10^{2} J\]
c) \[2.7\times 10^{2} J\]
d) \[3.4\times 10^{3} J\]
Explanation:
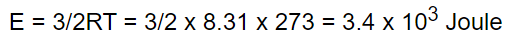
40. The mean kinetic energy of a gas at 300 K is 100 J. The mean energy of the gas at 450 K is equal to
a) 100 J
b) 3000 J
c) 450 J
d) 150 J
Explanation:
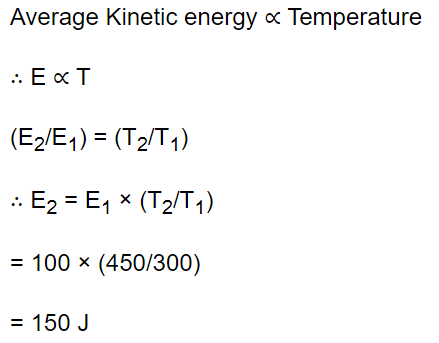
41. At what temperature is the kinetic energy of a gas molecule double that of its value of 27°C
a) 54°C
b) 300 K
c) 327°C
d) 108°C
Explanation:

42. Read the given statements and decide which is/are correct on the basis of kinetic theory of gases
(I) Energy of one molecule at absolute temperature is zero
(II) r.m.s. speeds of different gases are same at same temperature
(III) For one gram of all ideal gas kinetic energy is same at same temperature
(IV) For one mole of all ideal gases mean kinetic energy is same at same temperature
a) All are correct
b) I and IV are correct
c) IV is correct
d) None of these
Explanation: None of these
43. The translational kinetic energy of gas molecule for one mole of the gas is equal to
a) \[\frac{3}{2}RT\]
b) \[\frac{2}{3}RT\]
c) \[\frac{1}{2}RT\]
d) \[\frac{2}{3}KT\]
Explanation: The translational kinetic energy of gas molecule for one mole of the gas is equal to \[\frac{3}{2}RT\]
44. At 27°C temperature, the kinetic energy of an ideal gas is E1 . If the temperature is increased to
327°C, then kinetic energy would be
a) \[2E_{1}\]
b) \[\frac{1}{2}E_{1}\]
c) \[\sqrt{2}E_{1}\]
d) \[\frac{1}{\sqrt{2}}E_{1}\]
Explanation:
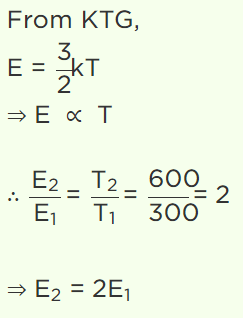
45. The average kinetic energy of a gas molecule at 27°C is \[6.21\times 10^{-21}J\] . Its average kinetic energy at
227°C will be
a) \[52.2\times 10^{-21}J\]
b) \[5.22\times 10^{-21}J\]
c) \[10.35\times 10^{-21}J\]
d) \[11.35\times 10^{-21}J\]
Explanation:
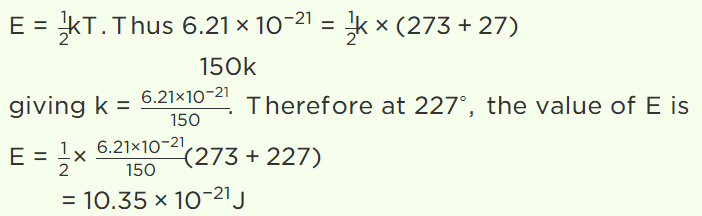
46. The average translational kinetic energy of \[O_{2}\] (molar mass 32) molecules at a particular temperature is 0.048 eV. The translational kinetic
energy of \[N_{2}\] (molar mass 28) molecules in eV at the same temperature is
a) 0.0015
b) 0.003
c) 0.048
d) 0.768
Explanation: 0.048
47. The average translational energy and the r.m.s. speed of molecules in a sample of oxygen gas at 300 K are \[6.21\times 10^{-21}J\] and 484 m/s respectively.
The corresponding values at 600 K are nearly (assuming ideal gas behaviour)
a) \[12.42\times 10^{-21}J\] ,968 m / s
b) \[8.78\times 10^{-21}J\] ,684 m / s
c) \[6.21\times 10^{-21}J\] ,968 m / s
d) \[12.42\times 10^{-21}J\] ,684 m / s
Explanation:

48. A polyatomic gas with n degrees of freedom has a mean energy per molecule given by
a) \[\frac{nkT}{N}\]
b) \[\frac{nkT}{2N}\]
c) \[\frac{nkT}{2}\]
d) \[\frac{3kT}{2}\]
Explanation: A polyatomic gas with n degrees of freedom has a mean energy per molecule given by \[\frac{nkT}{2}\]
49. At 0 K which of the following properties of a gas will be zero
a) Kinetic energy
b) Potential energy
c) Vibrational energy
d) Density
Explanation: At 0 K, Kinetic energy of a gas will be zero
50.At the same temperature and pressure and volume of two gases, which of the following quantities is
constant
a) Total number of molecules
b) Average kinetic energy
c) Root mean square velocity
d) Mean free path
Explanation: At the same temperature and pressure and volume of two gases, Average kinetic energy is constant
51. A box contains a mixture of \[H_{2}\] and He gases. Which of the following statements are corrects
a) The average translational kinetic energies of \[H_{2}\] molecules and He atoms are same
b) The average energies of \[H_{2}\] molecules and He atoms are same
c) H2 molecules have greater average energy than that of He atoms
d) Both a and c
Explanation: Both a and c
52. If temperature of gas increases from \[27^{\circ} C\] to \[927^{\circ} C\] the K.E. will be
a) Double
b) Half
c) One fourth
d) Four times
Explanation: If temperature of gas increases from \[27^{\circ} C\] to \[927^{\circ} C\] the K.E. will be Four times
53. Vessel A is filled with hydrogen while vessel B, whose volume is twice that of A, is filled with the same mass of oxygen at the same temperature.
The ratio of the mean kinetic energies of hydrogen and oxygen is
a) 16 : 1
b) 1 : 8
c) 8 : 1
d) 1 : 1
Explanation: Vessel A is filled with hydrogen while vessel B, whose volume is twice that of A, is filled with the same mass of oxygen at the same temperature. The ratio of the mean kinetic energies of hydrogen and oxygen is 1 : 1
54. Energy of all molecules of a monoatomic gas having a volume V and pressure P is \[\frac{3}{2}PV\] . The total translational kinetic energy of all molecules of a diatomic gas as the same volume and pressure is
a) \[\frac{1}{2}PV\]
b) \[\frac{3}{2}PV\]
c) \[\frac{5}{2}PV\]
d) 3PV
Explanation: \[\frac{3}{2}PV\]
55. On absolute temperature, the kinetic energy of the molecules
a) Becomes zero
b) Becomes maximum
c) Becomes minimum
d) Remains constant
Explanation: On absolute temperature, the kinetic energy of the molecules becomes zero
56. The temperature of a gas is \[-68^{\circ} C\] . At what temperature will the average kinetic energy of its molecules be twice that of at \[-68^{\circ} C\]
a) \[137^{\circ} C\]
b) \[127^{\circ} C\]
c) \[100^{\circ} C\]
d) \[105^{\circ} C\]
Explanation: \[137^{\circ} C\]
57. The average kinetic energy of a helium atom at \[30^{\circ} C\] is
a) Less than 1 eV
b) A few keV
c) 50-60 eV
d) 13.6 eV
Explanation: The average kinetic energy of a helium atom at \[30^{\circ} C\] is less than 1 eV
58. Two gases are at absolute temperatures 300 K and 350 K respectively. Ratio of average kinetic energy of their molecules is
a) 7 : 6
b) 6 : 7
c) 36 : 49
d) 49 : 36
Explanation: Two gases are at absolute temperatures 300 K and 350 K respectively. Ratio of average kinetic energy of their molecules is 6 : 7
59. A gas mixture consists of molecules of type 1, 2 and 3, with molar masses \[m_{1}>m_{2}>m_{3}\] . \[V_{rms}\] and \[\bar{K}\] are the r.m.s. speed and average kinetic energy of the gases. Which of the following is true
a) \[\left(V_{rms}\right)_{1}<\left(V_{rms}\right)_{2}<\left(V_{rms}\right)_{3}\] and \[\left(\bar{K}\right)_{1}=\left(\bar{K}\right)_{2}=\left(\bar{K}\right)_{3}\]
b) \[\left(V_{rms}\right)_{1}=\left(V_{rms}\right)_{2}=\left(V_{rms}\right)_{3}\] and \[\left(\bar{K}\right)_{1}=\left(\bar{K}\right)_{2}>\left(\bar{K}\right)_{3}\]
c) \[\left(V_{rms}\right)_{1}>\left(V_{rms}\right)_{2}>\left(V_{rms}\right)_{3}\] and \[\left(\bar{K}\right)_{1}<\left(\bar{K}\right)_{2}>\left(\bar{K}\right)_{3}\]
d) \[\left(V_{rms}\right)_{1}>\left(V_{rms}\right)_{2}>\left(V_{rms}\right)_{3}\] and \[\left(\bar{K}\right)_{1}<\left(\bar{K}\right)_{2}<\left(\bar{K}\right)_{3}\]
Explanation: \[\left(V_{rms}\right)_{1}<\left(V_{rms}\right)_{2}<\left(V_{rms}\right)_{3}\] and \[\left(\bar{K}\right)_{1}=\left(\bar{K}\right)_{2}=\left(\bar{K}\right)_{3}\]
60. On colliding in a closed container the gas molecules
a) Transfer momentum to the walls
b) Momentum becomes zero
c) Move in opposite directions
d) Perform Brownian motion
Explanation: On colliding in a closed container the gas molecules transfer momentum to the walls