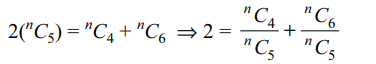PrepBharat

1. Consider all 2ⁿ – 1 non-empty subsets of the set{1, 2, 3, .... n } product of each of its elements. Sum of all these products is
a) (n + 1)!
b) (n + 1)! + 1
c) (n + 1)! – 1
d) n! – 2

View Answer

2. Consider all \[2^{n}-1\]  non-empty subsets of the set {1, 2, .... , n} . For every such subset we find the product of reciprocals of each of its elements. Sum of all these products is
a) n
b) n + 1
c) n!
d) n!-1

View Answer

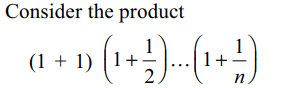
3. The number of ways in which we can arrange 4 letters of the word MATHEMATICS is given by
a) 136
b) 2454
c) 1680
d) 192

View Answer

4. The number of ways in which we can distribute mn students equally among m sections is given by
a) \[\frac{\left(mn\right)!}{n!}\]
b) \[\frac{\left(mn\right)!}{\left(n!\right)^{m}}\]
c) \[\frac{\left(mn\right)!}{m!n!}\]
d) \[\left(mn\right)^{m}\]

View Answer

5. If a polygon has 90 diagonals, the number of its sides is given by
a) 12
b) 11
c) 10
d) 15

View Answer

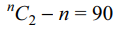
6. Out of 10 white, 8 black and 6 red balls, the number of ways in which one or more balls can be selected is given by
a) 681
b) 691
c) 679
d) 692

View Answer

7. A is a set containing n elements. A subset P of A is chosen. The set A is reconstructed by replacing the elements of P. A subset Q of A is again chosen. The number of ways of choosing P and Q so that \[ P\cap Q \]   contains exactly two elements is
a) \[9\times ^{n}C_{2}\]
b) \[3^{n}- ^{n}C_{2}\]
c) \[2\times ^{n}C_{n}\]
d) \[ ^{n}C_{2}.3^{n-2}\]

View Answer

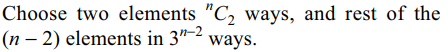
8. Ten different letters of an alphabet are given. Words with five letters are formed from these given letters . The number of words which have at least one of their letters repeated is
a) 69760
b) 30240
c) 99748
d) 60480

View Answer

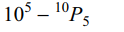
9. The number of ways in which we can select four numbers from 1 to 30 so as to exclude every selection of four consecutive numbers is
a) 27378
b) 27405
c) 27397
d) 19050

View Answer

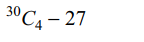
10. If \[ ^{n}C_{4}\] , \[ ^{n}C_{5}\] and \[ ^{n}C_{6}\] are in A.P., the value of n can be
a) 14
b) 11
c) 9
d) 5

View Answer