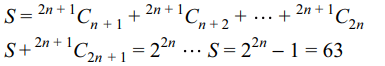1.Let \[E=\left[\frac{1}{3}+\frac{1}{50}\right]+\left[\frac{1}{3}+\frac{2}{50}\right]+....\] upto 50 terms, then
a) E is divisible by exactly 2 primes
b) E is prime
c) \[E\leq 35\]
d) Both b and c
Explanation:
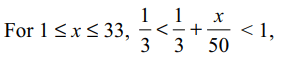
2. If n < p < 2n and p is prime and \[N=^{2n}C_{n}\] , then
a) \[p\mid N\]
b) \[p^{4}\mid N\]
c) \[p^{2}\mid N\]
d) \[p^{3}\mid N\]
Explanation: n! N = (n + 1) (n + 2) .... (2n)
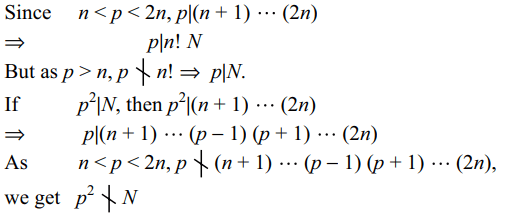
3. A is a set containing n elements. A subset
\[P_{1}\] of A is chosen. The set A is reconstructed by replacing
the elements of \[P_{1}\] . Next a subset \[P_{2}\] of A is chosen and
again the set is reconstructed by replacing the elements
of \[P_{2}\] . In this way m(> 1) subsets \[P_{1},P_{2},....P_{m}\] of A are
chosen. The number of ways of choosing \[P_{1},P_{2},....P_{m}\] so
that \[P_{i}\cap P_{j}=\phi\] for \[ i\neq j\] , is
a) \[\left(m+1\right)^{n}\]
b) \[2^{m}- ^{m}C_{n}\]
c) \[ \sum_{k=0}^{n}.^{m}C_{k}m^{k}\]
d) Both a and c
Explanation: Let the set A be {a1, a2, .... , an}. In the first case,
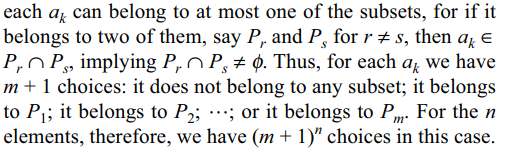
4. With \[P_{1},P_{2},....P_{m}\] as in Q3,
the number of ways of choosing \[P_{1},....P_{m}\] so that
\[P_{1}\cap P_{2}\cap....\cap P_{m}=\phi\] is
a) \[\left(2^{m}-1\right)^{n}\]
b) \[\left(1+2+....+2^{m-1}\right)^{n}\]
c) \[\left(m+1\right)^{n}\]
d) Both a and b
Explanation:
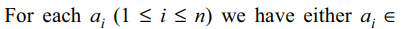
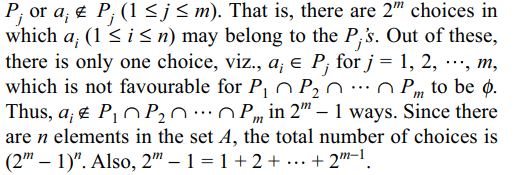
5. The number of 10 digit numbers that can be formed
by using the digits 2 and 3 is
a) \[^{10}C_{2}+^{9}C_{2}\]
b) \[2^{10}\]
c) \[2^{10}-2\]
d) 10!
Explanation: For each place we have two choices
6. If \[P_{r}\] stands for \[^{r}P_{r}\] , then sum of the series \[1+P_{1}+2P_{2}+3P_{3}+....+nP_{n}\] is
a) \[P_{n+1}\]
b) \[P_{n+1}-1\]
c) \[P_{n+1}+1\]
d) none of these
Explanation:
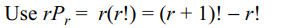
7. If \[a_{n}=\sum_{r=0}^{n}\frac{1}{^{n}C_{r}}\] then value of\[\sum_{r=0}^{n}\frac{n-2r}{^{n}C_{r}}\] is
a) \[\frac{n}{2}a_{n}\]
b) \[\frac{1}{4}a_{n}\]
c) \[na_{n}\]
d) 0
Explanation:
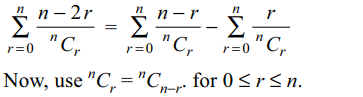
8. m men and w women are to be seated in a row so
that all men sit together. The number of ways in
which they can be seated is
a) (w + 1)! m!
b) m! w!
c) m! (w – 1)!
d) \[^{n}C_{w}\]
Explanation: First treat m men as just one object. We can permute (w + 1) objects in (w + 1)! and the m men is m! ways.
9. A five digit number divisible by 6 is to be formed by using the digits 0, 1, 2, 3, 4 and 8 without repetition.The total number of ways in which this can be done
is
a) 216
b) 150
c) 116
d) 98
Explanation: Use sum of digits must be divisible by 3 and the last digit should be an even number.
10. Rakshit is allowed to select (n + 1) or more books
out of (2n +1) distinct books. If the number of ways
in which he may not select all of them is 63, then
value of n is
a) 3
b) 4
c) 5
d) 11
Explanation: