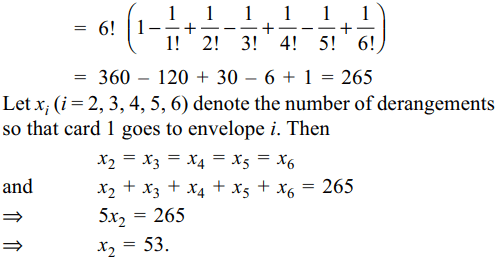1. Sum of all three digit numbers (no digit
being zero) having the property that all digits are perfect
squares, is
a) 3108
b) 6216
c) 13986
d) 310
Explanation: The non-zero perfect square digits are 1, 4 and 9.
1 can occur at units place in 3 × 3 = 9 ways.
Sum due to 1 at unit’s place is 1 × 9. Similarly, sum due to 1 at ten’s place is 1 × 10 × 9 and sum due to 1 at hundred’s place is 1 × 100 × 9. We can deal with the digits 4 and 9 in a similar way.
Thus, sum of the desired number is
(1 + 4 + 9) (1 + 10 + 100) (9) = 13986
2. The number of ordered pairs \[\left(m,n\right),m,n \epsilon \left\{1,2,....,100\right\}\] such that \[7^{m}+7^{n}\] is divisible by 5 is
a) 1250
b) 2000
c) 2500
d) 5000
Explanation: Note that 7r (r ∈ N) ends in 7, 9, 3 or 1 (corresponding to r = 1, 2, 3 and 4 respectively).

3. The greatest value of \[^{2n}C_{r}\left(0\leq r\leq2n\right)\] is
a) \[^{2n}C_{n-1}\]
b) \[^{2n}C_{n+1}\]
c) \[^{2n}C_{n}\]
d) \[^{2n}C_{n-2}\]
Explanation:
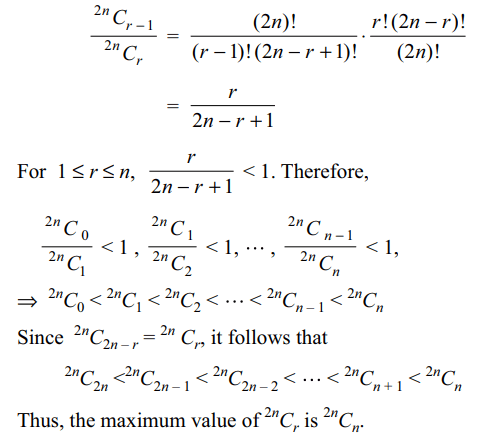
4. Let \[a=\sum_{i< j}\left(\frac{1}{^{n}C_{i}}+\frac{1}{^{n}C_{j}}\right)\] and
\[b=\sum_{i< j}\left(\frac{i}{^{n}C_{i}}+\frac{j}{^{n}C_{j}}\right)\] , then
a) \[b=\left(n-1\right)a\]
b) \[b=\left(n+1\right)a\]
c) \[b=\frac{n}{2}a\]
d) \[b=n-a\]
Explanation:
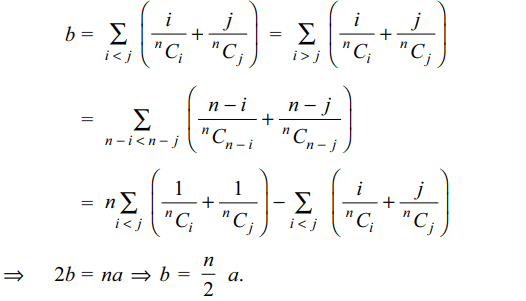
5. Let S = {1, 2, 3, .... , n}. If X denote the set
of all subsets of S containing exactly two elements, then the
value of \[\sum_{A \epsilon X}\] (min A) is
a) \[^{n+1}C_{3}\]
b) \[^{n}C_{3}\]
c) \[^{n}C_{2}\]
d) \[^{n+1}C_{4}\]
Explanation: There are exactly (n – 1) subsets of S containing two elements having 1 as least element; exactly (n – 2) subsets of S having 2 as least element and so on. Thus,
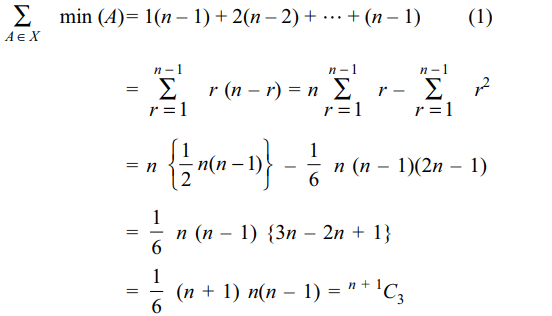
6. Let 'a' be a factor of 120, then the number
of positive integral solutions of \[x_{1}x_{2}x_{3}=a\] is
a) 160
b) 320
c) 480
d) 960
Explanation: Let x4 be such that x4 = 120/a. Then, the

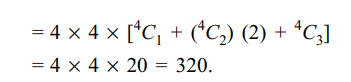
7. The value of \[n\epsilon N\] for which
\[^{m}C_{2}=210\]
where \[m=^{n}C_{2}\] is
a) 4
b) 5
c) 6
d) 7
Explanation:
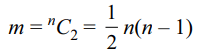
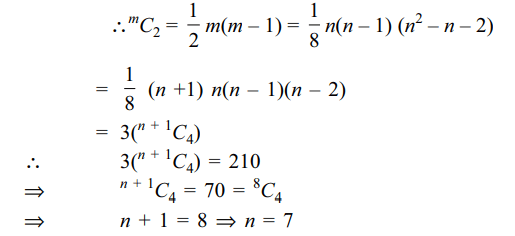
8. A committee consisting of at least three
members is to be formed from a group of 6 boys and 6 girls
such that it always has a boy and a girl. The number of
ways to form such committee is:
a) \[2^{12}-2^{7}-13\]
b) \[2^{11}-2^{6}-13\]
c) \[2^{12}-2^{7}-35\]
d) \[2^{11}-2^{7}-35\]
Explanation:
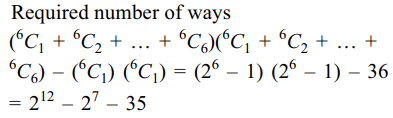
9. The total number of ways in which 5 balls
of different colours can be distributed among 3 persons so
that each person gets at least one ball is
a) 75
b) 150
c) 210
d) 243
Explanation: 5 balls can be distributed to 3 persons by giving (2, 2, 1) balls or by (3, 1, 1) balls. Each of the above distribution has three such ways.
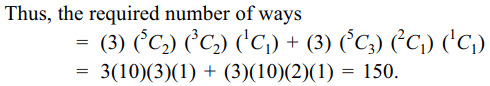
10. Six cards and six envelopes are numbers
1, 2, 3, 4, 5, 6 and cards are to be placed in envelopes so
that each envelope contains exactly one card and no card
is placed in the envelope bearing the same number and
moreover the card numbered 1 is always placed in envelope
numbered 2. Then the number of ways it can be done is
a) 264
b) 265
c) 53
d) 67
Explanation: Number of derangements