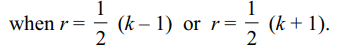1. Let an, bn, \[n\epsilon N\] be defined as follows :
\[a_{1}=1,a_{1}+2a_{2}+....+na_{n}=a_{n+1}\forall n\geq 1\]
and \[b_{1}=1,b_{1}+\frac{1}{2}b_{2}+....+\frac{1}{n}b_{n}=b_{n+1}\forall n\geq 2\] , then
a) \[a_{n}=\frac{1}{2}\left(n!\right)\forall n\geq 2\]
b) \[b_{n}=\frac{1}{2}n\forall n\geq 2\]
c) \[\sum_{k=1}^{n}a_{k}b_{k}=\frac{1}{4}\left(\left(n+1\right)!+2\right)\]
d) All of the above
Explanation: For n ≥ 1,
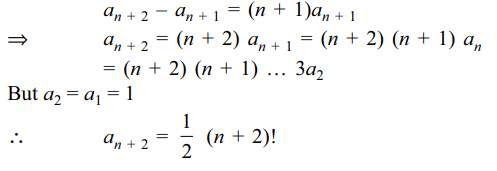
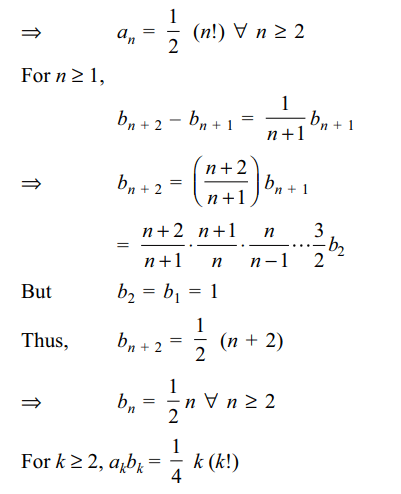
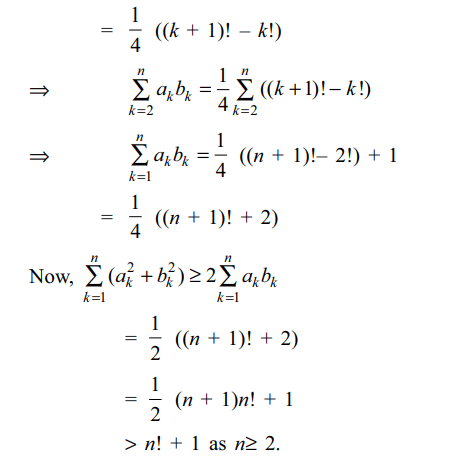
2. A class has 30 students. The following
prizes are to be awarded to the students of this class. First
and second in Mathematics; first and second in Physics first
in Chemistry and first in Biology. If N denote the number
of ways in which this can be done, then
a) \[400\mid N\]
b) \[600\mid N\]
c) \[8100\mid N\]
d) All of the above
Explanation: First and second prizes in Mathematics (Physics) can be awarded in \[^{30}P_{2}\] ( \[^{30}P_{2}\] ) ways. First prize

3. A letter lock consists of three rings
marked with 15 different letters. If N denotes the number of
ways in which it is possible to make unsuccessful attempts
to open the lock, then
a) \[482\mid N\]
b) N is product of 2 distinct prime numbers
c) N is product of 3 distinct prime numbers
d) Both a and c
Explanation: Since each ring has 15 positions, the total number of attempts that can be made to open the lock is 153 . Out of these, there is just one attempt in which the lock will open. Therefore,
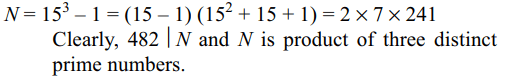
4. \[^{2n}P_{n}\] is equal to
a) (n + 1) (n + 2).... (2n)
b) \[2^{n}\left[1.3.5 .... \left(2n-1\right)\right]\]
c) (2) . (6) . (10).... (4n – 2)
d) All of the above
Explanation:
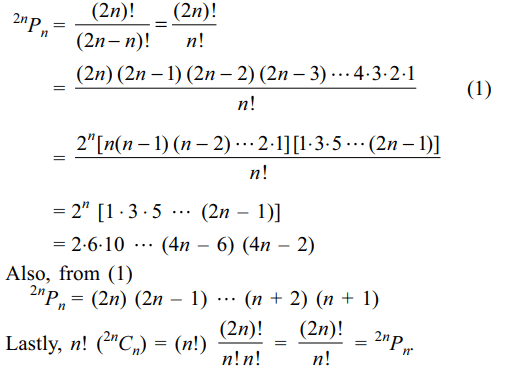
5.If n objects are arranged in a row, then the
number of ways of selecting three of these objects so that
no two of them are next to each other is
a) \[\frac{1}{6}\left(n-2\right)\left(n-3\right)\left(n-4\right)\]
b) \[^{n-2}C_{3}\]
c) \[^{n-3}C_{3}+^{n-3}C_{2}\]
d) All of the above
Explanation: Let x0 be the number of objects to the left of the

6.The number of non-negative integral
solutions of \[x_{1}+x_{2}+x_{3}+x_{4}\leq n\] (where n is a positive
integer) is
a) \[^{n+3}C_{3}\]
b) \[^{n+4}C_{4}\]
c) \[^{n+4}C_{n}\]
d) Both b and c
Explanation: Let x5 be such that x1 + x2 + x3 + x4 + x5 = n. We now seek the non-negative integral solutions of x1 + x2 + x3 + x4 + x5 = n. The number of required solutions = \[^{n+4}C_{n}\] = \[^{n+4}C_{4}\]
7. The number of ways of choosing triplets
(x, y, z) such that z ≥ max {x, y} and \[x,y,z \epsilon \left\{1,2,....,n,n+1\right\}\] is
a) \[^{n+1}C_{3}+^{n+2}C_{3}\]
b) \[\frac{1}{6}n\left(n+1\right) \left(2n +1\right)\]
c) \[1^{2}+2^{2}+....+n^{2}\]
d) All of the above
Explanation: When z = n + 1, we can choose x, y from
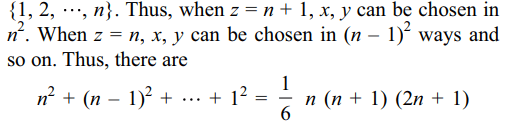
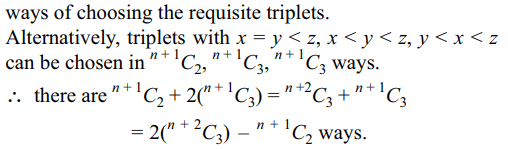
8. If \[100!=2^{\alpha}3^{\beta}5^{\gamma}7^{\delta}....\] , then
a) \[\alpha=97\]
b) \[\beta=\frac{1}{2}\left(\alpha-1\right)\]
c) \[\gamma=\frac{1}{2}\beta\]
d) All of the above
Explanation:
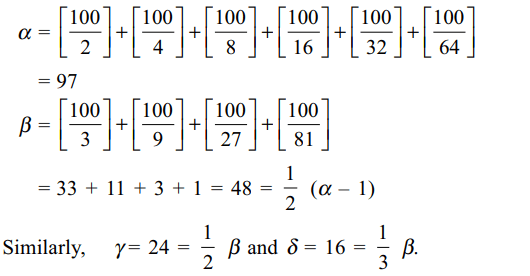
9. The number of triangles that can be
formed with the sides of lengths a, b and c where a, b, c
are integers such that \[a\leq b\leq c\] is
a) \[\frac{1}{4}\left(c+1\right)^{2}\] when c is odd
b) \[\frac{1}{2}c\left(c+1\right)\] when c is odd
c) \[\frac{1}{4}c\left(c+2\right)\] when c is even
d) Both a and c
Explanation: Let c = 2m + 1 where m is a positive integer.
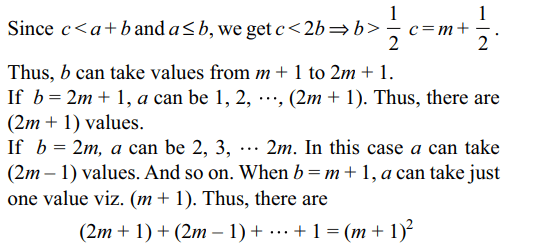
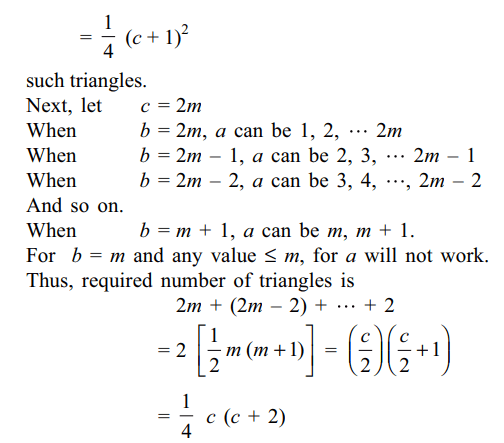
10. If k is odd then \[^{k}C_{r}\] is maximum for r
equal to
a) \[\frac{1}{2}\left(k-1\right)\]
b) \[\frac{1}{2}\left(k+1\right)\]
c) k-1
d) Both a and b
Explanation: Let k = 2n + 1, then \[^{2n+1}C_{r}\] is maximum when r = n. Also \[^{2n+1}C_{n}\] = \[^{2n+1}C_{n+1}\]. Thus, \[^{k}C_{r}\] is maximum