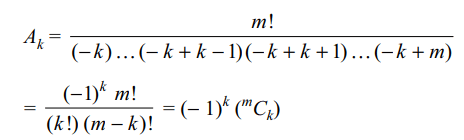1. The number of ways in which a committee of 3
women and 4 men be chosen from 8 women and 7
men if Ms. X refuses to serve on the committee if
Mr. Y is a member of the committee is
a) 420
b) 840
c) 1540
d) 720
Explanation:
2. The product of first n odd natural numbers equals
a) \[\left(^{2n}C_{n}\right)\left(^{n}P_{n}\right)\]
b) \[\left(\frac{1}{2}\right)^{n}\left(^{2n}C_{n}\right)\left(^{n}P_{n}\right)\]
c) \[\left(\frac{1}{4}\right)\left(^{2n}C_{n}\right)\left(^{2n}P_{n}\right)\]
d) \[\left(\frac{1}{n!}\right)\left(^{2n}C_{n}\right)\]
Explanation:
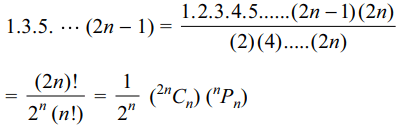
3. The number of integral solutions of x + y + z = 0
with x ≥ – 5, y ≥ – 5, z ≥ – 5 is
a) 134
b) 136
c) 138
d) 140
Explanation:
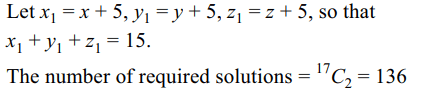
4. A library has n different books and has p copies of
each of the book. The number of ways of selecting
one or more books from the library is
a) \[n^{p}\]
b) \[p^{n}\]
c) \[\left(n+1\right)^{p}-1\]
d) \[\left(p+1\right)^{n}-1\]
Explanation: For each book we have (p + 1) choices.
5. The number of ways in which we can get a score of
11 by throwing three dice is
a) 18
b) 27
c) 45
d) 56
Explanation:
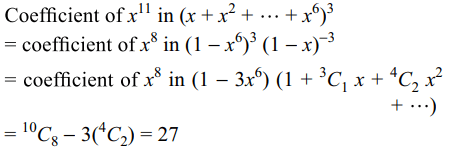
6. 2m white counters and 2n red counters are arranged
in a straight line with (m + n) counters on each
side of a central mark. The number of ways of
arranging the counters, so that the arrangements are
symmetrical with respect to the central mark, is
a) \[^{m+n}C_{m}\]
b) \[^{2m+2n}C_{2m}\]
c) \[\frac{1}{2}\frac{\left(m+n\right)!}{m!n!}\]
d) mn
Explanation: Arrange m white and n red counters on one side of the central mark.
7. Let x = (2n + 1) (2n + 3) …. (4n – 3) (4n – 1) and \[y=\left(\frac{1}{2}\right)^{n}\frac{\left(4n\right)!n!}{\left(2n\right)!\left(2n\right)!}\]
then \[x-y+2^{n}\] is equal to
a) 0
b) \[\left(2n\right)!/2^{n}\]
c) \[^{2n}C_{n}\]
d) \[2^{n}\]
Explanation:
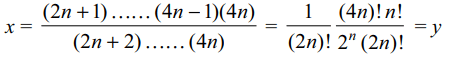
8. There are 3 set of parallel lines containing
respectively p lines, q lines and r lines respectively.The greatest number of parallelograms that can be
formed by the system
a) pqr + (p – 1) (q – 1) (r – 1)
b) \[\frac{1}{4}\left\{pqr+\left(p-1\right)\left( q-1 \right)\left(r-1\right)\right\}\]
c) \[\frac{1}{4}pqr\left(p+1\right)\left( q+1 \right)\left(r+1\right)\]
d) \[\left(^{p}C_{2}\right)\left( ^{q}C_{2} \right)+\left(^{q}C_{2}\right)\left(^{r}C_{2}\right)+\left(^{r}C_{2}\right)\left(^{p}C_{2}\right)\]
Explanation:
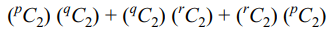
9.The number of six-digit numbers which have sum
of their digits as an odd integer, is
a) 45000
b) 450000
c) 97000
d) 970000
Explanation: For the first time we have nine choice, for each of the next four 10 choices. At this stage add the numbers already written and the choose digit for the unit’s place is 5 ways.
10. In the identity
\[\frac{m!}{x \left(x+1\right) \left(x+2\right) ....\left(x+m\right)}=\sum_{i=0}^{m}\frac{A_{i}}{x+i}\] ,
then value of \[A_{k}\] is
a) \[^{m}C_{k}\]
b) \[^{m}C_{k+1}\]
c) \[\left(-1\right)^{k}\left(^{m}C_{k}\right)\]
d) \[^{m}C_{k-1}\]
Explanation: