1. For a satellite moving in an orbit around the earth, the ratio of kinetic energy to potential
energy is
a) 2
b) \[\frac{1}{2}\]
c) \[\frac{1}{\sqrt{2}}\]
d) \[\sqrt{2}\]
Explanation:

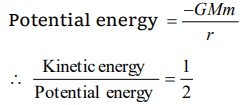
2.The value of escape velocity on a certain planet is 2 km/s. Then the value of orbital speed for a satellite orbiting close to its surface is
a) 12 km/s
b) 1 km/s
c) \[\sqrt{2} km/s\]
d) \[2\sqrt{2} km/s\]
Explanation:
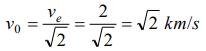
3. Four particles each of mass M, are located at the vertices of a square with side L. The gravitational potential due to this at the centre of the square is
a) \[-\sqrt{32}\frac{GM}{L}\]
b) \[-\sqrt{64}\frac{GM}{L^{2}}\]
c) Zero
d) \[\sqrt{32}\frac{GM}{L}\]
Explanation:
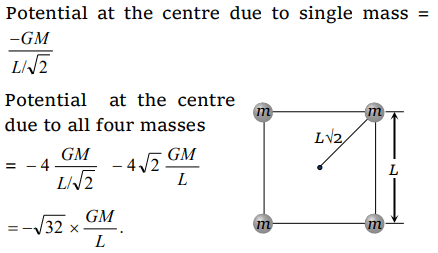
4. There are two planets. The ratio of radius of the two planets is K but ratio of acceleration due to gravity of both planets is g. What will be the ratio of their escape velocity
a) \[\left(kg\right)^{1/2}\]
b) \[\left(kg\right)^{-1/2}\]
c) \[\left(kg\right)^{2}\]
d) \[\left(kg\right)^{-2}\]
Explanation:
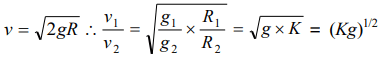
5. Which one of the following statements regarding
artificial satellite of the earth is incorrect
a) The orbital velocity depends on the mass of
the satellite
b) A minimum velocity of 8 km/sec is required by
a satellite to orbit quite close to the earth
c) The period of revolution is large if the radius
of its orbit is large
d) The height of a geostationary satellite is about
36000 km from earth
Explanation: The orbital velocity depends on the mass of the satellite
6. If \[v_{e}\] and \[v_{o}\] represent the escape velocity and orbital velocity of a satellite corresponding to a
circular orbit of radius R, then
a) \[v_{e}=v_{0}\]
b) \[\sqrt{2}v_{o}=v_{e}\]
c) \[v_{e}=v_{0}\diagup\sqrt{2}\]
d) \[v_{e}\] and \[v_{0}\] are not related
Explanation:
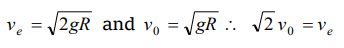
7. If r represents the radius of the orbit of a satellite of mass m moving around a planet of
mass M, the velocity of the satellite is given by
a) \[v^{2}=g\frac{M}{r}\]
b) \[v^{2}=\frac{GMm}{r}\]
c) \[v=\frac{GM}{r}\]
d) \[v^{2}=\frac{GM}{r}\]
Explanation: \[v^{2}=\frac{GM}{r}\]
8. Select the correct statement from the following
a) The orbital velocity of a satellite increases with the radius of the orbit
b) Escape velocity of a particle from the surface
of the earth depends on the speed with which it is fired
c) The time period of a satellite does not depend on the radius of the orbit
d) The orbital velocity is inversely proportional to the square root of the radius of the orbit
Explanation: The orbital velocity is inversely proportional to the square root of the radius of the orbit
9. An earth satellite of mass m revolves in a circular
orbit at a height h from the surface of the earth. R
is the radius of the earth and g is acceleration due
to gravity at the surface of the earth. The velocity
of the satellite in the orbit is given by
a) \[\frac{gR^{2}}{R+h}\]
b) gR
c) \[\frac{gR}{R+h}\]
d) \[\sqrt{\frac{gR^{2}}{R+h}}\]
Explanation:
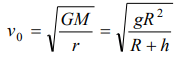
10.Consider a satellite going round the earth in an
orbit. Which of the following statements is wrong
a) It is a freely falling body
b) It suffers no acceleration
c) It is moving with a constant speed
d) Its angular momentum remains constant
Explanation: Centripetal acceleration works on it