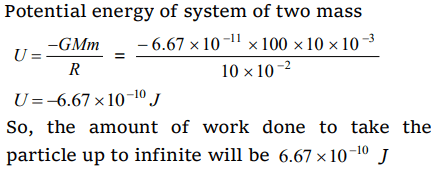1. The escape velocity for the earth is \[v_{e}\] . The escape velocity for a planet whose radius is four times
and density is nine times that of the earth, is
a) \[36v_{e}\]
b) \[12v_{e}\]
c) \[6v_{e}\]
d) \[20v_{e}\]
Explanation:
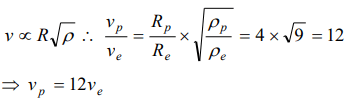
2. The escape velocity for a body projected vertically upwards from the surface of earth is 11 km/s. If the body is projected at an angle of \[45^{\circ}\] with the
vertical, the escape velocity will be
a) \[\frac{11}{\sqrt{2}}km/s\]
b) \[11\sqrt{2}km/s\]
c) 22 km/s
d) 11 km/s
Explanation: Escape velocity does not depends upon the angle of projection.
3. If V, R and g denote respectively the escape velocity from the surface of the earth radius of the earth, and acceleration due to gravity, then
the correct equation is
a) \[v=\sqrt{gR}\]
b) \[v=\sqrt{\frac{4}{3}gR^{3}}\]
c) \[v=R\sqrt{g}\]
d) \[v=\sqrt{2gR}\]
Explanation: \[v=\sqrt{2gR}\]
4. The escape velocity for a body of mass 1 kg from the earth surface is \[11.2 kms^{-1}\] . The escape velocity for a body of mass 100 kg would be
a) \[11.2 \times 10^{2}kms^{-1}\]
b) \[11.2 kms^{-1}\]
c) \[11.2 \times 10^{-2}kms^{-1}\]
d) None of these
Explanation: Escape velocity is independent of mass of object
5.The acceleration due to gravity on a planet is same as that on earth and its radius is four times that of earth. What will be the value of escape
velocity on that planet if it is \[v_{e}\] on earth
a) \[v_{e}\]
b) 2\[v_{e}\]
c) 4\[v_{e}\]
d) \[\frac{v_{e}}{2}\]
Explanation:
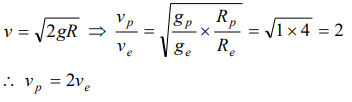
6. If the radius of a planet is four times that of earth and the value of g is same for both, the escape velocity on the planet will be
a) 11.2 km / s
b) 5.6 km / s
c) 22.4 km / s
d) None
Explanation:
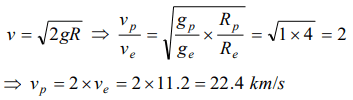
7. If the radius and acceleration due to gravity both are doubled, escape velocity of earth will become
a) 11.2 km/s
b) 22.4 km/s
c) 5.6 km/s
d) 44.8 km/s
Explanation:
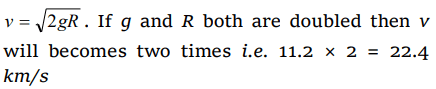
8.A planet has twice the radius but the mean density is\[\frac{1}{4}th\] as compared to earth. What is the ratio of escape velocity from earth to that from
the planet
a) 3 : 1
b) 1 : 2
c) 1 : 1
d) 2 : 1
Explanation:
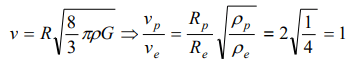
9. The escape velocity from earth is \[v_{es}\] . A body is projected with velocity \[2v_{es}\] with what constant
velocity will it move in the inter planetary space
a) \[v_{es}\]
b) \[3v_{es}\]
c) \[\sqrt{3}v_{es}\]
d) \[\sqrt{5}v_{es}\]
Explanation:
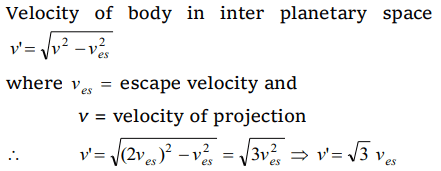
10. A particle of mass 10 g is kept on the surface of a
uniform sphere of mass 100 kg and radius 10 cm.
Find the work to be done against the gravitational
force between them to take the particle far away
from the sphere \[\left(G=6.67\times10^{-11}Nm^{2}\diagup kg^{2}\right)\]
a) \[6.67\times10^{-9}J\]
b) \[6.67\times10^{-10}J\]
c) \[13.34\times10^{-10}J\]
d) \[3.33\times10^{-10}J\]
Explanation: