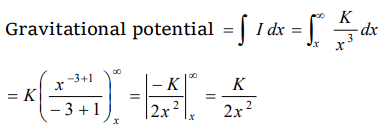1.A body weight 500 N on the surface of the earth. How much would it weigh half way below the surface of the earth
a) 125 N
b) 250 N
c) 500 N
d) 1000 N
Explanation:
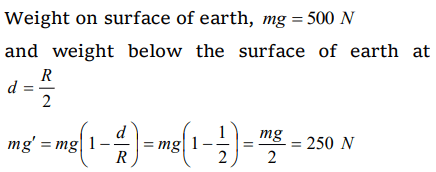
2. If the density of a small planet is the same as that of earth, while the radius of the planet is 0.2 times that of the earth, the gravitational acceleration on the surface of that planet is
a) 0.2 g
b) 0.4 g
c) 2 g
d) 4 g
Explanation:
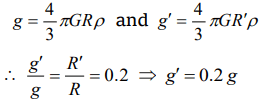
3. Acceleration due to gravity 'g' for a body of mass 'm' on earth's surface is proportional to (Radius of earth=R, mass of earth=M)
a) \[GM\diagup R^{2}\]
b) \[m^{0}\]
c) mM
d) \[1/R^{3/2}\]
Explanation: \[GM\diagup R^{2}\]
4. A body has a weight 90 kg on the earth's surface, the mass of the moon is 1/9 that of the earth's mass and its radius is 1/2 that of the earth's radius. On the moon the weight of the body is
a) 45 kg
b) 202.5 kg
c) 90 kg
d) 40 kg
Explanation:
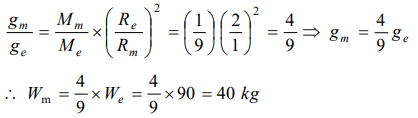
5. The masses of two planets are in the ratio 1 : 2. Their radii are in the ratio 1 : 2. The acceleration due to gravity on the planets are in the ratio
a) 1 : 2
b) 2 : 1
c) 3 : 5
d) 5 : 3
Explanation:
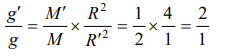
6. If earth is supposed to be a sphere of radius R, if \[g_{30}\] is value of acceleration due to gravity at
latitude of \[30^{\circ}\] and g at the equator, the value of \[g-g_{30^{\circ}}\] is
a) \[\frac{1}{4}\omega^{2}R\]
b) \[\frac{3}{4}\omega^{2}R\]
c) \[\omega^{2}R\]
d) \[\frac{1}{2}\omega^{2}R\]
Explanation:
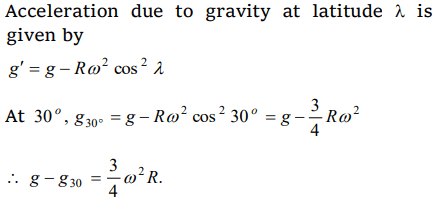
7. If M the mass of the earth and R its radius, the ratio of the gravitational acceleration and the gravitational constant is
a) \[\frac{R^{2}}{M}\]
b) \[\frac{M}{R^{2}}\]
c) \[{MR^{2}}\]
d) \[\frac{M}{R}\]
Explanation:
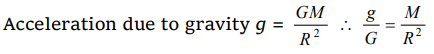
8. A body of mass m rises to height h = R/5 from the earth's surface, where R is earth's radius. If g is acceleration due to gravity at earth's surface, the increase in potential energy is
a) mgh
b) \[\frac{4}{5}mgh\]
c) \[\frac{5}{6}mgh\]
d) \[\frac{6}{7}mgh\]
Explanation:
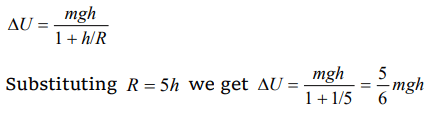
9. In a gravitational field, at a point where the gravitational potential is zero
a) The gravitational field is necessarily zero
b) The gravitational field is not necessarily zero
c) Nothing can be said definitely about the gravitational field
d) None of these
Explanation:
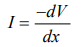
If V = 0 then gravitational field is necessarily zero.
10. The gravitational field due to a mass distribution is \[E=K\diagup x^{3}\] in the x-direction. (K is a constant).
Taking the gravitational potential to be zero at infinity, its value at a distance x is
a) K/x
b) K/2x
c) \[K\diagup x^{2}\]
d) \[K\diagup 2x^{2}\]
Explanation: