1.A body of mass m kg. starts falling from a point 2R above the Earth’s surface. Its kinetic energy when it has fallen to a point ‘R’ above the Earth’s surface [R-Radius of Earth, M-Mass of Earth, G-Gravitational Constant]
a) \[\frac{1}{2}\frac{GMm}{R}\]
b) \[\frac{1}{6}\frac{GMm}{R}\]
c) \[\frac{2}{3}\frac{GMm}{R}\]
d) \[\frac{1}{3}\frac{GMm}{R}\]
Explanation:
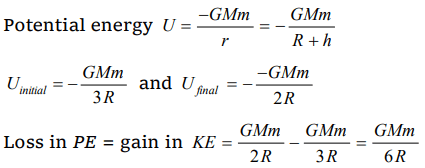
2. A body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to half the escape velocity for that planet.
The maximum height attained by the body is
a) R/3
b) R/2
c) R/4
d) R/5
Explanation:
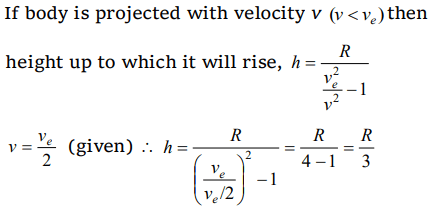
3. Energy required to move a body of mass m from an orbit of radius 2R to 3R is
a) \[GMm\diagup 12R^{2}\]
b) \[GMm\diagup 3R^{2}\]
c) \[GMm\diagup 8R\]
d) \[GMm\diagup 6R\]
Explanation:
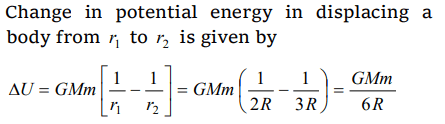
4.The kinetic energy needed to project a body of mass m from the earth surface (radius R) to infinity is
a) mgR/2
b) 2 mgR
c) mgR
d) mgR/4
Explanation:
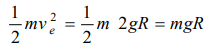
5. Radius of orbit of satellite of earth is R. Its kinetic energy is proportional to
a) \[\frac{1}{R}\]
b) \[\frac{1}{\sqrt{R}}\]
c) R
d) \[\frac{1}{R^{3/2}}\]
Explanation:
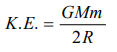
6. In some region, the gravitational field is zero. The gravitational potential in this region
a) Must be variable
b) Must be constant
c) Cannot be zero
d) Must be zero
Explanation:
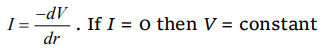
7. A particle falls towards earth from infinity. It’s velocity on reaching the earth would be
a) Infinity
b) \[\sqrt{2gR}\]
c) \[2\sqrt{gR}\]
d) Zero
Explanation:
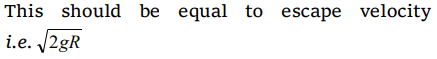
8. Gas escapes from the surface of a planet because it acquires an escape velocity. The escape velocity will depend on which of the following factors :
I. Mass of the planet
II. Mass of the particle escaping
III. Temperature of the planet
IV. Radius of the planet
Select the correct answer from the codes given below :
a) I and II
b) II and IV
c) I and IV
d) I, III and IV
Explanation:
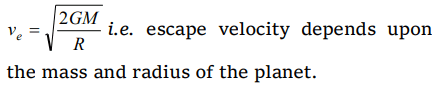
9. \[V_{e}\] and \[V_{p}\] denotes the escape velocity from the earth and another planet having twice the radius and the same mean density as the earth. Then
a) \[V_{e}=V_{p}\]
b) \[V_{e}=V_{p}\diagup 2\]
c) \[V_{e}= 2V_{p}\]
d) \[V_{e}=V_{p}\diagup 4\]
Explanation:
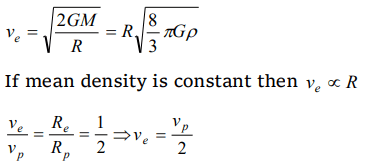
10.The escape velocity of a sphere of mass m from earth having mass M and radius R is given by
a) \[\sqrt{\frac{2GM}{R}}\]
b) 2\[\sqrt{\frac{GM}{R}}\]
c) \[\sqrt{\frac{2GMm}{R}}\]
d) \[\sqrt{\frac{GM}{R}}\]
Explanation: Escape velocity does not depend on the mass of the projectile