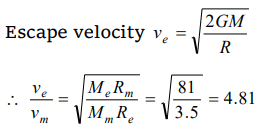1. The escape velocity for a rocket from earth is 11.2 km/sec. Its value on a planet where acceleration due to gravity is double that on the earth and
diameter of the planet is twice that of earth will be in km/sec
a) 11.2
b) 5.6
c) 22.4
d) 53.6
Explanation:
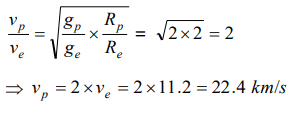
2. The escape velocity from the earth is about 11 km/second. The escape velocity from a planet having twice the radius and the same mean density as the earth, is
a) 22 km/sec
b) 11 km/sec
c) 5.5 km/sec
d) 15.5 km/sec
Explanation:
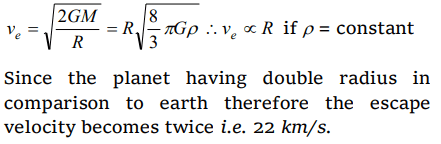
3. A missile is launched with a velocity less than the escape velocity. The sum of its kinetic and potential energy is
a) Positive
b) Negative
c) Zero
d) May be positive or negative depending upon
its initial velocity
Explanation: If missile launched with escape velocity then it will escape from the gravitational field and at infinity its total energy becomes zero. But if the velocity of projection is less than escape velocity then sum of energies will be negative. This shows that attractive force is working on the satellite.
4. If g is the acceleration due to gravity at the earth's surface and r is the radius of the earth, the escape velocity for the body to escape out of earth's gravitational field is
a) gr
b) \[\sqrt{2gr}\]
c) \[g\diagup r\]
d) \[r\diagup g\]
Explanation: \[\sqrt{2gr}\]
5. The escape velocity of a projectile from the earth is approximately
a) 11.2 m/sec
b) 112 km/sec
c) 11.2 km/sec
d) 11200 km/sec
Explanation: 11.2 km/sec
6. The escape velocity of a particle of mass m varies as
a) \[m^{2}\]
b) m
c) \[m^{0}\]
d) \[m^{-1}\]
Explanation: Because it does not depend on the mass of projectile
7. For the moon to cease to remain the earth's satellite, its orbital velocity has to increase by a factor of
a) 2
b) \[\sqrt{2}\]
c) \[1\diagup\sqrt{2}\]
d) \[\sqrt{3}\]
Explanation:

8. The escape velocity of an object from the earth depends upon the mass of the earth (M), its mean density \[\left(\rho\right)\] , its radius (R) and the gravitational
constant (G). Thus the formula for escape velocity
is
a) \[v=R\sqrt{\frac{8\pi}{3}G\rho}\]
b) \[v=M\sqrt{\frac{8\pi}{3}GR}\]
c) \[v=\sqrt{2GMR}\]
d) \[v=\sqrt{\frac{2GM}{R^{2}}}\]
Explanation: \[v=R\sqrt{\frac{8\pi}{3}G\rho}\]
9. Escape velocity on a planet is ve . If radius of the planet remains same and mass becomes 4 times, the escape velocity becomes
a) \[4 v_{e}\]
b) \[2 v_{e}\]
c) \[ v_{e}\]
d) \[\frac{1}{2} v_{e}\]
Explanation:
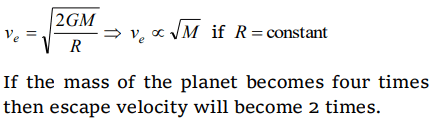
10. The mass of the earth is 81 times that of the moon and the radius of the earth is 3.5 times that of the moon. The ratio of the escape velocity on the surface of earth to that on the surface of moon will be
a) 0.2
b) 2.57
c) 4.81
d) 0.39
Explanation: