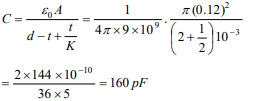1. The area of each plate of a parallel plate capacitor is 100 \[cm^{2}\] and the distance between the plates is 1 mm . It is
filled with mica of dielectric 6. The radius of the equivalent
capacity of the sphere will be
a) 47.7 m
b) 4.77 m
c) 477 m
d) None of the above
Explanation:

2. The respective radii of the two spheres of a spherical
condenser are 12 cm and 9 cm. The dielectric constant of
the medium between them is 6. The capacity of the
condenser will be
a) 240 pF
b) \[240\mu F\]
c) 240 F
d) None of the above
Explanation:
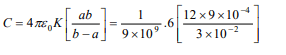
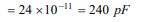
3.A parallel plate condenser is connected with the terminals
of a battery. The distance between the plates is 6 mm . If a
glass plate (dielectric constant K = 9) of 4.5 mm is
introduced between them, then the capacity will become
a) 2 times
b) The same
c) 3 times
d) 4 times
Explanation:
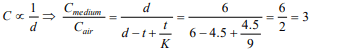
4. The radii of two metallic spheres P and Q are r1 and r2
respectively. They are given the same charge. If \[r_{1}> r_{2}\] .
then on connecting them with a thin wire, the charge will
flow
a) From P to Q
b) From Q to P
c) Neither the charge will flow from P to Q nor from Q to P
d) The information is incomplete
Explanation:

5. A capacitor of capacity C has charge Q and stored energy
is W . If the charge is increased to 2Q , the stored energy
will be
a) 2 W
b) W/ 2
c) 4 W
d) W/ 4
Explanation:

6.Between the plates of a parallel plate condenser, a plate of
thickness \[t_{1}\] and dielectric constant \[k_{1}\] is placed. In the rest
of the space, there is another plate of thickness \[t_{2}\] and
dielectric constant \[k_{2}\] . The potential difference across the
condenser will be
a) \[\frac{Q}{A\epsilon_{0}}\left(\frac{t_{1}}{k_{1}}+\frac{t_{2}}{k_{2}}\right)\]
b) \[\frac{\epsilon_{0}Q}{A}\left(\frac{t_{1}}{k_{1}}+\frac{t_{2}}{k_{2}}\right)\]
c) \[\frac{Q}{A\epsilon_{0}}\left(\frac{k_{1}}{t_{1}}+\frac{k_{2}}{t_{2}}\right)\]
d) \[\frac{\epsilon_{0}Q}{A}\left(k_{1}t_{1}+k_{2}t_{2}\right)\]
Explanation:

7. The distance between the plates of a parallel plate
condenser is 4 mm and potential difference is 60 volts . If
the distance between the plates is increased to 12 mm , then
a) The potential difference of the condenser will become
180 volts
b) The P.D. will become 20 volts
c) The P.D. will remain unchanged
d) The charge on condenser will reduce to one third
Explanation:
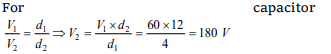
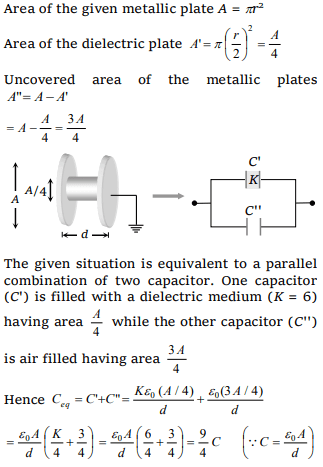
8. The two metallic plates of radius r are placed at a distance
d apart and its capacity is C . If a plate of radius r / 2 and
thickness d of dielectric constant 6 is placed between the
plates of the condenser, then its capacity will be
a) 7C / 2
b) 3C / 7
c) 7C / 3
d) 9C / 4
Explanation:
9. The distance between the plates of a parallel plate
condenser is 8 mm and P.D. 120 volts . If a 6 mm thick slab
of dielectric constant 6 is introduced between its plates,
then
a) The charge on the condenser will be doubled
b) The charge on the condenser will be reduced to half
c) The P.D. across the condenser will be 320 volts
d) The P.D. across the condenser will be 45 volts
Explanation:
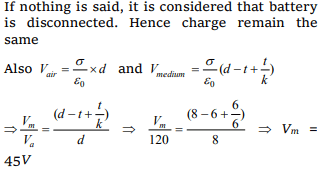
10. In a parallel plate condenser, the radius of each circular
plate is 12 cm and the distance between the plates is 5 mm .
There is a glass slab of 3 mm thick and of radius 12 cm with
dielectric constant 6 between its plates. The capacity of the
condenser will be
a) \[144 \times 10^{-9}F\]
b) 40pF
c) 160 pF
d) \[1.44 \mu F\]
Explanation: