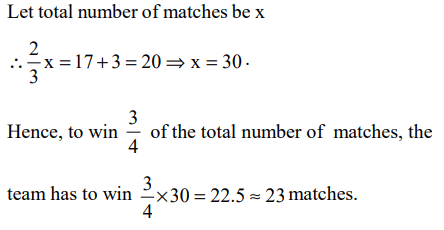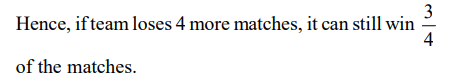1. If a + b + c = 0, where \[a\neq b \neq c \] , then,
\[\frac{a^{2}}{2a^{2}+bc}+\frac{b^{2}}{2b^{2}+ac}+\frac{c^{2}}{2c^{2}+ab}\] is equal to
a) zero
b) 1
c) -1
d) abc
Explanation:
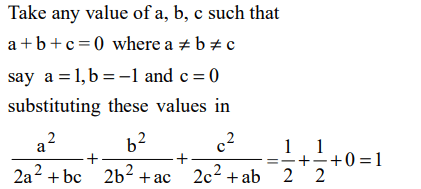
2. If one root of \[x^{2}+px+12=0\] is 4, while the equation \[x^{2}+px+q=0\] has equal roots, then the value of q is
a) 49/4
b) 4/49
c) 4
d) 1/4
Explanation:
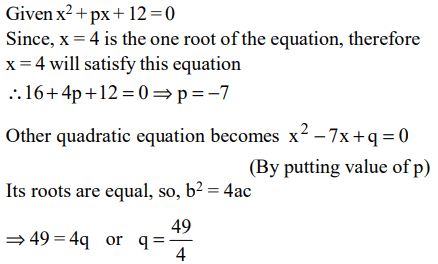
3. Nineteen years from now Jackson will be 3 times as old as Joseph is now. Joseph is three years younger than Jackson.
I. Johnson’s age now
II. Joseph’s age now
a) I > II
b) I < II
c) I = II
d) Nothing can be said
Explanation: Let present age of Jackson be x years and present age of Joseph be y years; then present age of Joseph = x – 3
After 19 years Jackson’s age = (x + 19) years and
Joseph’s age = (y + 19) years.
According to the question:
x + 19 = 3(y + 19)
or x – 3y = 38
So only from above equation x and y cannot be found.
4. What is the value of m which satisfies \[3m^{2}-21m+30\] < 0 ?
a) m < 2 or m > 5
b) m > 2
c) 2 < m < 5
d) m < 5
Explanation:
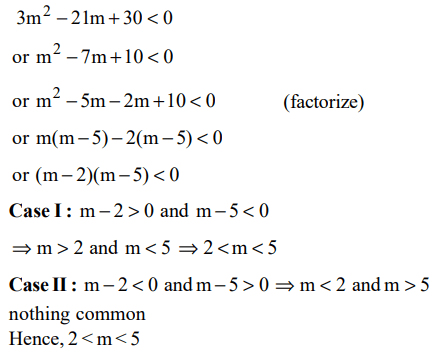
5. The value of \[\frac{55^{3}+45^{3}}{55^{2} - 55\times 45+45^{2}}\] is
a) 100
b) 105
c) 125
d) 75
Explanation:

6. One root of \[x^{2}+kx-8=0\] is square of the other. Then the value of k is
a) 2
b) 8
c) -8
d) -2
Explanation:
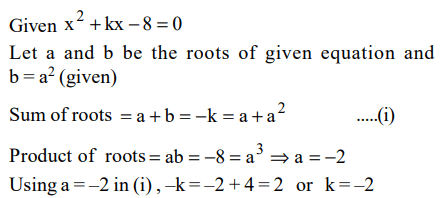
7. Once I had been to the post-office to buy stamps of five rupees, two rupees and one rupee. I paid the clerk Rs 20, and since he
did not have change, he gave me three more stamps of one rupee. If the number of stamps of each type that I had ordered initially
was more than one, what was the total number of stamps that I bought?
a) 10
b) 9
c) 12
d) 8
Explanation: The number of stamps that were initially bought were more than one of each type. Hence, the total number of stamps
= 2(5 rupee) + 2(2 rupee) + 3(1 rupee) + 3(1 rupee)
= 10
8. Given the quadratic equation \[x^{2}-\left(A-3\right)x-\left(A-7\right)\] , for what value of A will the sum of the squares of the roots be zero?
a) -2
b) 3
c) 6
d) None of these
Explanation:

9. Which of the following values of x do not satisfy the inequality \[\left(x^{2}-3x+2>0\right)\] at all?
a) \[1\leq x\leq 2\]
b) \[-1\geq x\geq -2\]
c) \[0\leq x\leq 2\]
d) \[0\geq x\geq -2\]
Explanation:
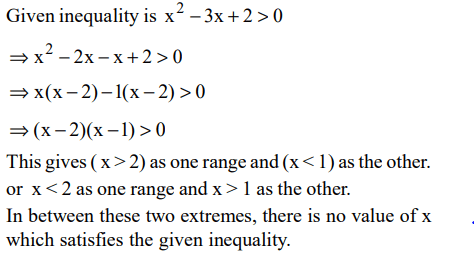
10. Out of two-thirds of the total number of basket-ball matches, a team has won 17 matches and lost 3 of them. what is the maximum
number of matches that the team can lose and still win three-fourths of the total number of matches, if it is true that no match can
end in a tie ?
a) 4
b) 6
c) 5
d) 3
Explanation: