1. The number of roots common between the two equations \[x^{3}+3x^{2}+4x+5=0\]
and \[x^{3}+2x^{2}+7x+3=0\] is
a) 0
b) 1
c) 2
d) 3
Explanation: Subtract the both equations, we get
x2-3x+2 = 0
(x - 1)(x - 2) = 0
x = 1, 2
Roots 1 and 2 do not satisfy any of the original equation.
In case there is a common root, it will be the root of the subtracted equation.
Therefore there is no common root between both the given equations.
2. A real number x satisfying \[1-\frac{1}{n}\] < \[x\leq 3+\frac{1}{n}\]
, for every positive integer n, is best described by
a) 1 < x < 4
b) 1 < \[x\leq3\]
c) 0 < \[x\leq4\]
d) \[1\leq x\leq3\]
Explanation:
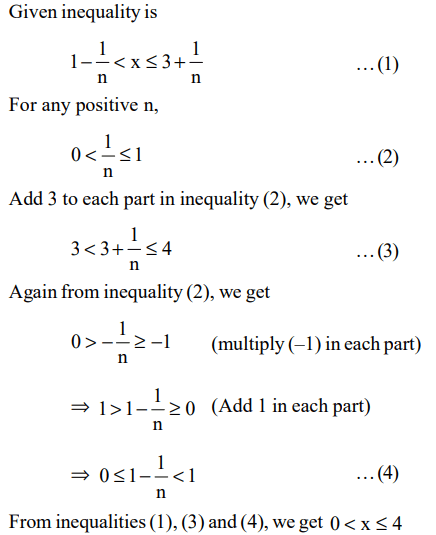
3. If x and y are integers then the equation 5x + 19y = 64 has
a) no solution for x < 300 and y < 0
b) no solution for x > 250 and y > – 100
c) a solution for 250 < x < 300
d) a solution for – 59 < y < – 56
Explanation: 5x + 19y = 64
We see that if y = 1, we get an integer solution x = 9, Now if y changes (increases or decreases) by 5, x will change (decrease or increase) by 19
Looking at options, if x = 256, we get, y = 64
Using these values we see option a, b and d which are eliminated and also that there exists a solution for
250 < x < 300.
4. If both a and b belong to the set {1, 2, 3, 4}, then the number of equations of the form \[a x^{2}+b x+1=0\] having real roots is
a) 10
b) 7
c) 6
d) 12
Explanation:
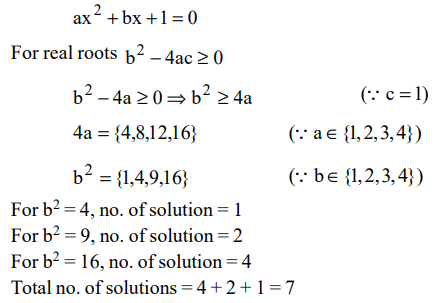
5. If three positive real numbers x, y, z satisfy y – x = z – y and x y z = 4, then what is the minimum possible value of y?
a) \[2^{1/3}\]
b) \[2^{2/3}\]
c) \[2^{1/4}\]
d) \[2^{3/4}\]
Explanation:
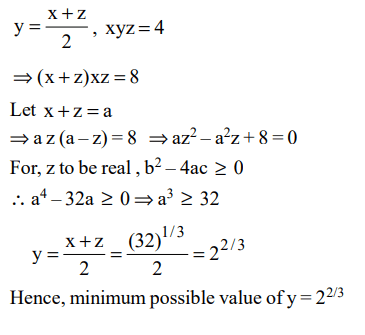
6. If n is such that \[36\leq n\leq72\] , then \[x=\frac{n^{2}+2\sqrt{n}\left(n+4\right)+16}{n+4\sqrt{n+4}}\] satisfies
a) 20 < x < 54
b) 23 < x < 58
c) 25 < x < 64
d) 28 < x < 60
Explanation:
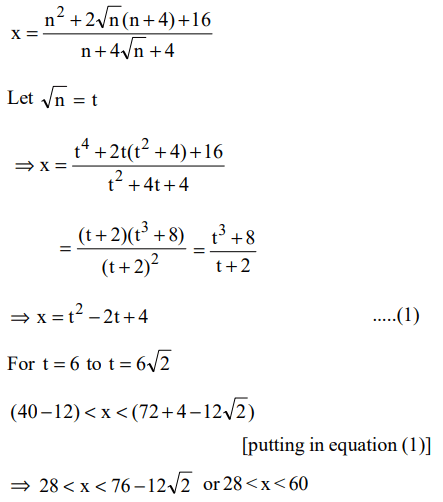
7. If 13x + 1 < 2z and \[z+3=5y^{2}\] , then
a) x is necessarily less than y
b) x is necessarily greater than y
c) x is necessarily equal to y
d) None of the above is necessarily true
Explanation:
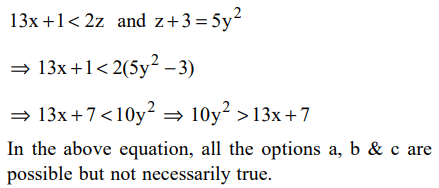
8. If \[\mid b\mid\geq 1\] and \[x=-\mid a \mid b\] , then which one of the following is necessarily true?
a) a – xb < 0
b) \[a-xb\geq 0\]
c) a – xb > 0
d) \[a-xb\leq 0\]
Explanation:
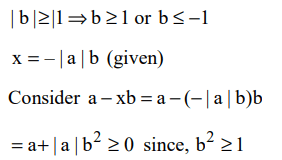
9. The total number of integer pairs (x, y) satisfying the equation x + y = xy is
a) 0
b) 1
c) 2
d) None of the above
Explanation: Equation x + y = xy can be satisfied for (x, y) \[\equiv\] (0, 0), (2, 2)
Hence, total no. of integer pairs (0 and 2) = 2
10. If
\[\frac{a}{b+c}=\frac{b}{c+a}=\frac{c}{a+b}=r\] , then r cannot take any value except
a) \[\frac{1}{2}\]
b) -1
c) \[\frac{1}{2} or -1\]
d) \[-\frac{1}{2} or -1\]
Explanation: There are 2 cases, first, the given condition will be satisfied only when a, b and c are equal and second, when a + b + c = 0. Case (i) : If a = b = c = 1, we get r = 1/2, Case (ii) : when a + b + c = 0, then we get the value of r = – 1. There are no other values that r can take. Hence (c) is the correct option.