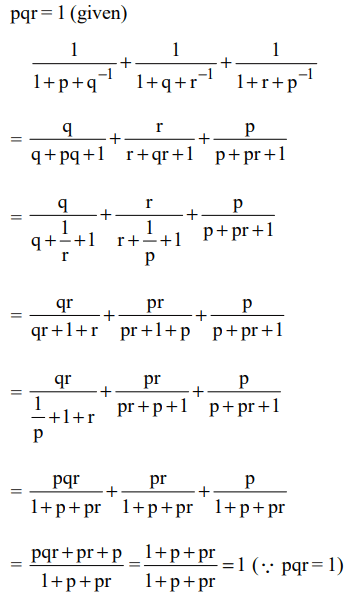1. Two men X and Y started working for a certain company at similar jobs on January 1, 1950. X asked for an initial salary of Rs 300
with an annual increment of Rs 30. Y asked for an initial salary of Rs 200 with a rise of Rs 15 every six months. Assume that the
arrangements remained unaltered till December 31, 1959. Salary is paid on the last day of the month. What is the total amount paid
to them as salary during the period?
a) Rs 93,300
b) Rs 93,200
c) Rs 93,100
d) None of these
Explanation:
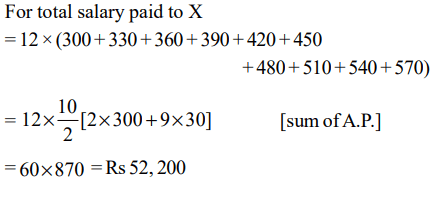
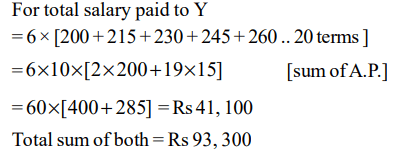
2. x and y are real numbers satisfying the conditions 2 < x < 3 and – 8 < y < – 7. Which of the following expressions will have the least
value?
a) \[x^{2}y\]
b) \[xy^{2}\]
c) 5xy
d) None of these
Explanation:

3. m is the smallest positive integer such that for any integer \[n\leq m\]
, the quantity \[n^{3}-7n^{2}+11n-5\] is positive. What is the value
of m?
a) 4
b) 5
c) 8
d) None of these
Explanation:
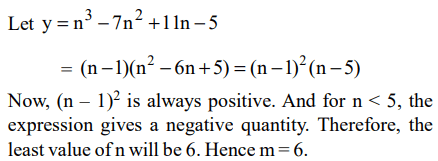
4. Let x, y be two positive numbers such that x + y = 1. Then, the minimum
value of\[\left(x+\frac{1}{x}\right)^{2}+\left(y+\frac{1}{y}\right)^{2}\] is
a) 12
b) 20
c) 12.5
d) 13.3
Explanation:
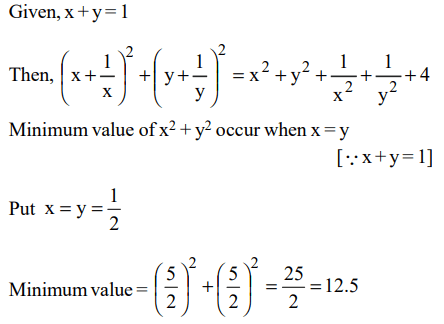
5. Let b be a positive integer and \[a=b^{2} -b\] . If \[b\leq 4\] , then
\[a^{2} -2a\] is divisible by
a) 15
b) 20
c) 24
d) none of these
Explanation:
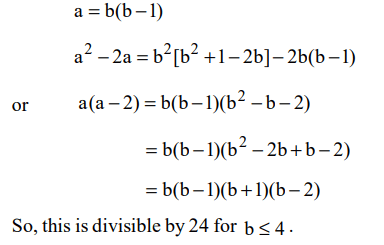
6.Ujakar and Keshab solve a quadratic equation. Ujakar made a mistake in writing down the constant term. He ended up with the
roots (4, 3). Keshab made a mistake in writing down the coefficient of x. He got the roots as (3, 2). What will be the exact roots of
the original quadratic equation?
a) (6, 1)
b) (– 3, – 4)
c) (4, 3)
d) (-4, -3)
Explanation:

7. If x, y and z are real numbers such that, x + y + z = 5 and xy + yz + zx = 3
What is the largest value that x can have?
a) 5/3
b) \[\sqrt{19}\]
c) \[\frac{13}{3}\]
d) None of these
Explanation:
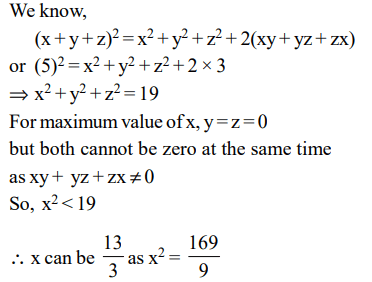
8. If \[x^{2}+5y^{2}+z^{2}=2y\left(2x+z\right)\] then which of the following statements are necessarily true?
I. x = 2 y
II. x = 2 z
III. 2x = z
a) Only I
b) Only II and III
c) Only I and II
d) None of these
Explanation:
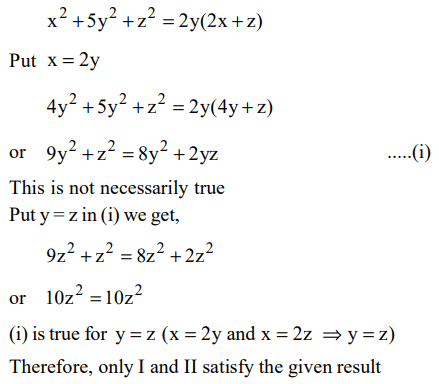
9. The number of real roots of the equation
\[\frac{A^{2}}{x}+\frac{B^{2}}{x-1}=1\] where A and B are real numbers not equal to zero simultaneously is
a) None
b) 1
c) 2
d) 1 or 2
Explanation:

10. If pqr = 1, the value of the expression \[\frac{1}{1+p+q^{-1}}+\frac{1}{1+q+r^{-1}}+\frac{1}{1+r+p^{-1}}\]
is equal to
a) p + q + r
b) \[\frac{1}{p+q+r}\]
c) 1
d) \[p^{-1}+q^{-1}+r^{-1}\]
Explanation: