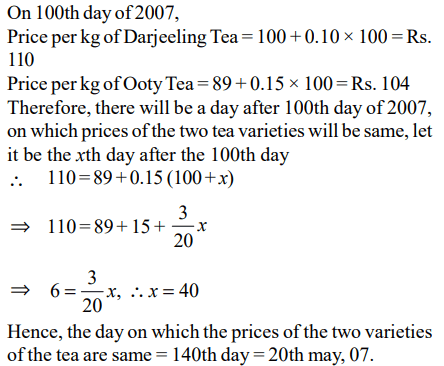1. Let \[y=\frac{1}{2+\frac{1}{3+\frac{1}{2+\frac{1}{3+.....}}}}\]
What is the value of y?
a) \[\frac{\sqrt{13}+3}{2}\]
b) \[\frac{\sqrt{13}-3}{2}\]
c) \[\frac{\sqrt{15}+3}{2}\]
d) \[\frac{\sqrt{15}-3}{2}\]
Explanation:
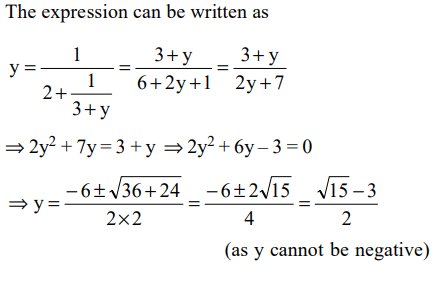
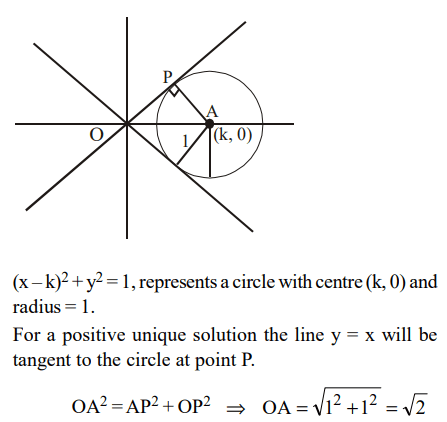
2. For which value of k does the following pair of equations yield a unique solution for x such that the solution
is positive?
\[x^{2}-y^{2}=0\]
\[\left(x-k\right)^{2}+y^{2}=1\]
a) 2
b) 0
c) \[\sqrt{2}\]
d) \[-\sqrt{2}\]
Explanation:
3. let \[x=\sqrt{4+\sqrt{4-\sqrt{4+\sqrt{4-.......infinity }}}}\]
Then x equals
a) 3
b) \[\left(\frac{\sqrt{13}-1}{2}\right)\]
c) \[\left(\frac{\sqrt{13}+1}{2}\right)\]
d) \[\sqrt{13}\]
Explanation:

4. A telecom service provider engages male and female operators for answering 1000 calls per day. A male operator can handle 40
calls per day whereas a female operator can handle 50 calls per day. The male and the female operators get a fixed wages of Rs.
250 and Rs. 300 per day respectively. In addition, a male operator gets Rs. 15 per call he answers and a female operator gets Rs.
10 per call she answer. To minimize the total cost, how many male operators should the service provider employ assuming he has
to employ more than 7 of the 12 female operators available for the job?
a) 15
b) 14
c) 12
d) 10
Explanation:

5. When you reverse the digits of the number 13, the number increases by 18. How many other two-digit numbers increase by 18
when their digits are reversed?
a) 5
b) 6
c) 7
d) 8
Explanation:

6. What values of x satisfy \[x^{2/3}+x^{1/3}-2\leq 0\]
a) \[-8\leq x\leq1\]
b) \[-1\leq x\leq8\]
c) 1 < x < 8
d) \[1\leq x\leq8\]
Explanation:
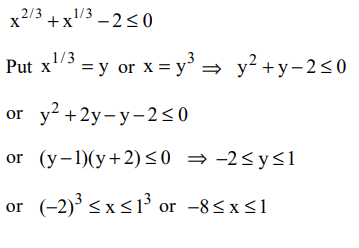
7. What are the values of x and y that satisfy both the equations?
\[2^{0.7x}.3^{-1.25y}=8\frac{\sqrt{6}}{27}\]
\[4^{0.3x}.9^{0.2y}=8.\left(81\right)^{1/5}\]
a) x = 2, y = 5
b) x = 2.5, y = 6
c) x = 3, y = 5
d) x = 5, y = 2
Explanation:
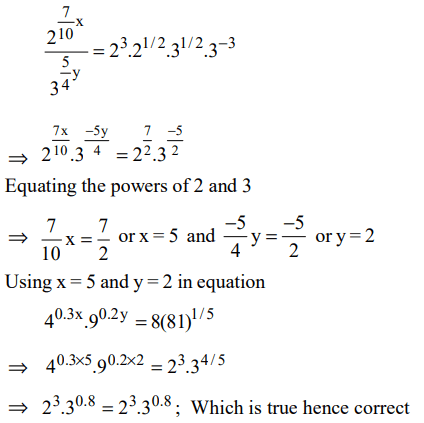
8. The number of solutions of the equation 2x + y = 40 where both x and y are
positive integers and \[x\leq y\]
a) 13
b) 14
c) 18
d) 20
Explanation:
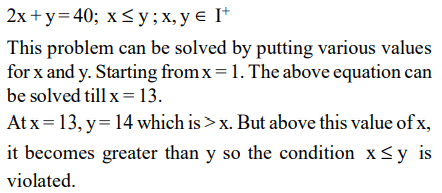
9. The sum of four consecutive two-digit odd numbers, when divided by 10, becomes a perfect square. Which of the following can
possibly be one of these four numbers?
a) 21
b) 25
c) 41
d) 67
Explanation:
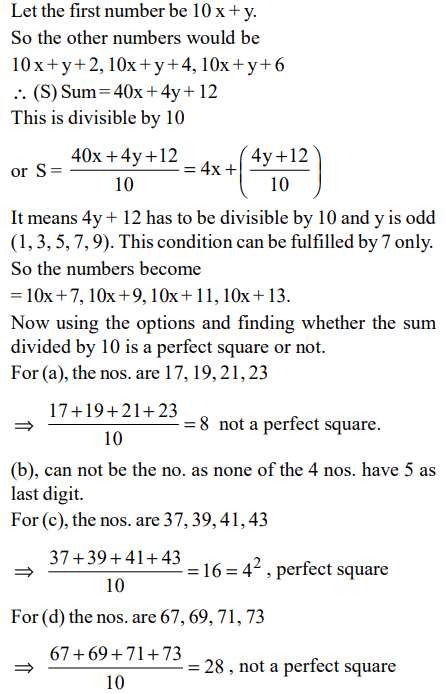
10. The price of Darjeeling tea (in rupees per kilogram) is 100 + 0.10n, on the \[n^{th}\] day of 2007 (n = 1, 2, ..., 100), and then remains
constant. On the other hand, the price of Ooty tea (in rupees per kilogram) is 89 + 0.15n, on the \[n^{th}\] day of 2007 (n = 1, 2, ..., 365).
On which date in 2007 will the prices of these two varieties of tea be equal?
a) June 30
b) May 21
c) April 11
d) May 20
Explanation: