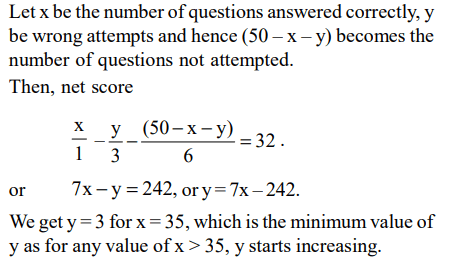1. A piece of string is 40 centimeters long. It is cut into three pieces. The longest piece is 3 times as long as the middle-sized piece
and the shortest piece is 23 centimeters shorter than the longest piece. Find the length of the shortest piece.
a) 17
b) 5
c) 4
d) 9
Explanation:
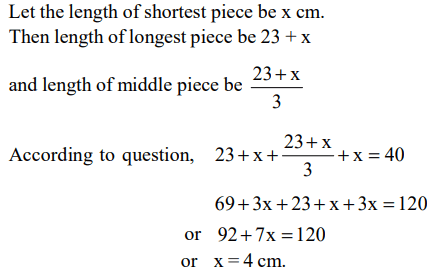
2. Three pieces of cakes of weight \[4\frac{1}{2}lbs,6\frac{3}{4}lbs\] and \[7\frac{1}{5}lbs\]
respectively are to be divided into parts of equal weights. Further,
each part must be as heavy as possible. If one such part is served to each guest, then what is the maximum number of guests that
could be entertained?
a) 54
b) 72
c) 20
d) None of these
Explanation:
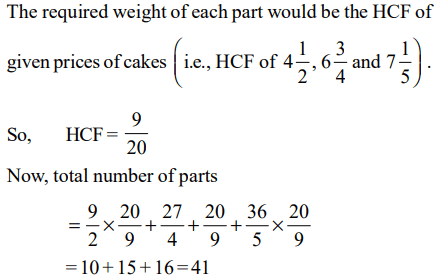
3. Which one of the following conditions must p, q and r satisfy so that the following system of linear simultaneous equations has
at least one solution, such that \[p+q+r\neq0\] ?
x + 2y -3z = p ; 2x + 6y -11z = q ; x - 2y + 7z = r
a) 5p - 2q - r = 0
b) 5p + 2q + r = 0
c) 5p + 2q - r = 0
d) 5p - 2q + r = 0
Explanation:

4. The number of non-negative real roots of \[2^{x}-x-1=0\] equals
a) 1.0
b) 1
c) 2
d) 3
Explanation: It is clear that the equation 2x – x – 1 = 0 is satisfied by x = 0 and 1 only.
For x > 1, f(x) = 2x – x – 1 start increasing.
Hence, there are 2 non-negative real roots.
5. Let a, b, c, d be four integers such that a + b + c + d = 4m + 1 where m is a positive integer. Given m, which one of the following
is necessarily true?
a) The minimum possible value of \[a^{2}+b^{2}+c^{2}+d^{2}\] is \[4m^{2}-2m+1\]
b) The minimum possible value of \[a^{2}+b^{2}+c^{2}+d^{2}\] is \[4m^{2}+2m+1\]
c) The maximum possible value of \[a^{2}+b^{2}+c^{2}+d^{2}\] is \[4m^{2}-2m+1\]
d) The maximum possible value of \[a^{2}+b^{2}+c^{2}+d^{2}\] is \[4m^{2}+2m+1\]
Explanation:
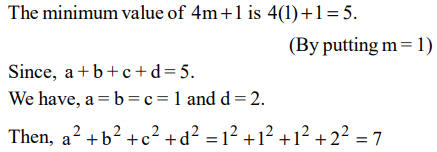
6. Let p and q be the roots of the quadratic equation \[x^{2}-\left(\alpha-2\right)x-\alpha-1=0\]
What is the minimum
possible value of \[p^{2}+q^{2}\] ?
a) 0
b) 3
c) 4
d) 5
Explanation:
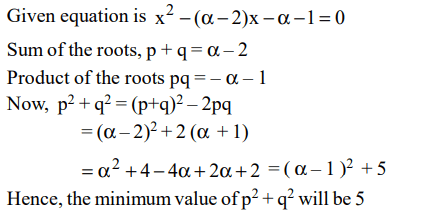
7. If the product of n positive real numbers is unity, then their sum is necessarily
a) a multiple of n
b) equal to \[n+\frac{1}{n}\]
c) never less than n
d) a positive integer
Explanation:
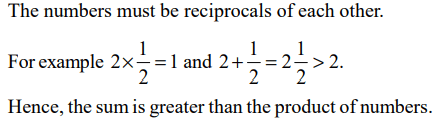
8.Given that\[-1\leq v\leq1 , -2\leq u\leq-0.5\] and \[-2\leq z \leq -0.5\] and \[w=\frac{vz}{u}\] , then which of the following is necessarily true?
a) \[-0.5\leq w\leq 2\]
b) \[-4\leq w\leq 4\]
c) \[-4\leq w\leq 2\]
d) \[-2\leq w\leq -0.5\]
Explanation:
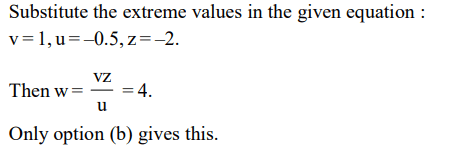
9. If x, y, z are distinct positive real numbers then \[\frac{x^{2}\left(y+z\right)+y^{2}\left(x+z\right)+z^{2}\left(x+y\right)}{xyz}\]
would be
a) greater than 4
b) greater than 5
c) greater than 6
d) None of the above
Explanation:
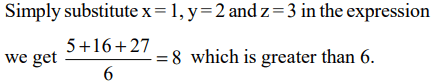
10. A test has 50 questions. A student scores 1 mark for a correct answer, –1/3 for a wrong answer, and 1/6 for not attempting a
question. If the net score of a student is 32, the number of questions answered wrongly by that student can not be less than
a) 6
b) 12
c) 3
d) 9
Explanation: